
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Джоуля-Ленца в дифференциальной формеСодержание книги
Поиск на нашем сайте
Количество тепла, выделяемое в элементарном объеме с сопротивлением R при прохождении тока I в течении времени dt:
29.
Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда. Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС) Представим стороннюю силу
где векторная величина
Интеграл, вычисленный для замкнутой цепи, дает ЭДС, действующую в этой цепи,
Последнее выражение дает самое общее определение ЭДС и пригодно для любых случаев. Если известно, какие силы вызывают движение зарядов в данном источнике, то всегда можно найти напряженность поля сторонних сил и вычислить ЭДС источника. Физическая природа электродвижущих сил в разных источниках весьма различна.
Рассмотрим пример. Пусть имеется металлический диск радиуса R (рис. 4.2), вращающийся с угловой скоростью
30.
Пусть на участке электрической цепи протекает постоянный ток I (рис. 6.7.). Напряжение U на концах этого участка численно равно работе, совершаемой электрическими силами при перемещении единичного положительного заряда по этому участку. Это следует из определения напряжения (см. 3.16).
Рис. 6.7. Отсюда работа A = q × U. За время t по участку будет перенесён заряд q = I × t и при этом будет совершена работа: A = q × U = U × I × t. (6.14) Это выражение работы электрического тока справедливо для любых проводников. Работа, совершаемая в единицу времени — мощность электрического тока:
В системе СИ мощность измеряется в ваттах: 1 Вт = 1 Дж/1 с = 1 В × 1 А. Работа электрического тока (6.14) может затрачиваться на нагревание проводника, совершение механической работы (электродвигатель) и на химическое действие тока при его течении через электролит (электролиз). Если химическое действие и механическая работа при течении тока не производятся, то вся работа электрического тока расходуется только на нагревание проводника: Q = A = U × I × t = I 2 × R × t. (6.15) Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме, позволяющая вычислить количество теплоты, выделяющейся в проводнике. Для того, чтобы характеризовать тепловой эффект тока в различных точках проводника, выделим в нём элементарный участок трубки тока (рис. 6.8.). Запишем для этого элемента закон Джоуля-Ленца: . Здесь мы использовали хорошо известные соотношения:
i = l E — закон Ома в дифференциальной форме; dV = dl × dS — объём выделенного элемента трубки тока.
Рис. 6.8. Разделив количество выделившейся теплоты dQ на время dt, получим тепловую мощность электрического тока:
Отнеся эту величину к объёму элемента трубки тока, придём к удельной тепловой мощности:
Перед нами закон Джоуля-Ленца в дифференциальной форме. Учитывая, что i = l E =
Подводя итог, ещё раз запишем формулы законов постоянного тока, рассмотренные на этой лекции. Закон Ома для участка цепи: в интегральной форме: в дифференциальной форме: Закон Джоуля-Ленца: в интегральной форме: Q = I 2 × R × t; в дифференциальной форме: Р уд = 31. Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любойэлектрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 780; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.66.242 (0.009 с.) |




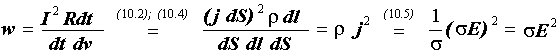

 , действующей в электрической цепи или на ее участке.
, действующей в электрической цепи или на ее участке. , действующую на заряд q, в виде
, действующую на заряд q, в виде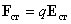 ,
, представляет напряженность поля сторонних сил. Тогда на участке цепи ЭДС равна
представляет напряженность поля сторонних сил. Тогда на участке цепи ЭДС равна .
. .
.
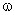 . Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности. Центростремительная сила
. Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности. Центростремительная сила  , где m - масса электрона; r - расстояние от оси диска. Эта сила действует на электрон и поэтому
, где m - масса электрона; r - расстояние от оси диска. Эта сила действует на электрон и поэтому 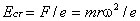 , возникающая ЭДС равна
, возникающая ЭДС равна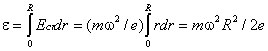 .
. .
. . (6.15)
. (6.15) — сопротивление участка;
— сопротивление участка; ,
,  .
.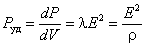 . (6.16)
. (6.16)
 , это выражение можно записать ещё и так:
, это выражение можно записать ещё и так: ,
,  .
. ;
; .
.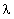 × Е 2=
× Е 2=  .
.


