Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Процессы установления тока при зарядке и разрядке конденсатора.Содержание книги
Поиск на нашем сайте ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи IR=U, где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем где q0 - начальный заряд конденсатора, е - основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t. Продифференцировав выражение (2) по времени, найдём закон изменения тока: где I0 - сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз. Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:
Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи: После разделения переменных уравнение примет вид: Проинтегрировав это уравнение с учётом начального условия q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим q = Анализ этого выражения показывает, что заряд приближается к своему максимальному значению, равному С Подставляя в формулу (4) функцию I(t) = dq/dt, получим Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dАист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW: dAист= dQ + dW, где dAист = Аист(t)= Q(t)= W(t) = 56. Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения). Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания Резонансная частота контура определяется так называемой формулой Томсона:
В цепи, содержащей индуктивность L и ёмкость С, могут возникать электрические колебания. Такая цепь называется колебательным контуром (рис. 4.1).
Рис. 4.1 Колебания в контуре можно вызвать либо зарядив конденсатор, либо вызвав в индуктивности ток (например включив магнитное поле). Поскольку активное сопротивление контура 57. Затухающие колебания. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Затухание механических колебаний вызывается главным образом трением. Затухание в электрических колебательных системах вызывается тепловыми потерями и потерями на излучение электромагнитных волн, а также тепловыми потерями в диэлектриках и ферромагнетиках вследствие электрического и магнитного гистерезиса. Закон затухания колебаний определяется свойствами колебательных систем. Система называется линейной, если параметры характеризующие те физические свойства системы, которые существенны для рассматриваемого процесса, не изменяются в ходе процесса. Линейные системы описываются линейными дифференциальными уравнениями. Различные по своей природе линейные системы описываются одинаковыми уравнениями, что позволяет осуществлять единый подход к изучению колебаний различной физической природы. Величину Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и (рис. 3.1):
где β– коэффициент затухания.
Рис. 3.1 Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз. Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. Генератор переменного тока. Генератор в основном состоит из проволочной катушки, вращающейся в однородном магнитном поле. Тот же самый результат может быть достигнут с помощью неподвижной катушки в магнитном поле, направление которого вращается по способу, описанному в предыдущей главе. Мы рассмотрим лишь первый случай. Пусть имеется круглая катушка из проволоки, которая может вращаться вокруг оси, проходящей вдоль одного из ее диаметров. И пусть эта катушка помещена в магнитное поле, перпендикулярное оси вращения (фиг. 17.6). Благодаря вращению катушки магнитный поток через нее будет меняться. Поэтому в цепи катушки появится э. д. с. Пусть S — площадь катушки, а θ — угол между магнитным полем и нормалью к плоскости катушки. Тогда поток через катушку равен
Если катушка вращается с постоянной угловой скоростью ω, то θ меняется со временем как ωt. Тогда э. д. с. Ε в катушке равна
Если мы выведем провода из генератора на некоторое расстояние от вращающейся катушки, в место, где магнитное поле равно нулю или хотя бы не меняется со временем, то ротор от Е в этой области будет равен нулю, и мы сможем определить электрический потенциал. В самом деле, если ток не уходит из генератора, то разность потенциалов V между двумя проводами будет равна э. д, с. вращающейся катушки, т. е.
Разность потенциалов в проводах меняется как sin ωt. Такая меняющаяся разность потенциалов называется переменным напряжением. Поскольку между проводами имеется электрическое поле, они должны быть электрически заряжены. Ясно, что э. д. с. генератора выталкивает лишние заряды в провода, пока их электрическое поле не становится достаточно сильным, чтобы в точности уравновесить силу индукции. Если посмотреть на генератор со стороны, то покажется, будто два провода электростатически заряжены до разности потенциалов V, а заряды как бы меняются со временем, создавая переменную разность потенциалов. Есть и еще одно отличие от того, что наблюдается в случае электростатики. Если присоединить генератор к внешней цепи, по которой может проходить ток, мы обнаружим, что э. д. с. не позволяет проводам разряжаться, а продолжает подпитывать их зарядами, когда из них уходит ток, стремясь сохранить на проводах одну и ту же разность потенциалов. Если генератор подключен к цепи, полное сопротивление которой равно R, ток в цепи будет пропорционален э. д. с. генератора и обратно пропорционален R. Поскольку э. д. с. синусоидально изменяется со временем, то и ток делает то же самое. Возникает переменный ток
Схема такой цепи приведена на фиг. 17.7.
59. Вынужденные электромагнитные колебания - незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.
Свободные незатухающие электромагнитные колебания можно получить в электрической цепи, состоящей из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R:
Такую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими.
Свободные незатухающие электромагнитные колебания можно получить только в идеализированном случае, когда можно пренебречь электрическим сопротивлением (R 0) контура. Такие свободные незатухающие колебания называют еще собственными электромагнитными колебаниями.
Можно доказать, что в колебательном контуре происходят гармонические колебания заряда, согласно закону:
где:q - мгновенное значение заряда конденсатора; q0 - амплитудное значение электрического заряда; w0 - собственная частота колебаний в контуре.
61 Цепи переменного тока. Ток, протекая через сопротивление (обычное, или активное), выделяет в нём тепловую энергию (эффект Джоуля). Возникает вопрос, каково должно быть соотношение между постоянным и переменным током, чтобы при протекании того и другого наблюдался одинаковый эффект. Решим эту задачу. Закон Джоуля гласит, что при фиксированном R выделяемое тепло Q пропорционально квадрату тока или напряжения:
В случае переменного тока тепло, выделяемое за время, равное периоду колебаний T выразится через интеграл:
Очевидно, что, если амплитуда переменного тока и величина постоянного тока будут соотноситься как
то выделяемое тепло в том и другом случае будет одинаково. Величину I называют эффективным, или действующим значением переменного тока; это, фактически, величина постоянного тока, оказывающего такое же действие, как переменный ток с амплитудой I0. Аналогично вводятся эффективные (или действующие) значения напряжения и э.д.с.:
Вычислим мощность, выделяемую на нагрузке (активном сопротивлении) при протекании переменного тока:
Cosj называют коэффициентом мощности, Закон Ома для переменного тока Протекающий по обмотке переменный ток создает магнитный поток. Этот магнитный поток точно так же, как и ток, изменяет свою силу и направление. При изменении магнитного потока по закону индукции в обмотке создается ЭДС (электродвижущая сила). Направление ЭДС противоположно полярности подаваемого напряжения. Это явление называется самоиндукцией.Самоиндукция в цепи переменного тока частично проявляется в сдвиге по фазе между током и напряжением и частично — в падении индуктивного напряжения. Сопротивление цепи переменного тока становится значительно выше рассчитанного или измеренного сопротивления этой же цепи постоянному току.Сдвиг по фазе между током и напряжением обозначается углом φ. Индуктивное сопротивление (реактивное) обозначается X, активное сопротиние — R, кажущееся сопротивление цепи или проводника — Z. Полное сопротивление (импеданс) вычисляется по формуле: Где:Z - полное сопротивление, ОмR - активное сопротивление, ОмЗакон Ома для цепи переменного тока:U=I*ZГде:U - напряжение, ВI - ток, АZ - полное сопротивление, Омпоэтому мощность P полная (произведение тока и напряжения) = 220*значение тока полное. Импеданс - полное электрическое сопротивление
64 Вектор плотности потока энергии электромагнитной волны (то, что в теории упругих волн называется вектором Умова) называется вектором Умова-Пойнтинга, или чаще просто вектором Пойнтинга Р:
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 2138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 и
и  , преобразуем закон Ома к виду
, преобразуем закон Ома к виду (1)
(1) , (2)
, (2) , (3)
, (3) (4)
(4) .
.
 , или после потенцирования
, или после потенцирования
 . (4)
. (4) , асимптотически при t ®?.
, асимптотически при t ®?. . (5)
. (5) . Тогда для произвольного момента времени t имеем:
. Тогда для произвольного момента времени t имеем: =
=  =С
=С 
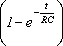 . (6)
. (6)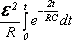 =С
=С  .(7)
.(7) =
=  .
.

 , полная энергия остаётся постоянной. Если энергия конденсатора равна нулю, то энергия магнитного поля максимальна, и наоборот.
, полная энергия остаётся постоянной. Если энергия конденсатора равна нулю, то энергия магнитного поля максимальна, и наоборот. называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину
называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину  обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,
обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,
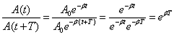 ,
,
 ;
; .
. отсюда
отсюда 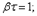
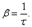

 ;
;  ;
; .
. Представим себе., что оба конца катушки выведены на внешнюю цепь с помощью каких-нибудь скользящих контактов.
Представим себе., что оба конца катушки выведены на внешнюю цепь с помощью каких-нибудь скользящих контактов.
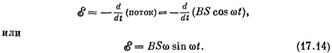




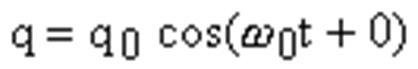







 Под U мы понимаем напряжение на клеммах генератора. Мощность в цепи переменного тока, как видим, зависит от времени; величину N называют ещё мгновенной мощностью. Практически более важной величиной является среднее за период значение мгновенной мощности; её называют активной мощностью Р:
Под U мы понимаем напряжение на клеммах генератора. Мощность в цепи переменного тока, как видим, зависит от времени; величину N называют ещё мгновенной мощностью. Практически более важной величиной является среднее за период значение мгновенной мощности; её называют активной мощностью Р: