
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательно-параллельное (смешанное) соединение конденсаторовСодержание книги
Поиск на нашем сайте
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов. На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов. При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид: 1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов. 2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость. 3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов. 4. Рассчитывают емкость полученной схемы. Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
19.
Энергия взаимодействия электрических зарядов 1. При перемещении электрических зарядов силы кулонова взаимодействия между ними совершают определенную работу А. Очевидно, что мы должны приписать всякой системе зарядов определенную энергию взаимодействия, за счет убыли которой и совершается работа А:
Энергию взаимодействия зарядов W мы часто будем называть просто электрической энергией. 2. Исходя из (15.1), подсчитаем прежде всего энергию двух точечных зарядов е\ и е2, находящихся на расстоянии R12 друг от друга. Всякое изменение взаимного расстояния зарядов сопровождается работой электрических сил. Предположим, например, что заряд е2 остается неподвижным, тогда как заряд е\ перемещается в поле заряда е2 из точки Pi в точку Р[. Если ф1 — = е2/R12 — потенциал поля заряда е2 в точке Р\, а ф + dф\ — в точке Р[, то работа А электрических сил при этом перемещении равна А — —е1 dф1, откуда А = —dW = —е1 dф1, и, следовательно.
Ввиду того, что наблюдению доступны лишь изменения энергии, а не ее абсолютная величина, мы для простоты опустили здесь аддитивную постоянную интегрирования, от взаимного расположения зарядов не зависящую (ср. сказанное о собственной энергии зарядов в конце следующего параграфа). В связи с этим единственно учитываемая нами переменная часть энергии W может принимать и отрицательные значения х). К тому же выражению для W мы пришли бы, конечно, рассматривая перемещение заряда в2 в поле неподвижного заряда е\ или, наконец, одновременное перемещение обоих зарядов. Обозначая через ф2 потенциал заряда е\ в точке, занимаемой зарядом е2 (ф2 = ei/R12), можно вместо (15.2) написать
Удобнее же всего взаимную электрическую энергию зарядов г\ и ег записать в симметричной форме:
Чтобы определить энергию системы п точечных зарядов ег (г = 1, 2,..., п), мы, очевидно, для каждой пары этих зарядов должны написать выражения типа (15.2) или (15.3) и сложить все эти выражения. Собирая затем все члены суммы, в которые входит сомножителем убедимся, что коэффициент при который мы обозначим через фк/2, будет равен
где фkl — потенциал заряда ег в точке, занимаемой зарядом ек. Выражение в скобках представляет собой, очевидно, значение потенциала поля всей системы зарядов в точке, занимаемой зарядом eк, или, вернее, потенциал всей системы зарядов, кроме самого заряда ек (потенциал фкк заряда ек в занимаемой им самим точке поля в выражение для фк не входит, да и вообще физического значения не имеет, ибо обращается в бесконечность). Итак, взаимная энергия системы п зарядов равна
где фk — потенциал поля в точке, занимаемой зарядом ек- Чтобы выяснить зависимость W от взаимного расстояния зарядов, воспользуемся формулой (8.6), которая в наших теперешних обозначениях запишется следующим образом:
где суммирование должно быть распространено по всем индексам г, кроме i = к. Внося это в (15.4), получим
Формулу эту можно, конечно, получить и непосредственно из выражения (15.2) взаимной энергии пары зарядов. Появление же коэффициента 1/2 перед знаком суммы объясняется тем, что в эту сумму энергия каждой пары зарядов входит дважды; так, например, в ней встретится как член e2е1/R21-, так и равный ему член e2е1/R21- 3. Как и всегда, при пользовании представлением о точечных зарядах нужно помнить, что приведенные формулы могут применяться лишь в тех случаях, когда заряды системы отделены друг от друга расстояниями, достаточно большими по сравнению с размерами этих зарядов. Чтобы освободиться от этого ограничения, перейдем к рассмотрению объемных и поверхностных зарядов. Разлагая систему этих зарядов на совокупность элементарных зарядов pdV и adS, применяя к последним формулу (15 4) и переходя от суммирования к интегрированию, получим
гдеф — потенциал поля всех объемных и поверхностных зарядов в элементе объема dV или на элементе поверхности dS. Хотя и может казаться, что уравнение (15.6) представляет собой только видоизменение уравнения (15.4), соответствующее замене представления о точечных зарядах представлением о зарядах объемных и поверхностных, однако в действительности уравнения эти разнятся по своему содержанию. Именно, в следующем параграфе мы покажем, что формула (15.6) выражает полную энергию системы электрических зарядов, тогда как формула (15.4) не учитывает так называемой собственной энергии зарядов eк. Пример 1. Энергия точечного заряда и диполя во внешнем электрическом поле. Часто приходится рассматривать работу электрических сил при перемещениях некоторого заряда е в заданном «внешнем» поле других зарядов, остающихся при этом неподвижными. Взаимная энергия этих «внешних» зарядов (а также и собственная энергия их и заряда е — см. § 16) остается при этом неизменной; переменная же часть энергии поля, за счет которой совершается работа электрических сил, носит название энергии заряда е во внешнем поле. Она равна, очевидно,
где ф — потенциал внешнего поля в точке, занимаемой зарядом е. Формула (15.2) представляет собой частный случай формулы (15.7). Если во внешнем поле находятся два заряда, е > 0 и е' = — —е, образующие диполь бесконечно малой длины I (см. с. 47), то энергия этих зарядов во внешнем поле равна
где ф и ф' — потенциалы внешнего поля в полюсах диполя. Но с точностью до величин второго порядка малости
Стало быть,
где р — момент диполя [см. уравнение (8.9)], а Е — напряженность внешнего поля в месте расположения диполя. Конечно, в этом выражении не учитывается взаимная энергия зарядов диполя, которая изменяется лишь при изменении длины диполя I. Пример 2. Непосредственный подсчет электрической энергии заряженного конденсатора. До зарядки конденсатора каждая из его обкладок электрически нейтральна, т. е. содержит в себе равное количество положительного и отрицательного электричества. Будем заряжать конденсатор, отнимая электричество определенного знака от одной из его обкладок и перенося его на другую. Практически это осуществляется, как известно, соединением пластин конденсатора проводом, в который включен источник ЭДС, например гальванический элемент; элемент этот перекачивает электричество из одной обкладки в другую, пока разность потенциалов обкладок не достигнет известного значения. Пусть в некоторый момент этого процесса потенциалы обкладок достигли значений ф1 иф2, причем ф2 > ф1- Перенос следующей порции электричества de с первой обкладки на вторую сопровождается отрицательной работой сил электрического поля, равной dA = de(фi — ф2) (см. § 8). Очевидно, что «внешние» по отношению к полю конденсатора ЭДС элемента преодолевающие силы этого поля совершат при этом положительную работу dAmm = -dA = de(ф2 - ф1). Воспользовавшись формулой (9.1), получаем
где С — емкость конденсатора. Общая же работа, затраченная на доведение заряда пластин от нуля, скажем, до е', будет, очевидно, равна
Работа эта совершается за счет уменьшения химической энергии гальванического элемента и переходит в энергию электрического поля заряженного конденсатора. Обозначая эту последнюю энергию через W и принимая во внимание (9.1), получим ряд следующих выражений для W:
где штрих у е нами опущен 20. Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен
При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:
Применяя соотношение
Для заряженного конденсатора разность потенциалов (напряжение) равна
21.
|
||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 930; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.88.18 (0.006 с.) |


















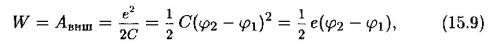
 , а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная
, а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная  . Но потенциал электростатического поля данного проводника в бесконечности равен нулю
. Но потенциал электростатического поля данного проводника в бесконечности равен нулю  . Тогда
. Тогда


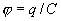 , можно получить следующие выражения для потенциальной энергии W:
, можно получить следующие выражения для потенциальной энергии W:
 поэтому соотношение для полной энергии его электростатического поля имеют вид
поэтому соотношение для полной энергии его электростатического поля имеют вид



