Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия. Потенциальная энергия. Закон сохранения энергии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением. Потенциальная энергия Момент силы. Уравнение моментов. Момент силы F относительно неподвижной точки О называется физическая величина определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку приложения силы, на силу F: М =[ rF ], модуль момента: М=Fr Sina =F l; a- угол между r и F. Моментом силы относительно неподвижной оси z называется скалярная величина Мz равная проекции на эту ось вектора момента силы. Момент импульса. Закон сохранения момента импульса. Моментом импульса (количества движения) матер-ой точки A относительно неподвижной точки О наз. физ. величина, определяемая векторным произведением: где r — радиус-вектор, проведенный из точки О в A; p = mv — импульс материальной точки. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц. Закон сохранения момента импульса: момент импульса замкнутой системы, взятый относительно любой точки инерциальной системы отсчета, не изменяется при любых процессах, происходящих внутри данной системы ?????19.Основное уравнение динамики вращательного движения. Его различные формы. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.d L /dt= M – еще одна форма уравнения (закона) динамики вращательного движения твердого тела. Момент инерции. Примеры вычисления моментов инерции твердых тел. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Измеряется: кг·м².Обозначается: I или J. Примеры:
Теорема Штейнера. Примеры ее применения. Если известен момент инерции тела относительно оси проходящей ч/з его центр масс то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси проходящей ч/з центр масс С тела, сложенной с произведением массы m тела на квадрат расстояния а между осями: J= Jc + ma2. Пример: Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.232.137 (0.009 с.) |

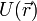 — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является Джоуль. Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
— скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является Джоуль. Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.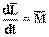 - уравнение моментов: скорость изменения момента импульса частицы относительно некоторой точки
- уравнение моментов: скорость изменения момента импульса частицы относительно некоторой точки 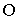 во времени в выбранной системе отсчета равно моменту равнодействующей силы относительно той же точки.
во времени в выбранной системе отсчета равно моменту равнодействующей силы относительно той же точки.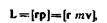
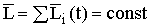 .
.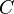 ) равен
) равен 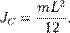 Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен 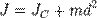 где
где 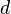 — расстояние между искомой осью и осью
— расстояние между искомой осью и осью 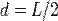 :
: