
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетического уровня на другой. Какие переходыСодержание книги
Поиск на нашем сайте Соответствуют поглощению энергии. 1. 3,4,6 2. 1,2,5 3. 1,2,3,4,5,6 Туннельный эффект Закончите определение Туннельный эффект-это явление, при котором квантовая частица проходит через потенциальный барьер при А) E < Uо Б) E > Uо В) E = Uо Где E – кинетическая энергия частицы Uо – высота потенциального барьера Волны де Бройля Вычислить дебройлевскую длину волны электрона имеющую кинетическую Энергию 25 ЭВ А) 2,4×10-9 М Б) 1,2×10-9 М В) 0,24×10-9 М Г)0,12×10-9 М Где h = 6,62 ×10-34 mе = 9,1×10-31 кг qе = 1,6×10-19 Кл 3) Каков импульс протона с дебройлевской длиной волны 2,86×10-12 м (масса протона mp = 1,6×10-27 кг) А) 3,7×10-22 Б) 1,4×10-22 В) 2,3×10-22 Соотношение неопределенностей Гейзенберга Оценить неопределенность скорости электрона в атоме водорода, полагая размер атома водорода Dx = 0,10 нм А) 1,16×106 м/с Б) 0,116×106 м/с В) 7,27×106 м/с Г) 0,727×106 м/с Атомная физика Сколько квантов с различной энергией может испустить атом водорода, если его электрон находится на третьем энергетическом уровне. А) 1 Б) 2 В) 3 Г) 4
Вопрос 1 (Строение атома водорода) Какие значения могут принимать орбитальное квантовое число L при заданном главном квантовом числе n? 1. Целые числа 1,2... n-1 2. Целые числа 0,1... n-1 3. Целые числа 0,1... 2n 4. Целые числа 1,2... 2n 5. Целые числа n,n+1... 2n Ответ Как показывает теория, состояние электрона в атоме определяется 4 квантовыми числами: главным квантовым, орбитальным квантовым, магнитным квантовым и спиновым числами, причем первые три квантовых числа взаимосвязаны между собой. Связь между орбитальным квантовым числом L и главным квантовым числом n следующая – L может принимать значения от нуля до (n-1). Вопрос 2 (Соотношения неопределенностей) Квантовая частица проходит сквозь потенциальный барьер конечной высоты. Чем объясняется прохождение частицы сквозь потенциальный барьер? Неприменимостью закона сохранения энергии для квантовой механики Тем, что сумма потенциальной и кинетической энергии вследствие соотношения неопределенностей неоднозначно определяет полную энергию частицы Тем, что при прохождении потенциальной ямы частица приобретает дополнительную энергию 4. Среди вышеперечисленных вариантов нет правильного Ответ Для частицы, рассматриваемой с точки зрения квантовой механики, не существуют одновременно величина координаты и величина скорости, поэтому нельзя утверждать, что частица будет обладать какой-либо скоростью до прохождения ямы (находясь “левее” ямы) или после ее прохождения (находясь “правее” ямы), и как следствие – нельзя утверждать, что в квантовой механике полная энергия частицы представима в виде суммы кинетической и потенциальной энергий (т.е. определенна однозначно). В квантовой механике в любой момент времени можно определить только усредненные значения кинетической и потенциальной энергий во всех точках, в которых волновая функция отлична от нуля. Вопрос 3 (Уравнение Шредингера) Свободная частица в квантовой механике описывается соответствующей плоской монохроматической волной Де Бройля. Остается ли постоянной вероятность обнаружить такую свободную частицу в произвольной точке пространства?
1. Да 2. Да, при условии выбора однородной области пространства 3. Нет 4. Среди вышеперечисленных ответов нет наиболее полного Ответ Вероятность обнаружить такую свободную частицу в любой точке пространства постоянна независимо от свойств пространства.
Вопрос 4 (Уравнение Шредингера)
Согласно принципу соответствия Бора при больших квантовых числах наблюдается соответствие наблюдаемых явлений законам классической физики. Пусть Wn – дискретное значение энергии, соответствующее n-ому квантовому числу (достаточно большому). Определить, какое утверждение будет справедливым
1. а)(Wn+1-Wn)>>Wn б)Энергетические уровни квазинепрерывны 2. а)(Wn+1-Wn)<<Wn б)Энергетические уровни квазинепрерывны 3. а)(Wn+1-Wn)<<Wn б)Энергетические уровни не квазинепрерывны 4. а)(Wn+1-Wn)>>Wn б)Энергетические уровни не квазинепрерывны 5. а)(Wn+1-Wn)=Wn б)Энергетические уровни квазинепрерывны 6. а)(Wn+1-Wn)=Wn б)Энергетические уровни не квазинепрерывны
Ответ
Соответствие классическим законам физики с точки зрения строения энергетических уровней определяется их квазинепрерывностью. В свою очередь это определяет то свойство, что разность между значениями энергий соседних уровней будет значительно меньше значения энергии Wn. Из этих соображений правильным будет ответ 2.
Вопрос 5 (Соотношения неопределенностей)
Положив неопределенность координаты электрона в электронно-лучевой трубке монитора равной 10-4 м, а его скорость – порядка 106 м/с, определить, какие свойства электрона как частицы стоит использовать для его описания?
1. Только корпускулярные свойства 2. Корпускулярные и волновые свойства в одинаковой мере 3. Только волновые свойства 4. Среди перечисленных ответов нет правильного
Ответ
Из соотношения Гейзенберга мы можем грубо оценить неопределенность скорости электрона: Очевидно, что заданная неопределенность скорости много меньше самой скорости, поэтому волновые свойства электрона можно не учитывать, а учитывать только корпускулярные свойства Уравнения Шредингера. 1. Определить минимально вероятную энергию Е для квантовой частицы, находящейся в бесконечно глубокой потенциальной яме шириной а: 1. Е = 0; 2. Е = h2/32ma2; 3. Е = h2/2ma2; 4. E = h2/8ma2. 2. В бесконечно глубокой потенциальной яме шириной L находится электрон. Вычислить вероятность w нахождения электрона на первом энергетическом уровне в интервале (А, В):
L/4 L/4
|
1. w = 0;
2. w = 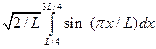 ;
;
3. w = 2/L 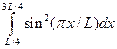 ;
;
4. w =2/L 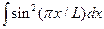 .
.
3. Квантовая частица находиться в бесконечно глубокой потенциальной яме. Сравнить разность соседних энергетических уровней часицы ∆Е = Еn+1 – En с энергией частицы Еn, при n =:
1) ∆Е = En ;
2) ∆Е = (2n+1)/n2En ;
3) ∆Е = n2/(2n+1)En
4) ∆Е << En.
4. Квантовая частица массы m находиться в бесконечно глубокой потенциальной яме шириной а. Какую энергию Е надо сообщить чтобы перевести ее с третьего энергетического уровня на пятый:
1. Е = h2/4ma2;
2. E = ћ2p2/ma2;
3. E = 2h2/ma2;
4. E = h2/2ma2.
5. Квантовая частица массы m находится в трехмерной кубической бесконечно глубокой потенциальной яме с абсолютно непроницаемыми стенками. Ребро куба равно a. Найти энергию Е шестого уровня:
1. Е = 7 ћ2p2 /ma2;
2. E = 6 ћ2p2 /ma2;
3. E = 5 ћ2p2 /ma2.
Уравнения Шредингера.
1. Квантовая частица находится в бесконечно глубокой потенциальной яме шириной а. В каких точках нахождения электрона на первом энергетическом уровне y - функция максимальна:
a) x = 0; c) x = a/2; e) x = a;
b) x = a/3; d) x = 2a/3;
1. a, b;
2. a, b, c;
3. a, c, e;
4. c;
5. a, e;
B,d.
2. Квантовая частица находится в бесконечно глубокой потенциальной яме шириной а. В каких точках третьего энергетического уровня частица находиться не может:
a) x = 0; c) x = a/2; e) x = a;
b) x = a/3; d) x = 2a/3;
1. a, c, e;
2. a, e;
3. b, d;
4. a, b, d, e.
3. Квантовая частица находится в бесконечно глубокой потенциальной яме шириной а. Определить вероятность w того, что частица, находящаяся на втором энергетическом уровне, будет обнаружена в интервале (a/3 £ x £ 2a/3):
w = 0;
w = 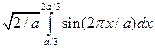 ;
;
w = 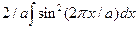 ;
;
w = 2/a  .
.
4. Квантовая частица находится в бесконечно глубокой потенциальной яме шириной а. В каких точках интервала (0, а) плотность вероятности нахождения частицы на первом и втором энергетическом уровнях одинакова?
1. a/4, 3a/4;
2. a/3, 2a/3;
3. a/2;
4. a/5, 4a/5;
5. Электрон наталкивается на потенциальный барьер конечной высоты. При каком значении энергии Е электрона он не пройдет через потенциальный барьер высотой U0:
1. E < U0 ;
2. E = U0 ;
3. E > U0 ;
4. нет верных ответов.
Как записывается уравнение Шредингера для стационарных состояний:
1. ΔΨ- 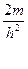 (E-U)Ψ=0
(E-U)Ψ=0
2. ΔΨ+ 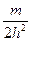 (E-U)Ψ=0
(E-U)Ψ=0
3. ΔΨ+ 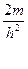 (E-U)Ψ=0
(E-U)Ψ=0
4. ΔΨ- 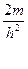 (E+U)Ψ=0
(E+U)Ψ=0
5. ΔΨ+ 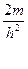 (E+)Ψ=0
(E+)Ψ=0
2) Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью, ширина которой а=2 мкм. Определить скорость электронов (она одинакова для всех частиц), если известно, что на экране, отстоящем от щели на l=50см, ширина главного дифракционного максимума Δх=80 мкм.
1. 4.5∙106 м/c
2. 2.9 ∙106 м/c
3. 3.9∙106 м/c
4. 4.6∙106 м/c
5. 4.1∙106 м/c
Найти скорость электрона, который находится в возбуждённом атоме водорода при n=2
1. 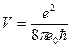
2. 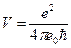
3. 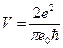
4. 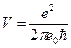
4) Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном, энергия которого ε=15 эВ. Определить скорость V электрона за пределами атома:
1. 0,7∙106 м/с
2. 1.2∙106 м/с
3. 0,7∙105 м/с
4. 1.2∙105 м/с
5) Фотон с энергией ε=12,12 эВ, поглощённый атомом водорода, находящегося в основном состоянии, переводит атом в возбуждённое состояние. Определить главное квантовое число n, соответствующее этому состоянию:
1. n=3 2. n=2 3.n=4
Раздел 1 
|
| Поделиться: |


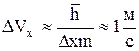

 U
U


 A B X
A B X


