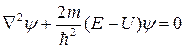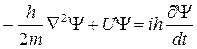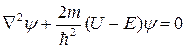Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исходя из соотношения неопределённостей оценить минимальную кинетическую энергию электрона, движущегося По стационарной орбите атома водородаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1) 1эВ; 2) 2эВ; 3) 3эВ; 4) 4эВ. Раздел 2 Электрон в атоме находиться в f-состоянии. Определите момент импульса электрона. 1) 4ħ; 2) 2,2ħ; 3) 3ħ; 4) 3,46ħ. 3. Электрон находиться в прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы L=0,2 нм, энергия электрона En=37,7эВ. Определить номер энергетического уровня. 1) 1; 2) 2; 3) 3; 4) 4. 5) 4. Y- функция некоторой частицы в потенциальном поле имеет вид Y=(А/r)e-r/a, где r – расстояние этой частицы до силового центра, а – некоторая постоянная. Используя условие нормировки вероятностей, запишите Y-функцию частицы в явном виде. 1) 2) 3) 4) Раздел 3 Используя теорию Бора для атома водорода, определите скорость движения электрона по первой боровской орбите. 1) 2) 3) 4) Раздел 1 Исходя из соотношения неопределённостей оценить минимальную кинетическую энергию электрона, движущегося по стационарной орбите атома водорода 1) 1эВ; 2) 2эВ; 3) 3эВ; 4) 4эВ. Раздел 2 Электрон в атоме находиться в f-состоянии. Определите момент импульса электрона. 1) 4ħ; 2) 2,2ħ; 3) 3ħ; 4) 3,46ħ. 8. Электрон находиться в прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы L=0,2 нм, энергия электрона En=37,7эВ. Определить номер энергетического уровня. 1) 1; 2) 2; 3) 3; 4) 4. 5) 9. Y- функция некоторой частицы в потенциальном поле имеет вид Y=(А/r)e-r/a, где r – расстояние этой частицы до силового центра, а – некоторая постоянная. Используя условие нормировки вероятностей, запишите Y-функцию частицы в явном виде. 1) 2) 3) 4) Раздел 3 Используя теорию Бора для атома водорода, определите скорость движения электрона по первой боровской орбите. 1) 2) 3) 4) Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью шириной a = 2 мкм. Определить положение 2ого дифракционного минимума на экране, отстающем от щели на расстояние l = 50 см. Скорость всех электронов одинакова и равна 1. 2. 3. 4. Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью шириной a = 2 мкм. Во сколько раз отличается ширина 1ого дифракционного максимума b1 от центрального дифракционного максимума b ( 1. 1 2. 2 3. 0.5 4. 0.4 2с Пучок электронов встречает на своем пути потенциальный барьер высотой U = 27 эВ. Определить энергию электронов E, если известно, что коэффициент пропускания волн Де Бройля D = 8/9. Известно, что U < E. 1. 36 эВ ЭВ ЭВ ЭВ 2с Определить значение орбитального момента импульса PQ электрона в возбужденном атоме водорода при максимальном орбитальном квантовом числе l, если энергия возбуждения E = -12.9 эВ. 1. 2. 3. 4. Частица находится в возбужденном (n = 4) состоянии в одномерном потенциальном ящике шириной l с абсолютно непроницаемыми стенками. В какой из областей A(0 <= x <= l/3) и B(2/3 <= x <= l) вероятность пребывания электрона больше. 1. A > B 2. A<B 3. A=B Недостаточно данных 1. Определить длину волны λ спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома изменилась на ∆Ε=20эВ. 1. 62нм Нм Нм Нм 2. Определить импульс и энергию электрона, если длина волны λ=1,2нм. 1. p=3,5∙1023 E=3,32∙1019 2. p=3,5∙10-23 E=3,32∙10-19 3. p=5,5∙10-25 E=1,66∙10-19 4. p=5,5∙1025 E=1,66∙1019 3. Заряженная частица, ускоренная разностью потенциалов U=600В, имеет длину волны де Бройля λ=1,3пм. Принимая заряд этой частицы равным заряду электрона, определить ее массу. 1. 1,7∙10-25 2. 2,7∙10-27 3. 1,35∙10-27 4. 3,2∙10-25 4. На дифракционную решетку с периодом d нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Дифракционный максимум в спектре k-го порядка, наблюдаемый под углом φ, соответствует одной из линий серии Лаймана. Определите главное квантовое число, соответствующее энергетическому уровню, с которого произошел переход. 1. 2. 3. 4. 5. ψ-Функция некоторой частицы, находящейся в потенциальном поле, имеет вид 1. 2. 3. 4. 1. Как выглядят формулы уравнений: а) временного уравнения Шредингера б) стационарного уравнения Шредингера (Ñ2 – оператор Лапласа) А. Б. В. Г. Ответы: 1. а) А б) Б 2. а) В б) Б 3. а) В б) Г 4. а) А б) Г 2. Какой оператор имеет следующий вид: Ответы: Оператор координаты Оператор проекции импульса 3. Оператор кинетической энергии Оператор полной энергии
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1058; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

 ;
;
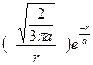

 ;
; ;
; ;
; .
.





 ). Скорость всех электронов одинакова и равна
). Скорость всех электронов одинакова и равна 

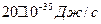




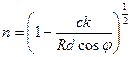
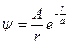 , где r – расстояние этой частицы до силового центра; a – некоторая постоянная. Определите явный вид ψ-функции частицы.
, где r – расстояние этой частицы до силового центра; a – некоторая постоянная. Определите явный вид ψ-функции частицы.