
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Консервативная сила равна градиенту потенциальной энергии, взятому с обратным знаком.Содержание книги
Поиск на нашем сайте
Градиентом скалярной величины называется вектор, характеризующий быстроту изменения этой величины в пространстве. Этот вектор направлен в сторону наиболее быстрого возрастания величины и численно равен скорости этого возрастания. Основное свойство гравитационного поля: на всякую материальную точку массой m, внесенную в это поле, действует сила тяготения F пропорциональная массе m:
где Следовательно, для гравитационного поля:
Следовательно:
Это связь напряженности с потенциалом. В каждой точке поля тяготения вектор напряженности направлен в сторону наиболее быстрого уменьшения потенциала.
Закон сохранения механической энергии Рассмотрим замкнутую систему материальных точек, между которыми действуют только консервативные силы. Согласно второму закону Ньютона:
Пусть за время dt все точки совершат перемещения
Сложим эти уравнения:
При этом:
а
причем
Следовательно:
Таким образом (24) можно записать в виде:
следовательно:
Закон сохранения механической энергии: Полная механическая энергия замкнутой системы не меняется с течением времени. Для незамкнутой системы тел изменение полной механической энергии равно работе внешних сил:
Если в системе действуют силы трения, то их работу нужно учитывать также как и работу внешних сил. Поскольку работа сил трения отрицательна, то при наличии сил трения полная механическая энергия убывает (превращается в другие виды энергии). Закон сохранения энергии один из фундаментальных универсальных законов природы, справедливый как для макроскопических тел, так и для элементарных частиц. В теоретической физике доказывается, что этот закон вытекает из однородности времени, то есть независимости физических законов от выбора отсчета времени.
Применение законов сохранения энергии и Импульса к столкновениям Процессы столкновения делятся на упругие и неупругие в соответствии с характером изменения внутренней энергии частиц при их взаимодействии. Если внутренняя энергия частиц при этом изменяется, то столкновение называется неупругим, если не изменяется, то столкновение называют упругим. Иногда говорят об абсолютно упругом столкновении, чтобы подчеркнуть, что внутренняя энергия сталкивающихся частиц абсолютно точно неизменна. Говорят также и об абсолютно неупругом столкновении, если в конечном состоянии вся энергия превратилась во внутреннюю. 1. Упругое столкновение. Пусть две частицы массами m1 и m2 движутся в одном направлении, но с разными скоростями, причем V2 > V1 (рис. 12).
Решая совместно уравнения системы (27), найдем скорости U1 и U2 частиц после их столкновения:
Анализируя уравнения (28) и (29), рассмотрим два случая: а) массы частиц одинаковы ( б) масса первой частицы много больше массы второй (m1>>m2), причем она неподвижна (V1=0). Эта ситуация может произойти, например, при столкновении частицы массой m2 с неподвижной стенкой. В таком случает после упругого удара массы m2 стенка останется неподвижной (U1=0), а частица m2 поменяет скорость на противоположную (U2=-V2). 2. Неупругое столкновение. Если частицы массами m1 и m2 претерпевают неупругое центральное столкновение, то их скорости после удара одинаковы, поэтому закон сохранения импульса будет иметь вид:
Скорость
Поскольку при таком столкновении механическая энергия меняется, легко рассчитать ее изменение:
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.202 (0.005 с.) |

 , (20)
, (20) - напряженность поля тяготения, его силовая характеристика.
- напряженность поля тяготения, его силовая характеристика.
 ,
,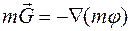 .
. . (21)
. (21) (22)
(22) . Умножим каждое уравнение системы скалярно на соответствующее перемещение
. Умножим каждое уравнение системы скалярно на соответствующее перемещение  :
: (23)
(23) (24)
(24) ,
,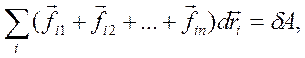
 ,
, .
.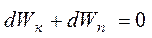 ,
, (25)
(25) (26)
(26) Тогда, в случае их упругого центрального столкновения, можно записать закон сохранения импульса и закон сохранения механической энергии:
Тогда, в случае их упругого центрального столкновения, можно записать закон сохранения импульса и закон сохранения механической энергии: . (27)
. (27) , (28)
, (28) (29)
(29) ). В этом случае легко убедиться, что после столкновения они просто обменяются скоростями
). В этом случае легко убедиться, что после столкновения они просто обменяются скоростями  и
и  ;
; . (30)
. (30) после столкновения:
после столкновения: (31)
(31) (32)
(32)


