Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле кругового токаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
что линии магнитной индукции поля кругового тока не являются правильными окружностями, они замыкаются, обходя проводник, по которому идет ток. Направление линий магнитной индукции можно определить с помощью правила правого винта (правило буравчика): если головку винта вращать в направлении тока в проводнике, то поступательное движение острия винта покажет направление магнитной индукции в центре кругового тока. Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.
Циркуляцией магнитного поля
где Соответствующий интеграл для электрического поля
Магнитное поле не является потенциальным, оно, как было показано выше, является соленоидальным. Поэтому следует ожидать, что циркуляция магнитного поля вдоль замкнутого контура в общем случае отлична от нуля. Чтобы найти ее величину, выполним сначала некоторые вспомогательные действия. Поле соленоида и тороидаСоленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник. Тороид можно рассматривать как длинный соленоид, свернутый в кольцо внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю). Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, охватывающему все N витков, согласно (4.12) равна: Магнитное поле внутри тороида, так же, как в соленоиде, однородно, сосредоточено внутри; вне тороида магнитное поле, создаваемое круговыми токами тороида, равно нулю. Величина магнитного поля в тороиде определяется выражением причем длина тороида l берется по средней длине тороида (среднему диаметру).
Магни́тный пото́к — поток
где α — угол между вектором магнитной индукции и нормалью к плоскости площади В соответствии с теоремой Гаусса для магнитной индукции поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
Или, в дифференциальной форме — дивергенция магнитного поля равна нулю:
Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.131 (0.009 с.) |

 где I ток в контуре гамма контур, по которому идет интегрирование r0 произвольная точка
где I ток в контуре гамма контур, по которому идет интегрирование r0 произвольная точка вдоль замкнутого контура l называется интеграл:
вдоль замкнутого контура l называется интеграл: ,
, - проекция вектора
- проекция вектора  в электростатике, как мы знаем, равен нулю, что отражает свойство потенциальности электростатического поля:
в электростатике, как мы знаем, равен нулю, что отражает свойство потенциальности электростатического поля: .
. .
. где μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно
где μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно как интеграл вектора магнитной индукции
как интеграл вектора магнитной индукции  через конечную поверхность
через конечную поверхность 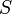 . Определяется через интеграл по поверхности
. Определяется через интеграл по поверхности Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:
Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади: