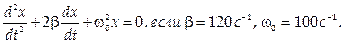Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения мкт. Идеальный газ.Содержание книги Поиск на нашем сайте
Основные положения МКТ. Идеальный газ. 1. К одному из основных положений молекулярно–кинетической теории следует отнести следующее высказывание: 1) молекулы вещества могут находиться только в поступательном и вращательном движениях; 2) молекулы вещества взаимодействуют между собой; 3) размерами молекул можно пренебречь. 2. Между молекулами действуют 1) силы притяжения; 2) силы отталкивания; 3) силы притяжения и отталкивания 3. Идеальным называется газ, для которого можно пренебречь 1) размерами молекул; 2) взаимодействием молекул; 3) и размерами и взаимодействием. 4. Какой газ ближе к идеальному? 1) с большим давлением и малой температурой; 2) с малым давлением и малой температурой; 3) с малым давлением и большой температурой. 5. Молекулы газов участвуют 1) только в поступательном движении; 2) в поступательном и вращательном движении; 3) в поступательном, вращательном и колебательном движении. 6. Молекулы газов при столкновениях 1) обмениваются энергией между собой; 2) обмениваются ускорениями движений; 3) подчиняются закону абсолютно неупругого удара. 7. При столкновении со стенкой сосуда, молекула передаёт стенке импульс, равный (в проекции на ось х) 1) 8. При ударе о стенку сосуда молекула изменяет свой импульс на величину
Основные определения (давление, плотность количество вещества, константы и размерность) 9. 1 моль вещества имеет столько же молекул, сколько их в 1) 1 г водорода; 2) 1 г углерода; 3) 12 г углерода. 10. Давление газа это 1) сила тяжести молекул, действующая на единицу площади поверхности сосуда; 2) сила давления молекул, действующая на единицу площади поверхности сосуда; 3) оба варианта верны. 11. Один паскаль – это давление, которое 1) создаётся силою в 1 ньютон, которая действует нормально на площадку площадью в 1 см2; 2) создаётся силою в 1 ньютон, которая действует нормально на площадку площадью в 1 м2; 3) создаётся силою в 1 Кг, которая действует нормально на площадку площадью в 1 см2.
12. Концентрация молекул это 1) число молекул в 2) число молекул в 3) число молекул в 13. Число Авогадро определяет 1) число молекул в 2) число молекул в
3) число молекул в 14. Число Авогадро равно 1) 15. Масса одной молекулы кислорода равна (относительная атомная масса кислорода равна 16) 1) 16. Универсальная газовая постоянная равна 1) 17. Количество вещества можно найти по формуле 1) 18. Количество вещества можно найти по формуле 1) 19. Сколько моль содержится в 5 граммах кислорода? (Относительная атомная масса кислорода 16). 1) 20. Сколько моль содержится в 96 граммах кислорода? (Относительная атомная масса кислорода 16). 1) 21. Молярная масса смеси газов находится по формуле 1) 22. Какова молярная масса смеси, состоящей из 5 молей гелия и 2 молей водорода? (Молярная масса гелия 1) 23. Найти молярную массу смеси, состоящей из 9 г водяных паров и 11 г углекислого газа? (Молярная масса воды 1)
Длина свободного пробега 1. Эффективный диаметр молекул – это 1) расстояние, пройденное молекулой между двумя столкновениями; 2) расстояние, на которое сближаются центры молекул при столкновении; 3) кубический корень из объёма, приходящегося на одну молекулу газа в сосуде. 2. Длина свободного пробега молекулы – это 1) среднее расстояние между молекулами; 2) среднее расстояние, которое проходит молекула между двумя столкновениями; 3) среднее расстояние взаимодействия молекул. 3. Длина свободного пробега зависит от давления согласно рисунку
4. Длина свободного пробега молекулы зависит от давления как показано на рисунке
5. При данной температуре длина свободного пробега молекул 1) пропорциональна давлению; 2) обратно пропорциональна давлению; 3) обратно пропорциональна корню из давления. 6. При данной температуре длина свободного пробега молекул 1) пропорциональна концентрации молекул; 2) обратно пропорциональна концентрации молекул; 3) обратно пропорциональна корню из концентрации молекул. 9. Термодинамика. Определения. 1-е начало. Простые вопросы. 1. Количество теплоты – это 1) средняя кинетическая энергия молекул; 2) мера превращения энергии хаотического или направленного движения в энергию хаотического движения; 3) мера внутренней энергии тела. 2. Внутренняя энергия – это
1) средняя кинетическая энергия теплового движения молекул; 2) тепловая энергия, получаемая системой при теплопередаче; 3) сумма кинетической и потенциальной энергии всех молекул системы. 3. Работа в термодинамике – это 1) мера превращения энергии хаотического или направленного движения в энергию хаотического движения; 2) мера превращения энергии хаотического или направленного движения в энергию направленного движения; 3) мера изменения внутренней энергии тела. 4. Число степеней свободы молекулы равно 1) числу независимых координат, полностью описывающих положение молекулы; 2) числу атомов в молекуле, умноженному на 3; 3) числу координатных осей, которые можно провести через каждые два атома в молекуле. 5. На каждую степень свободы молекулы приходится энергия 1) 6. Внутренняя энергия идеального газа определяется по формуле 1) 7. Элементарная работа, совершаемая газом, определяется по формуле 1) 8. Работа, совершаемая газом, определяется по формуле 1) 9. Изменение внутренней энергии 1) зависит от вида процесса, совершаемого газом; 2) не зависит от вида процесса, совершаемого газом; 3) зависит от изменения объёма газа. 10. Определение внутренней энергии как суммы кинетических энергий всех молекул справедливо для 1) идеального газа; 2) всех газов; 3) всех тел. 11. Работа, совершаемая газом 1) зависит от вида процесса, совершаемого газом; 2) не зависит от вида процесса, совершаемого газом; 3) равна 12. Внутренняя энергия идеального газа зависит от температуры согласно графику
13. Первое начало термодинамики можно записать так 1) 14. Первое начало термодинамики можно сформулировать так 1) работа, совершенная системой равна сумме количества теплоты, переданного системе и изменения внутренней энергии системы; 2) количество теплоты, переданное системе, идёт на повышение её внутренней энергии и совершение над системой работы; 3) количество теплоты, переданное системе, идёт на совершение системой работы и изменение её внутренней энергии. 15. Работа при изобарном процессе (площадь под кривой) правильно изображена на графике
16. Для изотермического процесса первое начало термодинамики выглядит так 1) 17. Для изотермического процесса справедливо 1) 18. Для изохорного процесса первое начало термодинамики выглядит так 1) 19. Для изохорного процесса справедливо 1) 20. Работа при изобарном процессе равна 1) 21. Для изохорного процесса 1) работа, совершенная системой всегда больше изменения внутренней энергии; 2) работа, совершенная системой всегда меньше изменения внутренней энергии; 3) работа, совершенная системой всегда равна изменению внутренней энергии. 22. Для изохорного процесса 1) количество теплоты, переданное системе, всегда больше изменения внутренней энергии системы; 2) количество теплоты, переданное системе, всегда меньше изменения внутренней энергии системы; 3) количество теплоты, переданное системе, всегда равно изменению внутренней энергии системы. 23. Для изотермического процесса 1) количество теплоты, переданное системе, всегда больше работы, совершенной системой; 2) количество теплоты, переданное системе, всегда меньше работы, совершенной системой; 3) количество теплоты, переданное системе, всегда равно работе, совершенной системой.
Тепловые машины 1. КПД тепловой машины находится по формуле 1) 2. КПД тепловой машины находится по формуле 1) 3. КПД тепловой машины находится по формуле 1) 4. Выражение для КПД 1) только для тепловой машины, работающей по циклу Карно; 2) только для тепловой машины, работающей на идеальном газе; 3) для любой тепловой машины. 5. Выражение для КПД 1) только для тепловой машины, работающей по циклу Карно; 2) только для тепловой машины, работающей на идеальном газе; 3) для любой тепловой машины. 6. КПД цикла Карно находится по формуле 1) 7. Для любой тепловой машины справедливо соотношение 1) 8. Для идеальной тепловой машины, работающей по циклу Карно 1) выполненная работа меньше теплоты, переданной нагревателем; 2) выполненная работа больше теплоты, переданной нагревателем; 3) выполненная работа равна теплоте, переданной нагревателем. 9. Для любой тепловой машины 1) выполненная работа меньше теплоты, переданной нагревателем; 2) выполненная работа меньше теплоты, полученной холодильником; 3) выполненная работа меньше теплоты, переданной нагревателем и полученной холодильником. 10. Цикл Карно состоит из 1) двух изохор и двух адиабат; 2) двух изотерм и двух адиабат; 3) двух изобар и двух адиабат. 11. Тепловая машина 1/3 тепла, полученного от нагревателя, отдаёт холодильнику. Чему равен КПД такой машины? 1) 0,33; 2) 0,45; 3) 0,66. 12. Идеальная тепловая машина, работающая по циклу Карно1/3 тепла, полученного от нагревателя отдаёт холодильнику. Найти температуру холодильника, если температура нагревателя равна 270С. 1) 100 К; 2) 133 К; 3) 166 К. 13. КПД тепловой машины, получающей от нагревателя 450 Дж тепла, и отдающей холодильнику 140 Дж равен 1) 0,31; 2) 0,46; 3) 0,69. 14. КПД идеальной тепловой машины, имеющей температуру нагревателя 4500С, и холодильника 600С равен 1) 0,36; 2) 0,46; 3) 0,64. 15. Идеальная тепловая машина, работающая по циклу Карно, имеет КПД 30%. Найти температуру холодильника, если температура нагревателя равна 3000С. 1) 372 К; 2) 401 К; 3) 472 К. 16. Что выгоднее для повышения КПД идеальной тепловой машины 1) повысить температуру нагревателя на 200; 2) понизить температуру холодильника на 200; 3) одинаково. 17. КПД идеальной тепловой машины 1) равен 1; 2) определяется температурами нагревателя и холодильника; 3) определяется трением в машине. 18. Цикл Карно правильно показан на рисунке
19. Цикл Карно правильно показан на рисунке
20. Цикл Карно правильно показан на рисунке
Задачи 100. Амплитуда вынужденных колебаний зависит от частоты внешней периодически действующей силы ω по формуле:
Исходя из этой формулы, покажите, что резонансная частота определяется выражением: . 101. Гармоническое колебание совершается по закону 1). 102. Гармоническое колебание совершается по закону 1). 103. Гармоническое колебание совершается по закону 1). 104. Гармоническое колебание совершается по закону 1). 105. Гармоническое колебание совершается по закону 1). 106. Пружинный маятник массой m=100 г совершает гармонические колебания с частотой ω0 = 30 рад/с. Чему равна жёсткость пружины? 1. 90 Н/м; 2. 30 Н/м; 3. 45 Н/м. 107. На пружине жёсткостью к= 1 кН/м укреплён груз массой m= 1 кг. Чему равен период колебаний такого пружинного маятника? 1. 6.28 с; 2. 1 с; 3. 3.14 с. 108. Определить возвращающую силу F в момент времени t=1/8 c точки массой m=20 г, совершающей гармонические колебания согласно уравнению 1. -1.43 Н; 2. 1.43 Н; 3. 0. 109. Определить потенциальную энергию Wp в момент времени t=1/8 c точки массой m=20 г, совершающей гармонические колебания согласно уравнению 1. 0.214 Дж; 2. 0.107 Дж. 3. 0. 110. Определить кинетическую энергию Wк в момент времени t=1/8 c точки массой m=20 г, совершающей гармонические колебания согласно уравнению 1. 0.214 Дж; 2. 0.107 Дж. 3. 0. 111. Определить полную энергию точки массой m=20 г, совершающей гармонические колебания согласно уравнению 1. 3.14·10 -2 Дж; 2. 6.31·102 Дж; 3. 5.14·102 Дж;
112. Определить максимальную скорость 1. 6·10 -2 м/с; 2. 3·10 -2 м/с; 3. 1.5·10 -2 м/с. 113. Определить максимальное по модулю ускорение 1. 0.18 м/с2; 2. 0.36 м/с2; 3. 0.72 м/с2. 114. Материальная точка совершает гармонические колебания согласно уравнению 1. 0.13 с. 2. 0.52 с. 3. 0.26 с. 115. Материальная точка совершает гармонические колебания согласно уравнению 1. 0.13 с. 2. 0.52 с. 3. 0.26 с. 116. На пружине жёсткостью к= 4 кН/м укреплён груз массой m= 1 кг. Напишите уравнение колебаний такого пружинного маятника, если амплитуда колебаний А= 2 см. 1). x=0.02 cos2t; 2) x=0.02 cos4t; 3) x=0.02 cost. 117. Материальная точка совершает гармонические колебания согласно уравнению 1. 0.13 с. 2. 0.52 с. 3. 0.39 с. 118. Материальная точка совершает гармонические колебания с периодом Т=4 с. В некоторый момент времени смещение максимально. Через какой промежуток времени Δt скорость достигнет максимального значения? 1) 1 c; 2) 2 c; 3) 4 с. 119. Материальная точка совершает гармонические колебания с периодом Т=4 с. В некоторый момент времени скорость максимальна. Через какой промежуток времени Δt ускорение достигнет максимального значения?
1) 1 c; 2) 2 c; 3) 4 с. 120. Материальная точка совершает гармонические колебания с периодом Т=4 с. В некоторый момент времени ускорение максимально. Через какой промежуток времени Δt скорост ь достигнет максимального значения? 1) 1 c; 2) 2 c; 3) 4 с. 121. Материальная точка совершает гармонические колебания с амплитудой А. При каких значениях смещения х скорость максимальна? 1) х = 0; 2) х = А; 3) х = А/2. 122. Материальная точка совершает гармонические колебания с амплитудой А. При каких значениях смещения х ускорение максимально? 1) х = 0; 2) х = А; 3) х = А/2. 123. Материальная точка совершает гармонические колебания с амплитудой А. При каких значениях смещения х ускорение и скорость одновременно достигают максимального значения? 1) х = 0; 2) х = А; 3) Такое состояние не реализуется. 124. Материальная точка совершает гармонические колебания с периодом Т=4 с.. В некоторый момент времени кинетическая энергия максимальна. Через какой промежуток времени потенциальная энергия достигнет максимального значения? 1) 2 c; 2) 1 c; 3) 4 с. 125. Найти максимальную кинетическую энергию материальной точки массой m=2 г, совершающей гармонические колебания с амплитудой А= 4 см и частотой 1) 0.04 мДж; 2) 3 .16 мДж; 3) 1.58 мДж. 126. Точка совершает гармонические колебания. В некоторый момент времени смещение точки x=5 см и модуль ускорения │ a │ = 80 см/с2. Найти циклическую частоту колебаний ω. 1) 4 с-1; 2) 16 с-1; 3) 8 с-1. 127. Точка совершает гармонические колебания c частотой ω = 10 с-1. В некоторый момент времени смещение точки x=4 см и модуль скорости │ v │ = 30 см/с2. Найти амплитуду колебаний. Указание: воспользуйтесь тождеством 1) 3 см; 2) 5 см; 3) 4 см. 128. Материальная точка массой m= 100 г совершает гармонические колебания, уравнение которых имеет вид x=A·sinωt, где А=5 см, ω =2с-1. В какой момент времени (ближайший к началу отсчёта) возвращающая сила F= –10-2 Н? 1) π/3; 2) π/6; 3) π/12. 129. Два гармонических колебания, направленных вдоль одной прямой, имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз складываемых колебаний. 1) 600; 2) 900; 3) 1200. 130. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: 1. 131. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: 1) 6 см; 2) 4 см; 3) 132. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: 1) 1 см; 2) 7 см; 3) 5 см. 133. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: 1) 31 см; 2) 7 см; 3) 1 см. 134. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: 1) 5 см; 2) 5.9 см; 3) 7 см. 135. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: 1) 136. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: 1) 137. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями:
138. Найти линейную частоту колебаний груза массой 400 г, подвешенного к пружине жёсткостью 160 Н/м. 1) 3 .2 Гц; 2) 20 Гц; 3) 400 Гц. 139. Найти массу груза, который на пружине с жёсткостью 250 Н/м делает 20 колебаний за 16 с. 1) 3 кг; 2) 4 кг; 3) 5 кг. 140. Во сколько раз изменится частота колебаний автомобиля на рессорах после принятия груза, равного массе порожнего автомобиля? 1) увеличится в 141. Шарик, подвешенный на тонкой нерастяжимой нити, совершал колебания с периодом Т. Во сколько раз изменится период колебаний, если отрезать ¾ длины нити и подвесить на оставшуюся часть тот же шарик. 1) увеличится в 2 раза; 2) не изменится; 3) уменьшится в 2 раза. 142. Груз массой 1 кг, подвешенный к пружине с жёсткостью 100Н/м, совершает колебания с амплитудой 10 см. Написать уравнение 1) 143. Чему равно ускорение свободного падения, если математический маятник длиной 80 см совершил за 3 мин 100 колебаний? 1) 9.81 м/с2; 2) 9.74 м/с2;3) 9.78 м/с2. 144. Как относятся длины математических маятников, если за одно и то же время один из них совершает 10, а второй 30 колебаний? 1) 3:1; 2) 1:3; 3) 9 :1. 145. За одно и то же время один математический маятник делает 50 колебаний, а второй 30. Найти их длины, если один из них на 32 см короче другого. 1) l1=50 cм, l2 =18 cм; 2) l1=60 cм, l2 =28 cм; 3 l1=40 cм, l2 =8 cм. 146. Груз совершает колебания на пружине жёсткостью k = 250 Н/м. Амплитуда колебаний A = 15 см. Найти полную механическую энергию колебаний. 1) 1.4 Дж; 2) 2.8 Дж; 3) 4.2 Дж. 147. Во сколько раз изменилась полная механическая энергия математического маятника при уменьшении длины в 3 раза и увеличении амплитуды в 2 раза? 1) увеличилась в 12 раз; 2) уменьшилась в 12 раз; увеличилась в 6 раз. 148.Груз, подвешенный на пружине с жёсткостью k = 1кН/м, колеблется с амплитудой A=2 см. Найти кинетическую Wk и потенциальную Wp энергию при фазе π/3 рад. Указание: для однозначности ответа выразите уравнение движения через косинус. 1) Wk=50 мДж, Wp=150 мДж; 2) Wk=150 мДж, Wp=50 мДж; 3) Wk=120мДж, Wp=80 мДж; 149. Пружинный маятник вывели из положения равновесия и отпустили. Через какое время (в долях периода) кинетическая энергия колеблющегося тела будет равна потенциальной энергии пружины? 1) Т/2; 2) Т/4; 3) Т/8. 150. Частица массой m = 0.01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы W=0.1 мДж. Определить амплитуду А колебаний. 1) 45 мм; 2) 54 мм; 3) 24 мм. 151. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых: 1) 152. Определить частоту 1) 0.76 Гц; 2) 0.98 Гц; 3) 0.67 Гц. 153. Определить частоту 1) 0.51 Гц; 2) 0.61 Гц; 3) 0.71 Гц; 154. Определить частоту 1) 1.46 Гц; 2) 3.86 Гц; 3) 2.26 Гц. 155. Определить частоту 1) 1.56 Гц; 2) 1.46 Гц; 3) 1.36 Гц. 156. Определить частоту 1) 0.92 Гц; 2) 0.62 Гц; 3) 0.32 Гц. 157. Через время, равное периоду колебаний Т = 2 с, амплитуда затухающих колебаний уменьшилась в 2 раза. Определить логарифмический декремент затухания λ и коэффициент затухания β. 1) λ= 0.301, β=0.15 с- 1; 2) λ= 0.693, β=0.346 с-1;3) λ= 1, β=0.5 с-1. 158. Амплитуда затухающих колебаний убывает по закону 1) 0.25; 2) 0.5; 3) 0.75. 159. Амплитуда затухающих колебаний убывает по закону 1) λ =0.5, Q=6.28; 2) λ =0.25, Q=12.56; 3) λ =0.75, Q=4.19. 160. Затухающие колебания описываются уравнением 1) λ =0.5, Q=6.28; 2) λ =1.05, Q=3; 3) λ =0.75, Q=4.19. 161. Затухающие колебания описываются уравнением 1) λ =0.5, Q=6.28; 2) λ =0.17, Q=18.5; 3) λ =1.26, Q=2.5. 162. В некоторый момент времени полная механическая энергия системы, совершающей затухающие колебания, была W1= 2 мДж. Через время, равное периоду колебаний, энергия системы стала равной W2= 1.95 мДж. Определить добротность системы Q и логарифмический коэффициент затухания λ. 1) Q =40, λ =7.85· 10-2; 2) Q =50, λ = 6.28· 10-2;3) Q =80, λ =3.92 · 10-2. 163. Внутри системы массой m=1 кг, совершающей затухающие колебания, действуют квазиупругая сила 1) 2) 3)
164. Внутри системы массой m=2 кг, совершающей затухающие колебания, действуют квазиупругая сила 1) 2) 3) 165. Внутри системы массой m=0.2 кг, совершающей затухающие колебания, действуют квазиупругая сила 1) 2) 3) 166. Какой вид будет иметь решение дифференциального уравнения затухающих колебаний 1) а; 2) б; 3) в.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.34 (0.016 с.) |

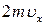 ; 2)
; 2)  ; 3)
; 3)  .
. , равную
, равную
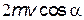 ;
2)
;
2)  ;
3) 0.
;
3) 0.
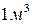 вещества;
вещества;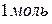 вещества;
вещества; вещества;
вещества; вещества;
вещества; ; 2)
; 2)  ; 3).
; 3). 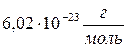
 ; 2)
; 2)  ; 3)
; 3)  .
. 2)
2)  3)
3) 
 2)
2) 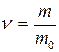 ; 3) обе формулы верны.
; 3) обе формулы верны.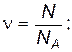 3) обе формулы верны.
3) обе формулы верны. ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 2)
; 2)  ; 3)
; 3)  .
. , а водорода
, а водорода  )
) ; 2)
; 2)  ; 3)
; 3)  .
. , а углекислого газа
, а углекислого газа  )
) ; 2)
; 2)  ; 3)
; 3) 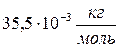 .
.


 ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3) 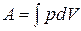 .
. .
.
 ; 2)
; 2)  ; 3)
; 3)  .
.
 ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2) 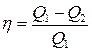 ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. ; 3)
; 3)  .
.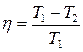 справедливо
справедливо ; 2)
; 2)  ; 3)
; 3)  ; 2)
; 2)  ; 3)
; 3)  .
.



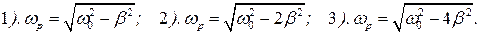
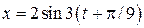 . Чему равна скорость в момент времени t=0?
. Чему равна скорость в момент времени t=0? ; 2). 3/2; 3). 2.
; 2). 3/2; 3). 2.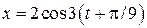 . Чему равна скорость в момент времени t=0?
. Чему равна скорость в момент времени t=0? ; 3). 2.
; 3). 2. ; 2). 3/2; 3).
; 2). 3/2; 3).  .
. . Чему равен период колебаний?
. Чему равен период колебаний? ; 2).
; 2).  ; 3). 2.
; 3). 2. . Чему равен период колебаний?
. Чему равен период колебаний? ; 2).
; 2).  ; 3). 1.
; 3). 1. , где А=15 см, ω=4p с-1.
, где А=15 см, ω=4p с-1. материальной точки, совершающей гармонические колебания согласно уравнению
материальной точки, совершающей гармонические колебания согласно уравнению  материальной точки, совершающей гармонические колебания согласно уравнению
материальной точки, совершающей гармонические колебания согласно уравнению 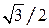 значения амплитуды?
значения амплитуды? значения амплитуды?
значения амплитуды?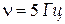 .
. .
.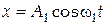 и
и  , где А1= 4 см, ω1 = π с-1; А2= 8 см, ω2=π с-1, τ=1 с. Найти уравнение траектории.
, где А1= 4 см, ω1 = π с-1; А2= 8 см, ω2=π с-1, τ=1 с. Найти уравнение траектории. .
. и
и 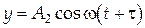 , где А1= 4 см, А2 = 8 см, ω = π с-1, τ = 1 с. Найти результирующую амплитуду колебаний.
, где А1= 4 см, А2 = 8 см, ω = π с-1, τ = 1 с. Найти результирующую амплитуду колебаний. см.
см. ; 2)
; 2)  ; 3)
; 3)  .
. . Найти траекторию движения точки.
. Найти траекторию движения точки.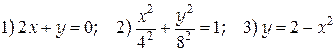 .
. раза; 2) не изменится; 3) уменьшится в
раза; 2) не изменится; 3) уменьшится в  движения груза.
движения груза.
 , где А1=1 см, ω1=π с-1; А2=2 см, ω1=π/2 с-1. Найтиуравнение траектории точки.
, где А1=1 см, ω1=π с-1; А2=2 см, ω1=π/2 с-1. Найтиуравнение траектории точки. 2)
2)  3)
3) 
 гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости. Справка: собственный момент диска
гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости. Справка: собственный момент диска  .
.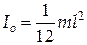 .
. .
. . Частота колебаний
. Частота колебаний  , где β=2 с-1, ω=12 с-1. Определить логарифмический декремент затухания λ и добротность Q.
, где β=2 с-1, ω=12 с-1. Определить логарифмический декремент затухания λ и добротность Q. и сила сопротивления
и сила сопротивления  , где
, где  . Напишите дифференциальное уравнение затухающих колебаний.
. Напишите дифференциальное уравнение затухающих колебаний.
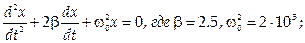

 . Напишите дифференциальное уравнение затухающих колебаний.
. Напишите дифференциальное уравнение затухающих колебаний.


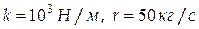 . Напишите дифференциальное уравнение затухающих колебаний.
. Напишите дифференциальное уравнение затухающих колебаний.