
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложные задачи на газовые законыСодержание книги Поиск на нашем сайте
1. Определить давление газа после его сжатия в цилиндре двигателя внутреннего сгорания, если его температура возросла в 3 раза, объём уменьшился в 30 раз, а первоначальное давление было 1 атм. 1) 2. Плотность идеального газа можно рассчитать по формуле 1) 3. Плотность водорода при давлении 1) 4. Как изменилось давление газа, если объём увеличился в 2 раза, а температура снизилась в 3 раза? 1) увеличилось в 1,5 раза; 2) уменьшилось в 6 раз; 3) уменьшилось в 1,5 раза. 5. Найти плотность водорода при нормальных условиях ( 1) 6. Найти плотность кислорода при давлении 1) 7. Плотность некоторого газа при температуре 100С и давлении 1) 8. При нормальном атмосферном давлении ( 1) 9. При совершении некоторого процесса объём уменьшился в 2 раза, а давление увеличилось в 5 раз. Во сколько раз изменилась температура газа? 1) уменьшилась в 10 раз; 2) увеличилась в 10 раз; 3) увеличилась в 2.5 раза. 10. В баллоне находится газ при температуре 1) 11. В баллоне при температуре 270 К находится 2 кг газа. Какую массу газа нужно удалить из баллона, чтобы после нагревания до температуры 300 К давление осталось тем же? 1) 12. Какое давление рабочей смеси установится в цилиндре двигателя, если в конце такта сжатия температура повышается от 500С до 2500С, а объём уменьшается от 0,75 л до 0,12 л. Начальное давление 1) 13. Газ в сосуде находится под давлением 1) 14. Определить молярную массу газа, если при температуре 154 К и давлении 1) 15. Два сосуда одинаковой вместимости заполнены кислородом. В одном сосуде давление 1) 16. Баллон ёмкостью 40 л наполнили углекислым газом массой 1,98 кг (молярная масса углекислого газа
1) 320 К; 2) 420 К; 3) 520 К. 17. Задан график процессов в координатах 18.
На каком графике правильно изображен цикл, нарисованный в координатах P, V? 19. Заданный круговой цикл перерисован в координатах
20. На сколько изменилась температура газа при изохорном процессе, если давление увеличилось в 2 раза (начальная температура была 1) увеличилась на 2) уменьшилась на 3) увеличилась на
5.Основные определения статистики Максвелла 1. Распределение Максвелла – это распределение частиц по 1) потенциальным энергиям; 2) скоростям; 3) полной механической энергии. 2. Функция распределения Максвелла определяет 1) абсолютное число частиц, имеющих скорости в интервале от 2) абсолютное число частиц, имеющих энергии в интервале от 3) относительное число частиц, имеющих скорости в интервале от 3. Функция распределения Максвелла определяет 1) абсолютное число частиц, имеющих скорости в интервале от 2) относительное число частиц, имеющих скорости в интервале от 3) относительное число частиц, имеющих скорости в единичном интервале. 4. Функция распределения Максвелла определяет 1) абсолютное число частиц, имеющих скорость 2) относительное число частиц, имеющих скорость 3) относительное число частиц, имеющих скорость в интервале от 5. Функция распределения Максвелла определяет 1) абсолютное число частиц, имеющих скорости в интервале от 2) число частиц в единичном объёме, имеющих скорости в интервале от 3) относительное число частиц, имеющих скорости в интервале от 6. Функция распределения Максвелла определяется выражением 1) 7. При данной температуре наибольшее число молекул имеют скорость вблизи 1) средней скорости; 2) среднеквадратичной скорости; 3) наиболее вероятной скорости. 8. Наиболее вероятная скорость молекул это 1) среднее значение всех скоростей молекул; 2) среднее значение модулей всех скоростей молекул; 3) скорость, близкую к которой имеет максимальное количество молекул. 9. Среднеквадратичная скорость это
1) квадрат от средней скорости молекул; 2) корень квадратный от среднего квадрата скоростей молекул; 3) наиболее вероятная скорость в квадрате. 10. Средняя скорость молекул это 1) скорость, которую имеют большинство молекул; 2) среднее значение модулей скоростей всех молекул; 3) оба утверждения верны. 11. Среднеквадратичная скорость молекул газа при данном давлении зависит от 1) температуры; 2) объёма; 3) оба утверждения верны. 12. В данном объёме при данной температуре Т скорости молекул 1) одинаковы; 2) лежат в интервале 3) могут быть любыми.
13. Среднеквадратичная скорость молекул кислорода на уровне моря была 500 м/с. Какой стала среднеквадратичная скорость на высоте 5 км? (Считать температуру постоянной). 1) 372 м/с 2) 500 м/с; 3) 813 м/с.
14. График функции распределения Максвелла изображён на рисунке
15. Функция распределения Максвелла для двух температур указана правильно на рисунке
16. а) б) в)
17. Площадь заштрихованной фигуры на графике
1) абсолютное число частиц, имеющих скорости в интервале от 2) число частиц в единичном объёме, имеющих скорости в интервале от 3) относительное число частиц, имеющих скорости в интервале от 18. Условие нормирования функции распределения Максвелла выглядит как 1) 19. Площадь под кривой от функции распределения Максвелла равна 1) единице; 2) числу молекул газа; 3) числу молекул в единице объёма газа. 20. При увеличении температуры площадь под кривой функции распределения Максвелла 1) увеличивается; 2) уменьшается; 3) остаётся постоянной. 21. Наиболее вероятная скорость находится из выражения 1) 22. Средняя скорость молекул газа находится из выражения 1)
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.169 (0.01 с.) |

 ; 2)
; 2) 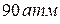 ; 3)
; 3)  .
.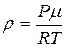 ; 2)
; 2) 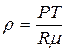 ; 3)
; 3) 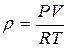 ,
,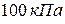 и температуре
и температуре 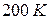 равна
равна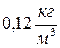 ; 2)
; 2) 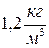 ; 3)
; 3)  .
.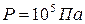 ,
, 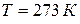 ).
).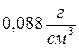 ; 2)
; 2) 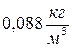 ; 3)
; 3) 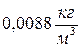 .
. и температуре
и температуре  (молярная масса кислорода
(молярная масса кислорода 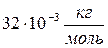 ).
).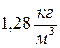 ; 2)
; 2) 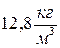 ; 3)
; 3) 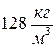 .
. равна
равна  . Найти молярную массу газа.
. Найти молярную массу газа.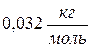 ; 2)
; 2) 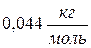 ; 3)
; 3) 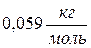 .
. ; 2)
; 2)  ; 3)
; 3)  .
.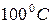 . До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 2 раза?
. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 2 раза? ; 2)
; 2) 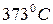 ; 3)
; 3) 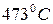 .
. ; 2)
; 2)  ; 3)
; 3) 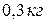 .
. .
. ; 2)
; 2) 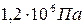 ; 3)
; 3) 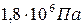 .
.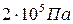 при температуре 400 К. Определить давление после того, как половину массы газа выпустили из сосуда, а температура понизилась на 50 К.
при температуре 400 К. Определить давление после того, как половину массы газа выпустили из сосуда, а температура понизилась на 50 К. ; 2)
; 2) 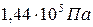 ; 3)
; 3) 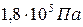 .
. он имеет плотность
он имеет плотность 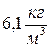 .
.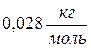 ; 2)
; 2) 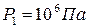 и температура
и температура  , а в другом
, а в другом  и
и 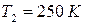 . Сосуды соединили и охладили до 300 К. Определить установившееся давление.
. Сосуды соединили и охладили до 300 К. Определить установившееся давление.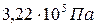 ; 2)
; 2) 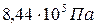 ; 3)
; 3) 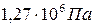 .
.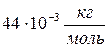 ). Баллон рассчитан на давления до
). Баллон рассчитан на давления до 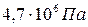 . До какой температуры можно нагревать газ в баллоне?
. До какой температуры можно нагревать газ в баллоне? . Графики перерисованы в координатах
. Графики перерисованы в координатах  Какой из них является верным?
Какой из них является верным? 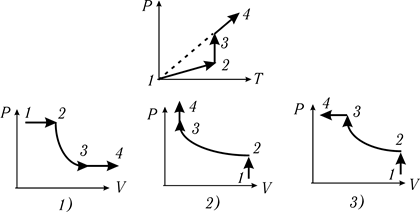
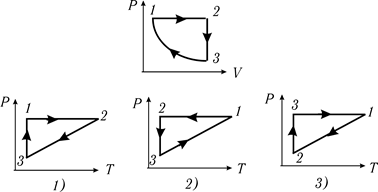
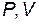 . Какой рисунок верен?
. Какой рисунок верен?
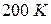 ).
).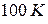 ;
; до
до 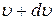 ;
; до
до  ;
; ; 2)
; 2) 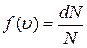 ; 3)
; 3) 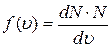 .
. ;
;


 На рисунке показаны кривые распределения Максвелла при двух температурах. Как соотносятся температуры?
На рисунке показаны кривые распределения Максвелла при двух температурах. Как соотносятся температуры? ;
;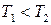 ;
;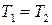 .
. определяет
определяет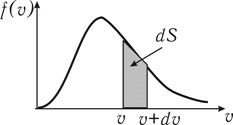
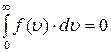 ; 2)
; 2)  ; 3)
; 3) 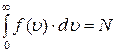 .
.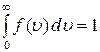 ; 2)
; 2) 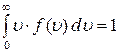 ; 3)
; 3)  .
.


