
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ньютоновские и неньютоновские жидкости .Ламинарное и турбулентное течение жидкости. Число РейнольдсаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ньютоновские и неньютоновские жидкости.
Жидкости, не подчиняющиеся уравнению относят к неньютоновским. Для них вязкость h зависит от скорости течения (градиента скорости dv/dx) жидкости. Такие жидкости содержат молекулы или частицы, склонные к образованию пространственных структур. Их вязкость при прочих равных условиях много больше, чем у ньютоновских жидкостей. Увеличение вязкости происходит потому, что при течении этих жидкостей работа внешней силы затрачивается не только на преодоление истинной, ньютоновской, вязкости, но и на разрушение структуры связанных элементов. Примерами неньютоновских жидкостей являются суспензии, эмульсии, растворы макромолекул (например, некоторых белков), цельная кровь. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских – аномальной. Ламинарное и турбулентное движение жидкости. Ламинарным называется движение жидкости при малых скоростях, когда отдельные элементарные струйки движутся параллельно оси потока. Это движение следует рассматривать как движение отдельных слоев, происходящее без перемешивания частиц. Турбулентное движение - движение, которое при увеличении скорости становится неупорядоченным, частицы жидкости меняют величину и направление скорости, образуя вихри. Число Рейнольдса. Определяет режим движения жидкости.
v-скорость потока d-диаметр трубки ню-кинематический коэффициент вязкости Если 14.Основные положения молекулярно-кинетической теории (мкт). Опыты подтверждающие мкт. Основное уравнение мкт. Молекулярно- кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ. В основе молекулярно-кинетической теории лежат три основных положения:
Подтверждение: Основное уравнение мкт
15.Поверхностный слой в жидкостях. Коэф. поверхностного натяжения. Свободная энергия поверхностного слоя жидкости. Свойства вещества в этой межфазовой поверхности, толщиной в несколько поперечников атомов или молекул, отличаются от свойств внутри объёма фазы. Внутри объёма чистого вещества в твёрдом, жидком или газообразном состоянии любая молекула окружена себе подобными молекулами. В пограничном слое молекулы находятся во взаимодействии или с другим числом молекул (другим в сравнении с взаимодействием внутри объёма вещества). Это происходит, например, на границе жидкости с их паром. Среднее значение равнодействующей молекулярных сил притяжения, приложенных к молекуле, которая находится внутри жидкости, близко к нулю.
Свободная энергия поверх.слоя.жид. Эту дополнительную потенциальную энергию молекул поверхностного слоя жидкости называют свободной энергией. За счёт неё может быть произведена работа, связанная с уменьшением свободной поверхности жидкости. И, наоборот, для того, чтобы вывести молекулы, находящиеся внутри жидкости, на её поверхность, нужно преодолеть противодействие молекулярных сил, т.е. произвести работу, которая нужна для увеличения свободной энергии поверхностного слоя жидкости. При этом, изменение свободной энергии прямо пропорционально изменению площади поверхности жидкости. Так как всякая система самопроизвольно переходит в состояние, при котором её потенциальная энергия минимальна, то жидкость должна самопроизвольно переходить в такое состояние, при котором площадь её свободной поверхности имеет наименьшую величину. Например, капля дождя или тумана в воздухе приобретают форму шара, форму, соответствующую наименьшему уровню свободной энергии. Коэффициент поверхностного натяжения – это величина, характеризующая зависимость работы молекулярных сил, идущих на изменение площади свободной поверхности жидкости и самой площади изменения этой поверхности. σ = А/ΔS σ - коэффициент поверхностного натяжения А – работа молекулярных сил по изменению площади поверхности жидкости ΔS - изменение площади поверхности жидкости σ измеряется работой молекулярных сил при уменьшении площади свободной поверхности жидкости на единицу. Коэффициент поверхностного натяжения зависит от рода жидкости и внешних условий, например, температуры
16.Доп.давление под искривленной поверхностью жидкости. Формула Лапласа.
17.Смачивание и несмачивание капилярные явл.Формула Борелли-Жюрена формула Борелли-Жюрена получена в 1670 г. Величина 2а/pg,входящая в правую часть формулы,назыв.капиллярной постоянной;она явл.важной физико-хим.хар-ой жидкости. 18.Первое начало термодинамики.Изопроцессы.Работа идеал.газа при изопроцессах. Общий закон сохран.энергии с учетом процесса теплообмена и внутр.энергии имеет вид V=const A=O Q=▲U При изобарных процессах:
19.Адиабатный процесс. Уравнение Пуассона. Моляр.телоемкости при постоянных давлении и объеме. Уравнение Майера. p∙v*γ=const Графическое изображение адибатного процесса на диаграмме состояний называется адиабатой.
Сравнение между собой Ср и СV приводит к уравнению Майера:
Это уравнение показывает, что Ср больше, чем СV на величину универсальной газовой постоянной R. Это объясняется тем, что при изобарном нагревании газа, в отличие от изохорного нагревания, требуется дополнительное количество теплоты на совершение работы расширения газа. Таким образом, молярная теплоемкость газа определяется лишь числом степеней свободы и не зависит от температуры. Это утверждение справедливо в довольно широком интервале температур лишь для одноатомных газов.Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависит от температуры. 20.Электрические заряды. Закон Кулона. Электрическое поле.Напряженность электрического поля. Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году. Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами. Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона: Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними
Электрическое поле – вид материи с помощью которого взаимодействует электрические заряженные тела Напряженность — векторная величина. С другой стороны, сила, действующая на заряд q со стороны электрического поля, равна
21.Работа по перемещению электрического заряда в электростатическом поле. Потенциал.Эквипотенциальные поверхности Работа сил эл.пол не завсис. От траектории по которой перемещ.заряд в этом поле Поля облад.такими св-ми назыв. потенциальными. величина работы зависит от заряда его нач. и конеч. Положения и значения вектора Е на этом основании вводят понятие разности потенциала ввиде эл.напряжения 22.Постоянный электрический ток. Сила тока.Электрическое сопротивление. Закон Ома для участка цепи
Электрический ток — это упорядоченное движение заряженных частиц в проводнике. Чтобы он возник, следует предварительно создать электрическое поле, под действием которого вышеупомянутые заряженные частицы придут в движение. Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.
где I - сила тока, q - величина заряда (количество электричества), t - время прохождения заряда. Единица силы тока 1 Ампер - сила тока, когда через поперечное сечение проводника в 1 секунду проходит заряд в 1 Кулон. Закон Ома для однородного участка цепи. Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.
где U - напряжение на участке, R - сопротивление участка. 23.Удельное сопротивление. Зависимость сопротивления металлов от температуры. Закон Ома для участка цепи Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока. Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества. Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения. Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Закон Ома для однородного участка цепи. Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.
где U - напряжение на участке, R - сопротивление участка. У большинства металлов удельное сопротивление связанно с температурой линейной зависимости p=po(1+ƪt) ƪ-0.004 Q=A=YUT=Y²Rt= 24.Работа и мощность постоян.тока. Закон Джоуля-Ленца Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника; Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:
По закону сохранения энергии: работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия равна работе тока. В системе СИ:
- отношение работы тока за время t к этому интервалу времени.
В системе СИ:
При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам. Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
где I - сила тока в цепи, R - сопротивление, t - время По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время. В системе СИ: [Q] = 1 Дж. 25.Магнитное поле. Индукция магнитного поля. Сила Лоренца Магнитное поле -особый вид материи, по средствам которого взаимодействуют движ.электрич.заряды. Магнитное поле удобно изображать с помощью силовых линий В системе СИ магнитная индукция - силовая характеристика магнитного поля, сходно тому, как напряженность электрического поля выражает силовую характеристику электрического поля. Зная индукцию магнитного поля, можно просчитать его силу, воздействующую на проводник с током, по формуле: F = BI l. В проводнике с током заряды движутся не только хаотически в разных направлениях, но также в определенном направлении. На каждый из зарядов воздействует магнитная сила, которая передается проводнику. Сумма всех сил от хаотического движения равна нулю, а сумма сил направленного движения называется силой Ампера. В общем случае величина силы, которая воздействует на проводник с током, размещенный в магнитное поле, определяется законом Ампера: F = BI l sin α, где α – угол между направленностью тока (I) и вектором магнитного поля (В). Индукция магнитного поля численно равняется силе, с которой воздействует магнитное поле на единичный элемент тока, перпендикулярно расположенный к вектору индукции. Магнитная индукция зависит от свойств среды. Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца. Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
Сила Ампера равна
где Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону). Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы. 26.Закон Ампера. Правило левой руки.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.01 с.) |


 – ламинарный, если
– ламинарный, если  – турбулентный режим.
– турбулентный режим. - основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи:
- основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи: 

 пласа
пласа



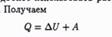 Q-все кол-во теплоты передав.сист.расходуется на совершение работы(а) и изменение внутр.сист энергии▲U.
Q-все кол-во теплоты передав.сист.расходуется на совершение работы(а) и изменение внутр.сист энергии▲U. =
= 
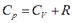 .
.
 ≈ 8,854187817·10−12 Ф/м — электрическая постоянная.
≈ 8,854187817·10−12 Ф/м — электрическая постоянная. , действующей на помещенный в данную точку поля заряд, к этому заряду
, действующей на помещенный в данную точку поля заряд, к этому заряду  для каждой точки поля не зависит от заряда и может рассматриваться как силовая характеристика поля — напряженность электрического поля:
для каждой точки поля не зависит от заряда и может рассматриваться как силовая характеристика поля — напряженность электрического поля:  .
.





 (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется
(при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется 

 t
t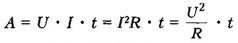


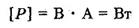
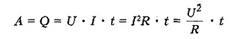

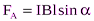 , сила тока равна
, сила тока равна 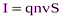 . Подставив эти выражения в формулу для силы Лоренца, получим:
. Подставив эти выражения в формулу для силы Лоренца, получим:
 - угол между векторами скорости и магнитной индукции.
- угол между векторами скорости и магнитной индукции.


