
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия перехода от ламинарного к турбулентному режиму течения неньютоновской жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Известно, что для бингамовской жидкости условия перехода от структурного режима течения по бесконечно длинной цилиндрической трубе круглого сечения к турбулентному определяются как
откуда следует
число Рейнольдса; Не = ρ — плотность критическом режиме течения; α=τо/τa; τa — касательное напряжение на стенке трубы при жидкости; d — диаметр трубы; wср.кр — среднеобъемная скорость жидкости при Здесь Rekp = ρwср. кр d/η — критическое критическом режиме течения. Анализ многочисленных экспериментальных данных показал, что при Не<105 такой метод расчета дает вполне удовлетворительные результаты. Наряду с уравнением Шведова—Бингама для описания реологического поведения некоторых типов нефти используется степенной закон При этом обобщенный критерий Рейнольдcа Re '
Рассмотрим теперь вопрос о том, как найти численное значение величины Reкр по известным бингамовским характеристикам жидкости. Если по данному трубопроводу течет жидкость, то очевидно, что переход от структурного режима ее течения к турбулентному будет происходить при определенных значениях среднеобъемной скорости wср, касательного напряжения τ и градиента скорости на стенке, не зависящих от того, какой именно закон выбран для описания реологического поведения этой жидкости. Следовательно, если известны бингамовские характеристики жидкости τo и η то значения k и п должны быть выбраны так, чтобы при критическом режиме течения значения величины среднеобъемных скоростей получились одинаковыми независимо от вида реологического уравнения. Для жидкости, следующей степенному закону, величина среднеобъемной скорости при критическом режиме течения может быть найдена как wкр=
Второе уравнение может быть получено из условия равенства касательных напряжений и градиентов скорости на стенке трубы при критическом режиме течения тa = τ0 +
Совместное решение этих уравнений дает
Внеся последнее значение в выражение для Re ', получим
Связь между величинами α и Senкр, полученная из точного решения уравнения Букингама, имеет вид
где
Таким образом, с помощью выражения (27), (28) и (29) может быть установлена однозначная связь между величинами
Результаты расчетов по формулам (27), (28), (29) и (30) приведены на рис. Непосредственно из рисунка видно, что значениям Не <105 соответствуют значения n>0,4. При этом величина В заключение следует отметить, что найденные по формулам (28) значения k и п справедливы лишь для критического режима течения. Если перепад давления р<ркр (ркр —перепад давления при критическом режиме течения), то средне-объемные скорости, найденные из уравнения Бингама — Шведова и степенного закона, будут различаться между собой тем больше, чем больше величина р отличается от ркр. Все известные нефти нашей страны можно отнести к одной из следующих групп: Вязкие жидкости (ньютоновские и псевдопластичные) и вязко-пластичные (линейно вязко-пластичные или бингамовские и нелинейно вязко-пластичные). Для описания кривых течения таких жидкостей существует более двадцати реологических моделей. Реологические исследования нефтепродуктов показывают, что в рабочем диапазоне градиентов скоростей промышленных трубопроводов, наиболее общей моделью, описывающей обе группы жидкостей является модель Балкли - Гершеля:
где τ – напряжение сдвига; τ0 – предельное напряжение сдвига; k – мера консистенции жидкости; – показатель поведения жидкости; S- градиент скорости. При τ0=0 (31) описывает псевдопластичную жидкость. При n=1 уравнение (31) переходит в уравнение бингамовской жидкости. При τ0=0 и n=1 уравнение (31) описывает течения ньютоновской жидкости. После проведения реологических исследований и построения кривых τ – S для различных температур можно определить какому виду отнести исследуемую нефть и рассчитать параметры τ0 k n. Для расчета трубопровода при турбулентном режиме течения, когда нефть проявляет вязко-пластичные свойства, общепринятой методики расчета нет. При изотермическом течении в каждом конкретном случае применяются полученные на основе экспериментов и теории подобия формулы вида
Располагая реологическими характеристиками, можно выполнить гидравлический расчет трубопровода по следующей методике. Для определения режима течения нефти в изотермическом трубопроводе рассчитывается параметр Хедстрема (He) и обобщенный параметр Рейнольдса (Re*)
где ЛЕКЦИЯ № 9 Предварительно рассмотрим задачу о течении жидкости плотности Задан требуемый расход Q, надо рассчитать необходимый для его получения перепад давления на заданном участке трубы длиной l. Отвлекаясь от объемных сил (в данном случае силы тяжести) и принимая во внимание стационарность задачи получим, что среди чисел подобия останутся лишь число Эйлера
Определим, как это было сделано ранее, коэффициент сопротивления λ трубы круглого сечения формулой, согласно формуле сопротивления (Eu=λ/2)
при этом будем иметь λ=f(Re). Согласно закону Пуазейля: при установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объемный расход пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса (или диаметра)
Если определить из этого закона
и подставить в формулу сопротивления, то после простых приведенийполучим следующий закон сопротивления для цилиндрических круглых труб:
Формула сопротивления (*) только внешне имеет вид квадратичной зависимости от средней скорости. Истинная зависимость от скорости определяется лишь на основании закона сопротивления, выводимого из уравнения движения жидкости. Для приближенной оценки сопротивления цилиндрических труб сложного фигурного профиля применяют прием сравнения сопротивлений этих труб с сопротивлением «эквивалентной» им по сопротивлению трубы круглого сечения, у которой за радиус (или диаметр) принимается так называемый «гидравлический» радиус rг (или диаметр dг= 2rг), равный отношению площади нормального сечения S трубы к периметру P сечения:
Прием этот достаточно груб и имеет смысл только, если у сравниваемых труб сечения геометрически близки друг к другу. Для выяснения смысла этого приема, рассмотрим связь между перепадом давления
где через
т.е. среднее по периметру цилиндрической трубы напряжение трения равно перепаду давления на участке трубы длиной в гидравлический радиус. В частном случае круглой трубы:
Напряжение трения в круглой трубе совпадает по величине с перепадом давления на участке длиной в половину радиуса трубы, т. е.
Проведем в плоскости нормального сечения трубы замкнутый контур С, подобный относительно некоторого центра подобия О контуру Сw, ограничивающему сечение. Применяя формулу (**) к сечениям С и Сw и сохраняя значок w для величин, относящихся к внешнему контуру найдем
откуда следует, что средние значения напряжений трения по подобным контурам относятся как гидравлические радиусы труб, имеющих эти контуры сечений
В случае трубы круглого сечения ( Будет выполняться равенство
выражающее линейность связи между напряжением трения, приложенным к площадке, перпендикулярной к радиус-вектору любой точки некоторого сечения, и величиной этого радиус-вектора. Равенство (***) в дальнейшем будет применяться неоднократно. Отметим, что при выводе (**) никак не использовалась ламинарность движения и свойственная этому режиму эпюра скоростей Таким образом, соотношение (**) может быть применено и к турбулентному движению жидкости по цилиндрической трубе произвольной формы сечения Соотношения (*), (**), (***), (****) выражающие баланс движущего жидксть перепада давления с тормозящим движение сопротивлением трения, может применяться к движениям любых сплошных сред по цилиндрическим трубам, в частности к движениям неньютоновских жидкостей, каковыми являются нефтяные дисперсные системы. Ранее для неньютоновской вязкой жидкости было введено понятие кажущейся вязкости:
и текучести
В отличие от ньютоновской жидкости величины При движении неньютоновской вязкой жидкости по трубе радиусом
где
Распределение скорости по сечению трубы определяется по формуле
где При любом виде функции
Среднеобъемная скорость, представляющая собой отношение расхода жидкости к площади сечения потока, вычисляется следующим образом:
Установлено, что перепад давления потерянный на сопротивление, всегда растет с увеличением среднеобъемной скорости. Формулы (2), (3) справедливы при отсутствии пристенного скольжения. При вращательном движении неньютоновской вязкой жидкости между двумя соосными цилиндрами распределение касательного напряжения по радиусу имеет вид:
где M — момент сил трения, действующих на единицу длины цилиндра. Угловая скорость наружного цилиндра Ω при отсутствии пристенного скольжения и неподвижном внутреннем цилиндре определяется по формуле
где
|
||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.234.200 (0.008 с.) |


 (27)
(27) критерий Хедстрема;
критерий Хедстрема; (k — мера консистенции; n — показатель поведения жидкости).
(k — мера консистенции; n — показатель поведения жидкости). имеет вид:
имеет вид: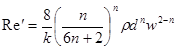
 . Для бингамовской жидкости величина wкр может быть записана в виде
. Для бингамовской жидкости величина wкр может быть записана в виде  критерий Сен-Венана; Senкр—значение критерия Сен-Венана при критическом режиме течения. Следовательно, при критическом режиме течения имеет место равенство
критерий Сен-Венана; Senкр—значение критерия Сен-Венана при критическом режиме течения. Следовательно, при критическом режиме течения имеет место равенство
 =
=  , откуда следует
, откуда следует
 (28)
(28) (29)
(29) (30)
(30)
 , α и Reкр.
, α и Reкр.
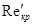 меняется незначительно и в практических расчетах может приниматься равной
меняется незначительно и в практических расчетах может приниматься равной  (31)
(31)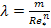
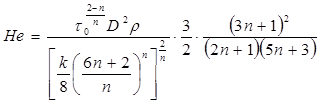
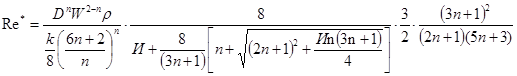
 параметр Ильюшина; D –диаметр трубопровода; W –скорость жидкости в трубопроводе; ρ – плотность жидкости
параметр Ильюшина; D –диаметр трубопровода; W –скорость жидкости в трубопроводе; ρ – плотность жидкости и с коэффициентом динамической вязкости
и с коэффициентом динамической вязкости  сквозь горизонтальную цилиндрическую трубку радиусa
сквозь горизонтальную цилиндрическую трубку радиусa  под действием постоянного перепада давлений
под действием постоянного перепада давлений  на участке трубы длиной l. При этом через трубку проходит также постоянный секундный объемный расход Q. Из двух возможных рассмотрим следующую постановку задачи. Применим метод подобия, основанный на анализе размерностей входящих в рассматриваемую задачу величин:
на участке трубы длиной l. При этом через трубку проходит также постоянный секундный объемный расход Q. Из двух возможных рассмотрим следующую постановку задачи. Применим метод подобия, основанный на анализе размерностей входящих в рассматриваемую задачу величин: и число Рейнольдса
и число Рейнольдса  . В этом случае (подлежит определению
. В этом случае (подлежит определению  ) критерием подобия будет число Рейнольдса Re, а число Эйлера явится его функцией.
) критерием подобия будет число Рейнольдса Re, а число Эйлера явится его функцией. (*)
(*)
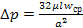
 .
.
 на некотором, произвольно выбранном участке трубы l и суммарным трением по внутренней, так называемой «смоченной» поверхности этой трубы. Примем во внимание, что движение стационарно (одинаково во всех сечениях). Это соответствует равновесию объема жидкости, ограниченного двумя сечениями S1=S2=S трубы, находящимися друг от друга на расстоянии l, и боковой поверхностью трубы, равной произведению периметра сечения Р на длину участка l. Условием равновесия служит очевидное равенство (
на некотором, произвольно выбранном участке трубы l и суммарным трением по внутренней, так называемой «смоченной» поверхности этой трубы. Примем во внимание, что движение стационарно (одинаково во всех сечениях). Это соответствует равновесию объема жидкости, ограниченного двумя сечениями S1=S2=S трубы, находящимися друг от друга на расстоянии l, и боковой поверхностью трубы, равной произведению периметра сечения Р на длину участка l. Условием равновесия служит очевидное равенство ( - переменное, в общем случае, по периметру сечения напряжение трения, ds –дифференциал дуги периметра)
- переменное, в общем случае, по периметру сечения напряжение трения, ds –дифференциал дуги периметра) ,
, обозначено среднее по периметру напряжение трения
обозначено среднее по периметру напряжение трения  (**)
(**)
 (***)
(***)

 )
) , (****)
, (****) (1)
(1) (2)
(2)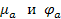 — не константы, а функции касательного напряжения.
— не константы, а функции касательного напряжения. под действием перепада давления
под действием перепада давления  распределение касательного напряжения по радиусу, как и в случае ньютоновской жидкости, имеет вид:
распределение касательного напряжения по радиусу, как и в случае ньютоновской жидкости, имеет вид: (3)
(3)
 касательное напряжение на стенке трубы, определяемое из соотношения:
касательное напряжение на стенке трубы, определяемое из соотношения: (4)
(4)
 задается реологическим уравнением жидкости
задается реологическим уравнением жидкости  .
.
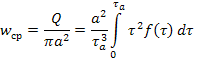
 (7)
(7)
 — напряжения сил трения на поверхностях внутреннего и наружного цилиндров соответственно.
— напряжения сил трения на поверхностях внутреннего и наружного цилиндров соответственно.


