Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание нестационарных процессов в неньютоновских средахСодержание книги
Поиск на нашем сайте Согласно представлениям структурно-кинетической теории [1-5] процессы разрушения и восстановления структуры в неньютоновских средах можно схематично представить как прямую и обратную химические реакции. Пусть N0 - число структурных связей в единице объема материала до начала разрушения структуры, N(t) и N1 (t) - число разрушенных и неразрушенных связей соответственно, s(t) =N(t)/N0(t) s1 (t) =1- s (t) – доли (или концентрации) этих связей. Ясно, что чем больше концентрация неразрушенных связей, тем больше связей может распасться в единицу времени. В то же время увеличение концентрации разрушенных связей приводит к возрастанию интенсивности их восстановления (поскольку увеличивается вероятность встречи разорванных «концов» пространственной сетки). Поэтому по мере тиксотропного разрушения структуры при Последовательное развитие этих представлений с использованием подходов, разработанных в теории химических реакций, приводит к кинетическим уравнениям вида
моделирующим нестационарные процессы в неньютоновских средах. Эффективная вязкость материалов Простейшее линейное уравнение вида (1) можно записать по аналогии с кинетическим уравнением первого порядка:
где k1 = k1 (
Согласно (3) при s = 0 (неразрушенная структура) Из (2) и (3) легко получить уравнение
где Решение (4) с начальным условием
Согласно этому соотношению, Обобщением (2) является нелинейное кинетическое уравнение, предложенное Денни и Бродки (D. A. Denny, R. S. Brodkey, 1962 г.) [Виноградов Г.В., Малкин А.Я. Реология полимеров. – М.: Химия, 1977. -439 с.]:
где n и т - постоянные, аналогичные стехиометрическим коэффициентам, используемым в химической кинетике. В теории Денни и Бродки принимается, что
Предполагается также, что эффективная вязкость определяется соотношением (3). При достаточно продолжительном деформировании с постоянной скоростью сдвига условием
Соотношение в неявном виде определяет равновесную зависимость кажущейся вязкости от скорости сдвига Рассмотрим некоторые возможные пути уточнения кинетических моделей неньютоновских сред. Как известно, скорость диссипации механической энергии в единице объема жидкости равна W = k1=k1 Повреждения пространственной «сетки» могут служить центрами, в окрестностях которых процессы деструкции резко ускоряются («где тонко, там и рвется»), поэтому константу скорости разрушения структуры можно считать возрастающей функцией концентрации разрушенных связей s. Приведенные выше соображения можно учесть, например, в следующем кинетическом уравнении:
где kо - некоторая постоянная. Эффективная вязкость сильнее всего меняется также на начальной стадии разрушения структуры, поэтому линейная связь (3) качественно неверна. Вместо нее целесообразно использовать экспоненциальные зависимости вида
Здесь величина s0 определяет область, в которой эффективная вязкость меняется наиболее значительно (рис. 3.1).
Рис. 3.1. Зависимость эффективной вязкости от концентрации разрушенных связей Для описания нестационарных процессов в средах характеризующихся образованием структурных связей под действием деформаций (реопектических) может быть предложено кинетическое уравнение
где q - концентрация структурных связей, образовавшихся в результате сдвиговых деформаций, k1 и k2 - константы скоростей разрушения и восстановления связей, m - порядок «реакции» разрушения структуры. Согласно (9) при малых Считая, что состояние неньютоновской среды можно характеризовать всего лишь одной переменной - концентрацией связей - мы тем самым неявно считаем все структурные связи одинаковыми. Это, конечно, не так, поскольку реологически сложные среды состоят из структурных единиц различного масштаба (молекул, их ассоциатов, макромолекул, кластеров, ассоциатов кластеров и т. д.), образующих некоторую иерархически построенную систему. Реологическое поведение структурных единиц и теснота связи между ними на каждом уровне этой иерархии различны. Поэтому эффективную вязкость среды следует считать функцией многих переменных
При построении таких моделей делаются более или менее правдоподобные рассуждения об основных структурных единицах и схеме «реакций» с их участием. Однако практическая ценность подобных теорий весьма мала, поскольку «внутренние» переменные si,- являются ненаблюдаемыми - в настоящее время еще не разработаны методы экспериментального определения этих величин. Нужно иметь в виду так называемый принцип неопределенности, который формулируется примерно так: с увеличением сложности системы возможность точного, имеющего практическое значение, представления уменьшается. Одно из следствий этого принципа заключается в том, что неопределенность решения увеличивается при более глубоком анализе реальной задачи Отметим, что в случае одной переменной s модель (1) может быть, в принципе, переписана относительно наблюдаемой величины Система (10) содержит большое число теоретически не определяемых параметров, подбором которых можно объяснить любые экспериментальные данные, поэтому проверка ее адекватности невозможна. Более того, одним и тем же экспериментальным данным могут удовлетворять различные наборы параметров. Все это лишает модели вида (10) предсказательной силы. Здесь уместен анекдот, прекрасно описывающий ситуацию с теориями, в которых параметры «подгоняют» под экспериментальные результаты. Офицер северян во время гражданской войны в США видит на дверях амбаров множество от руки нарисованных мишеней, в середине каждой из которых - след пули, попавшей точно в «яблочко». «Кто это тут упражнялся? Неплохой стрелок», - говорит он. «Да это Билли Джонс баловался с кольтом. Но если честно, то он совсем не умеет стрелять». «Как же так?» «Так он сначала стреляет, а уже потом рисует круги вокруг пробоины». Иными словами, сложность модели (10) не соответствует объему доступной на данное время теоретической и экспериментальной информации. Приемлемым выходом в этой ситуации может стать использование дифференциально-разностных моделей (т. е. дифференциальных уравнений с запаздывающим аргументом) вида
Возможность замены системы (10) одним уравнением (11) физически можно объяснить тем, что цепочка «реакций» разрушения крупных структурных единиц на более мелкие (или восстановления крупных структурных единиц из мелких) приводит к некоторому запаздыванию в процессах структурообразования. Наличие отклоняющегося аргумента в модели (11) позволяет в какой-то мере учесть это запаздывание, не выписывая в явном виде кинетические уравнения для всех иерархических уровней. Для примера рассмотрим систему
Исключив переменную у, получим дифференциальное уравнение второго порядка x'' + x = 0, имеющее частное решение х = С • sin t. Легко проверить, что эта функция является одновременно и решением уравнения
Таким образом, дифференциально-разностное уравнение первого порядка с отклоняющимся аргументом в каком-то смысле аппроксимирует систему дифференциальных уравнений. Релаксационные явления в реофизически сложных средах связаны с медленным развитием процессов перегруппировки структурных единиц различного масштаба. (Так, в случае полимеров таковыми являются гибкие молекулы, их отдельные сегменты или же пачки, образованные этими молекулами.) Эти процессы приводят к запаздыванию изменений деформации от изменения напряжения (гистерезис, упругое последействие, релаксация напряжения и т. д.) и могут быть описаны с помощью моделей упругих тел с внутренним трением и вязких тел, обладающих упругостью. Механические модели вязкоупругих тел полезны для понимания качественных особенностей явлений релаксации, но их применение к количественному описанию реальных материалов требует построения очень сложных систем, состоящих из большого числа различных пружин и вязких элементов (что связано с наличием иерархии структурных единиц различного масштаба, приводящей к иерархии широко распределенных времен релаксации). Ясно, что сложные модели не могут оказаться эффективными - слишком велики трудности, связанные с определением многочисленных релаксационных параметров по экспериментальным данным, а также с решением задач моделирования движения сред с широким спектром времен релаксации. Андрианов И.В., МаневичЛ.И. Асимптология: идеи, методы, результаты. –М.: АЛАН,1994. – 159 с.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 =const скорость разрушения связей уменьшается, а скорость восстановления связей растет. В конце концов, скорости образования и разрушения структуры станут равными друг другу и наступит динамическое равновесие, характеризующееся некоторым стационарным значением
=const скорость разрушения связей уменьшается, а скорость восстановления связей растет. В конце концов, скорости образования и разрушения структуры станут равными друг другу и наступит динамическое равновесие, характеризующееся некоторым стационарным значением  (τ и
(τ и 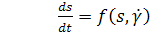 (1)
(1)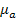 считается некоторой функцией величины s, требующей специального задания:
считается некоторой функцией величины s, требующей специального задания: 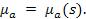
 (2)
(2) а =
а = 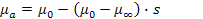 (3)
(3)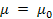 , а при s = 1 (полностью разрушенная структура)
, а при s = 1 (полностью разрушенная структура) 
 (4)
(4)
 ) вид:
) вид:
 . Следовательно, функция
. Следовательно, функция  (
(
 , то величина
, то величина  (5)
(5)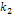 = const, а константа скорости разрушения является возрастающей функцией скорости сдвига:
= const, а константа скорости разрушения является возрастающей функцией скорости сдвига: 1=k0
1=k0  .
.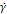 устанавливается равновесное состояние, определяемое
устанавливается равновесное состояние, определяемое = 0, которое можно, используя (3) и (5), переписать в виде:
= 0, которое можно, используя (3) и (5), переписать в виде: (6)
(6) a =
a = 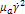 Естественно предположить, что часть этой энергии тратится на разрушение структурных связей, поэтому константу скорости разрушения k1 можно считать функцией величины W. Это позволяет уточнить вид зависимости k1 от скорости сдвига:
Естественно предположить, что часть этой энергии тратится на разрушение структурных связей, поэтому константу скорости разрушения k1 можно считать функцией величины W. Это позволяет уточнить вид зависимости k1 от скорости сдвига:
 (7)
(7)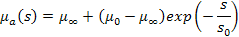

 (9)
(9) a =
a =  (10)
(10)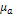 (см., например, уравнение 4).
(см., например, уравнение 4). (11)
(11)