
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон распределения скорости в сечении круглой цилиндрической трубы при прямолинейном движении вязко-пластичной жидкостиСодержание книги
Поиск на нашем сайте
Для вязко-пластичной жидкости в соответствии с ранее приведенными зависимостями:
Распределение скорости получим, воспользовавшись формулой (5) и учитывая, что определяется по (9)
При
При
Учитывая результаты интегрирования, распределение скорости записывается следующим образом:
Обозначим радиус, при котором касательное напряжение становится равным
где Учитывая, что
После несложных преобразований, получим:
Следовательно, эпюра скоростей имеет вид, показанный на рис. 2 и состоит частью из поверхности параболоида вращения (от стенки трубы до цилиндрической поверхности радиуса В некоторых случаях такой «твердый стержень» образуется в непосредственной близости к стенке трубы и по свойству «прилипания» вязкой жидкости к твердой поверхности может остаться неподвижным. При этом эффективный диаметр трубы (трубопровода) уменьшается и, как правило, снижается пропускная способность.
Режим движения, при котором имеет место распределение скоростей, показанное на рис. 2, получил название «структурного режима движения». Имея эпюру скоростей, легко определить секундный объемный расход Q вязко-пластичной жидкости сквозь сечение трубы. Расход жидкости через поперечное сечение трубы определится из выражения:
Формула (13) также впервые была получена Букингамом. При
Отметим, что Формула (14) часто используется в литературе по бурению нефтяных и газовых скважин. Точность ее увеличивается с уменьшением
При этом
Для малых значений ξ можно записать приближенное соотношение:
Следовательно, для малых значений ξ расход приближенно равен
Если принять радиус ядра достаточно большим и близким к
Например при ξ=0,2 ( С целью определения реологических параметров вязко-пластичной жидкости Угловая скорость наружного цилиндра определяется по формуле (8). Так как по условию касательное напряжение на стенке
В соответствии с формулой (7)
Подставив эти соотношения в (17), получим:
Пример При проведении опыта на ротационном вискозиметре было измерено, что при Ω=60с-1 M=0,05Н, а при Ω=30с-1 M=0,03Н. Считая, что жидкость вязко-пластичная найти величины и Решение Записывая в общем виде соотношение (18) для двух значений Ω (Ω1,Ω2) и соответствующих двух значений М (М1,М2) получим два линейных уравнения, разрешая которые находим:
Подставляя исходные данные в последние соотношения, получим η= 0,074 Па с; τ0= 2,73 Па Примеры для самостоятельного рассмотрения 1. Вывести формулу для зависимости расхода Q при течении вязко-пластичной нефти в трубе радиусом 2. Найти закон распределения скорости по радиусу при течении нефти, подчиняющейся степенной зависимости движения жидкости в круглой трубе радиусом 3. Вывести формулу зависимости расхода Q при течении «степенной нефти» в трубе радиусом 4. По трубе длиной 5. По трубе течет «степенная нефть». Найти отношение максимальной скорости wmax к средней скорости wср. Ответ: wmax/wср= (3n+1)/(n+1). 6. Определить момент сил трения, действующих на единицу длины внутреннего цилиндра ротационного вискозиметра, если наружный цилиндр вращается с угловой скоростью Ω=10 с-1, τ0= 5 Н/м2, η=1 Па⋅ с, радиус наружного цилиндра Ответ: М=0,026 Н. 7. По трубе длиной 8.Вязко-пластичная нефть обладает начальным напряжением сдвига τ0= 2,5 Па и коэффициентом пластической вязкости η =0,2 Па⋅ с. Определить кажущуюся вязкость и текучесть при скорости сдвига 9.Пользуясь π-теоремой, определить от каких безразмерных параметров зависит коэффициент гидравлического сопротивления при течении вязко-пластичной жидкости в трубе. Известно, что для бингамовской жидкости условия перехода от структурного режима течения по бесконечно длинной цилиндрической трубе круглого сечения к турбулентному определяются как
откуда следует
Здесь Rekp = ρwср. кр d/η — критическое число Рейнольдса; Не = ρ — плотность жидкости; d — диаметр трубы; wср.кр — среднеобъемная скорость жидкости при критическом режиме течения; α=τо/τa; τa — касательное напряжение на стенке трубы при критическом режиме течения. Анализ многочисленных экспериментальных данных показал, что при Не<105 такой метод расчета дает вполне удовлетворительные результаты. Наряду с уравнением Шведова—Бингама для описания реологического поведения некоторых типов нефти используется степенной закон При этом обобщенный критерий Рейнольдcа Re'
Рассмотрим теперь вопрос о том, как найти численное значение величины Reкр по известным бингамовским характеристикам жидкости. Если по данному трубопроводу течет жидкость, то очевидно, что переход от структурного режима ее течения к турбулентному будет происходить при определенных значениях среднеобъемной скорости wср, касательного напряжения τ и-градиента скорости на стенке, не зависящих от того, какой именно закон выбран для описания реологического поведения этой жидкости. Следовательно, если известны бингамовские характеристики жидкости τo и η то значения k и п должны быть выбраны так, чтобы при критическом режиме течения значения величины среднеобъемных скоростей получились одинаковыми независимо от вида реологического уравнения. Для жидкости, следующей степенному закону, величина среднеобъемной скорости при критическом режиме течения может быть найдена как wкр=
Второе уравнение может быть получено из условия равенства касательных напряжений и градиентов скорости на стенке трубы при критическом режиме течения тa = τ0 +
Совместное решение этих уравнений дает
Внеся последнее значение в выражение для Re', получим
Связь между величинами α и Senкр, полученная из точного решения уравнения Букингама, имеет вид
где
Таким образом, с помощью выражения (19), (20) и (21) может быть установлена однозначная связь между величинами
Результаты расчетов по формулам (19), (20), (21) и (22) приведены на рис.. Непосредственно из рисунка видно, что значениям Не <105 соответствуют значения n>0,4. При этом величина В заключение следует отметить, что найденные по формулам (20) значения k и п справедливы лишь для критического режима течения. Если перепад давления р<ркр (ркр —перепад давления при критическом режиме течения), то средне-объемные скорости, найденные из уравнения Бингама — Шведова и степенного закона, будут различаться между собой тем больше, чем больше величина р отличается от ркр. Установим закон сопротивления для течения вязко-пластичной нефтяной дисперсной системы в цилиндрических круглых трубах. Используем ту же формулу сопротивления (*), что и для ньютоновской вязкой жидкости. Средне-объемная (средняя по сечению) скорость wср для вязко-пластичной нефти имеет вид:
К сожалению, равенство (23) относительно
с другой стороны из (23) может определено число Рейнольдса Re= Безразмерное число
можно рассматривать как параметрическое (роль параметра играет величина
откуда следует общий вид закона сопротивления движению вязко-пластичной нефти по трубам круглого сечения
Таким образом, в теории подобия течений вязко-пластичной нефти по круглым цилиндрическим трубам имеют место два критерия подобия: o Число Рейнольдса o Число Сен-Венана (так называемый «параметр пластичности»)
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.012 с.) |

 (9)
(9)






 (10)
(10) , через
, через 
 (11)
(11) —перепад давления,
—перепад давления,  длина трубы.
длина трубы.















 формула (13) переходит в известную формулу Пуазейля. Если принять, что формула распределения скоростей справедлива при
формула (13) переходит в известную формулу Пуазейля. Если принять, что формула распределения скоростей справедлива при  т.е. принять, что уравнения движения вязко-пластичной жидкости описывают всю область движения, то формула для определения расхода примет вид:
т.е. принять, что уравнения движения вязко-пластичной жидкости описывают всю область движения, то формула для определения расхода примет вид:

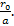 Так, например, при
Так, например, при  третий член в формуле (14) равен
третий член в формуле (14) равен  и им можно пренебречь по сравнению с разностью первых двух членов
и им можно пренебречь по сравнению с разностью первых двух членов  . При этом погрешность в определении Q около -6%. Введем обозначение
. При этом погрешность в определении Q около -6%. Введем обозначение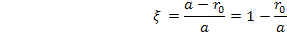


 (15)
(15)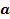 , то приближенно расход можно вычислить по формуле:
, то приближенно расход можно вычислить по формуле:
 =0.8) погрешность при определении Q по формуле (15) составляет около 13%. При значениях ξ <0.2 эта погрешность уменьшается.
=0.8) погрешность при определении Q по формуле (15) составляет около 13%. При значениях ξ <0.2 эта погрешность уменьшается.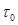 и
и  на ротационном вискозиметре, требуется найти связь между угловой скоростью наружного цилиндра
на ротационном вискозиметре, требуется найти связь между угловой скоростью наружного цилиндра  и моментом сил трения
и моментом сил трения  , действующим на единицу длины цилиндра, считая что напряжение трения на наружном цилиндре
, действующим на единицу длины цилиндра, считая что напряжение трения на наружном цилиндре  .
. , и вся жидкость течет. Подставив (9) в (8), получим:
, и вся жидкость течет. Подставив (9) в (8), получим:
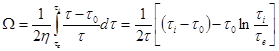 (17)
(17)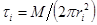

 (18)
(18)
 ;
; 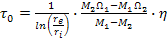
 и длиной
и длиной  от перепада давления
от перепада давления  и реологических параметров нефти
и реологических параметров нефти . Реологические параметры нефти k, n и перепад давления на единицу длины трубы Δp/l считать известными.
. Реологические параметры нефти k, n и перепад давления на единицу длины трубы Δp/l считать известными. и диаметром d=0.1м течет вязко-пластичная нефть с реологическими параметрами η= 0,1 Па с; τ0= 4,5 (Н/м2). Перепад давления Δp=5
и диаметром d=0.1м течет вязко-пластичная нефть с реологическими параметрами η= 0,1 Па с; τ0= 4,5 (Н/м2). Перепад давления Δp=5  105. Найти расход Q и радиус ядра потока r0. Ответ: Q=6,5
105. Найти расход Q и радиус ядра потока r0. Ответ: Q=6,5  ,
, 
 и диаметром d=2 см течет вязко-пластичная нефть. При перепаде давления Δp=104, расход Q=0,01 л/с, а при Δp=3⋅104, расход Q=0,05 л/с. Определить τ0 и η. Ответ: τ0= 1,82 Па; η =0,2 Па⋅ с.
и диаметром d=2 см течет вязко-пластичная нефть. При перепаде давления Δp=104, расход Q=0,01 л/с, а при Δp=3⋅104, расход Q=0,05 л/с. Определить τ0 и η. Ответ: τ0= 1,82 Па; η =0,2 Па⋅ с. =100с-1. Ответ:
=100с-1. Ответ:  =0.125 Па⋅ с
=0.125 Па⋅ с  ;
;
 (19)
(19) критерий Хедстрема;
критерий Хедстрема; (k — мера консистенции; n — показатель поведения жидкости).
(k — мера консистенции; n — показатель поведения жидкости). имеет вид:
имеет вид: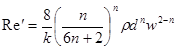
 . Для бингамовской жидкости величина wкр может быть записана в виде
. Для бингамовской жидкости величина wкр может быть записана в виде  критерий Сен-Венана; Sen кр —значение критерия Сен-Венана при критическом режиме течения. Следовательно, при критическом режиме течения имеет место равенство
критерий Сен-Венана; Sen кр —значение критерия Сен-Венана при критическом режиме течения. Следовательно, при критическом режиме течения имеет место равенство
 =
=  , откуда следует
, откуда следует
 (20)
(20) (21)
(21) (22)
(22)
 , α и Reкр.
, α и Reкр.
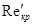 меняется незначительно и в практических расчетах может приниматься равной
меняется незначительно и в практических расчетах может приниматься равной 
 (23)
(23)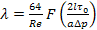 ;
;  (24)
(24)
 (25)
(25)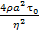 не содержит
не содержит 
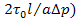 выражение закона сопротивления движению в трубах вязко-пластических жидкостей. Исключая из последней системы равенств параметр
выражение закона сопротивления движению в трубах вязко-пластических жидкостей. Исключая из последней системы равенств параметр  , получим
, получим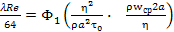
 ,
,  определяющий эффект пластичности нефти. Отметим, что параметр пластичности не влияет на переходной процесс от ламинарного движения к турбулентному.
определяющий эффект пластичности нефти. Отметим, что параметр пластичности не влияет на переходной процесс от ламинарного движения к турбулентному.


