
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние показатели в рядах динамикиСодержание книги
Поиск на нашем сайте При анализе развития явлений часто возникает потребность дать обобщенную характеристику интенсивности развития на длительный период. Для чего используют средние показатели динамики: 1. Средний абсолютный прирост находится по формуле:
где n — число периодов (уровней), включая базисный. 2. Средний темп роста
Когда приходится производить расчет средних темпов роста по периодам различной продолжительности (неравноотстоящие уровни), то используют среднюю геометрическую, взвешенную по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:
где t – интервал времени, в течение которого сохраняется данный темп роста. 3. Средний темп прироста не может быть определен непосредственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо сначала найти средний темп роста, а затем его уменьшить на 100%:
Пример 7.1. Имеются данные о приростах объемов продаж по месяцам (в процентах к предыдущему месяцу): январь – +4,5, февраль – +5,2, март – +2,4, апрель – -2,1. Определить темпы роста и прироста за 4 месяца и среднемесячные значения. Решение: имеем данные о цепных темпах прироста. Преобразуем их в цепные темпы роста по формуле: Тр = Тр + 100%. Получим следующие значения: 104,5; 105,2; 102,4; 97,9 Для расчётов используются только коэффициенты роста: 1,045; 1,052; 1,024; 0,979. Произведение цепных коэффициентов роста дают базисный темп роста. К = 1,045·1,052·1,024·0,979 = 1,1021 Темп роста за 4 месяца Тр = 1,1021·100= 110,21% Темп прироста за 4 месяца Тпр = 110,21 – 100 = +10,21% Средний темп роста находим по формуле средней геометрической простой:
Средний темп роста за 4 месяца Средний темп прироста за 4 месяца 4. Средний уровень интервального ряда находится по формуле средней арифметической простой, если интервалы равны, или по средней арифметической взвешенной, если интервалы не равны:
где t - длительность интервала времени. 5. Средний уровень моментного ряда динамики так исчислить нельзя, так как отдельные уровни содержат элементы повторного счета. а) Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической:
где у1 и уn — значения уровней на начало и конец периода (квартала, года). б) Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:
где t — длительность периода между смежными уровнями. Пример 7.2. Имеются следующие данные об объёмах производства продукции за первый квартал (тыс.шт.) — январь — 67, февраль – 35, март – 59. Определить среднемесячный объем производства за 1 квартал. Решение: по условию задачи имеем интервальный ряд динамики с равными периодами. Среднемесячный объем производства находится по формуле средней арифметической простой:
Пример 7.3. Имеются следующие данные об объёмах производства продукции за первое полугодие (тыс.т.) — среднемесячный объем за 1 квартал — 42, апрель – 35, май – 59, июнь – 61. Определить среднемесячный объем производства за полугодие. Решение: по условию задачи имеем интервальный ряд динамики с неравными периодами. Среднемесячный объем производства находится по формуле средней арифметической взвешенной:
Пример 7.4. Имеются следующие данные об остатках товаров на складе, млн. руб.: 1.01 – 17; на 1.02 – 35; на 1.03 – 59; на 1.04 – 61. Определить среднемесячный остаток сырья и материалов на складе предприятия за I квартал. Решение: По условию задачи имеем моментный ряд динамики с равноотстоящими уровнями, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:
Пример 7.5. Имеются следующие данные об остатках товаров на складе, млн. руб.: 1.01.11 – 17; на 1.05 – 35; на 1.08 – 59; на 1.10 – 61, на 1.01.12 – 22. Определить среднемесячный остаток сырья и материалов на складе предприятия за год. Решение: По условию задачи имеем моментный ряд динамики с неравноотстоящими уровнями, поэтому средний уровень ряда будет исчислен по формуле средней хронологической взвешенной:
Методы анализа основной тенденции (тренда) в рядах динамики Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей тому или иному ряду динамики. Под основной тенденцией развития ряда динамики понимают изменение, определяющее общее направление развития. Это — систематическая составляющая долговременного действия. В некоторых случаях общая тенденция ясно прослеживается в динамике рассматриваемого показателя, в других случаях она может не просматриваться из-за ощутимых случайных колебаний. Например, в отдельные моменты времени сильные колебания розничных цен могут заслонить наличие тенденции к росту или снижению этого показателя. Поэтому для выявления основной тенденции развития в статистике применяются 2 группы методов: а) сглаживание или механическое выравнивание отдельных уровней ряда динамики с использованием фактических значений соседних уровней; б) выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отражала тенденцию, присущую ряду и одновременно освободила его от незначительных колебаний. Распространенным приемом при выявлении тенденции развития является сглаживание ряда динамики. Суть различных приемов сглаживания сводится к замене фактических уровней ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям. Это способствует более четкому проявлению тенденции развития. Метод простой скользящей средней. Алгоритм сглаживания: 1) Определяют длину интервала сглаживания L, включающего в себя L последовательных уровней ряда (не менее трех уровней) 2) Весь период наблюдений разбивают на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1. 3) Рассчитывают средние арифметические из уровней ряда, образующих каждый участок 4) Фактические значения ряда, стоящие в центре каждого участка, заменяют на соответствующие средние значения Пример 7.6. Имеются данные о продажах по месяцам.
Решение. Проведем сглаживание с длиной интервала L=3 уровня. Первый интервал включает в себя первые три уровня. Скользящая средняя будет равна
Это значение относится компании второму месяцу (середина интервала). Аналогично рассчитываются скользящие средние для интервала 2–3–4, 3–4–5, 4–5–6 месяцы.
Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени – y = f(t). При таком подходе изменение явления связывают лишь с течением времени, считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени. Правильно построенная модель должна соответствовать характеру изменения тенденции исследуемого явления. Выбранная функция позволяет получить выровненные или теоретические значения уровней ряда динамики. Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы разной степени, экспоненты, логистические кривые и другие виды.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |


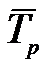 вычисляется по формуле средней геометрической простой из цепных коэффициентов роста:
вычисляется по формуле средней геометрической простой из цепных коэффициентов роста: ,
, 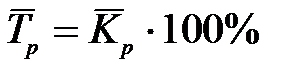 .
.

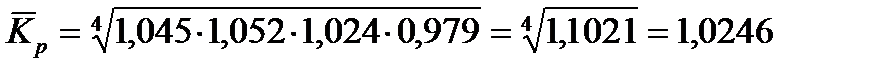
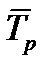 = 1,0246·100= 102,46%
= 1,0246·100= 102,46%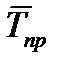 = 102,46 – 100 = +2,46%
= 102,46 – 100 = +2,46% ,
, 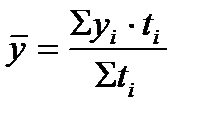 .
.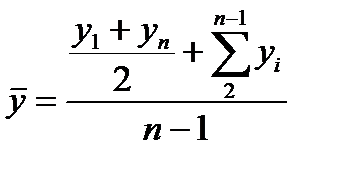 .
.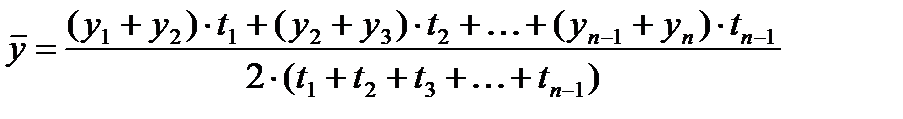 .
. тыс.шт.
тыс.шт.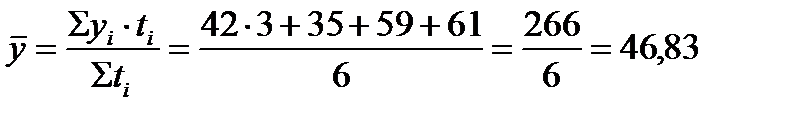 тыс.т.
тыс.т. млн.руб.
млн.руб.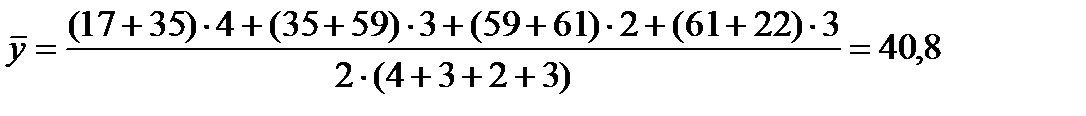 млн.руб.
млн.руб. д.е.
д.е.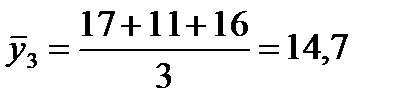 д.е.
д.е. д.е.
д.е. д.е.
д.е.


