
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синхронно-шаговые двигатели. Принцип работы. Возможность применения их для привода вентилятора.Содержание книги
Поиск на нашем сайте
Шаговые двигатели – это электромеханические устройства, преобразующие электрические импульсы напряжения управления в дискретные (скачкообразные) угловые и линейные перемещения ротора с возможной его фиксацией в нужных положениях. Шаговые двигатели (ШД) применяются в качестве исполнительных элементов в системах с дискретным приводом (системах дискретного (импульсного) действия), широко использующихся в схемах автоматики наряду с автоматическими системами непрерывного действия, осуществляемыми с помощью обычных исполнительных двигателей. Частота вращения и суммарный угол поворота вала ШД пропорциональны соответственно частоте и числу поданных импульсов управления. При отсутствии управляющих импульсов ШД находится в режиме фиксированной стоянки и сохраняет конечные результаты предыдущих перемещений. Привод с ШД сочетает возможности глубокого регулирования частоты вращения с возможностью числового задания и надежной фиксации конечных координат. Наибольшее применение ШД получили в электроприводах с программным управлением. ШД делят на 4 основных группы: 1- с постоянными магнитами (активного типа), 2 - реактивные, 3 - индукторные, 4 - линейные Другими особенностями конструктивного исполнения ШД являются: минимальные диаметры роторов; двигатели рассчитываются на большие электромагнитные нагрузки и выполняются с большой степенью точности. Для питания ШД применяются специальные блоки управления, которые обеспечивают преобразование унитарной последовательности импульсов в m-фазную систему напряжений, питающих обмотки ШД через усилители мощности. Обмотки у большинства шаговых двигателей питаются несинусоидальными импульсами напряжения, частота и скважность которых могут изменяться в широких пределах коммутатором, через который осуществляется питание двигателя. Мое мнение! – СШД и вентилятор сочетание несочетаемого. 25. Критерии устойчивости САУ. Области применения. (=8=20) Алгебраические критерии основываются на утверждении, что если все корни характеристического уравнения левые (вещественные части всех корней отрицательны), то все коэффициенты уравнения имеют один знак, т.е. все значения an либо больше нуля, либо меньше нуля одновременно. Это является необходимым условием. АК применяются там, где необходимо просто установить - устойчива САУ или нет, без определения порядка устойчивости. Применяется при составлении алгоритмов программ. Критерий Гурвица. Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все Критерий Рауса. Для устойчивости линейной стационарной системы необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса Частотные критерии устойчивости основаны на связи расположения корней характеристического полинома с годографом этого полинома на комплексной плоскости, т.е. с графиком комплексной функции D(jw) при изменении w от 0 до ∞. По принципу аргумента Коши: контур Критерий Михайлова. Система будет устойчива, если вектор D(jw) при изменении частоты от 0 до +∞ повернется на угол np/2. При этом конец вектора опишет кривую, называемую годографом Михайлова. Годограф начинается на положительной полуоси при D(0) = an, и, при изменении частоты от 0 до ∞, последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, с уходом в бесконечность в n-ом квадранте. Если это правило нарушается, то такая система неустойчива. Критерий Найквиста. Этот критерий основан на связи свойства устойчивости замкнутой системы с формой АФЧХ разомкнутой устойчивой системы. Разомкнутой системой являются все последовательно соединенные блоки от входа системы до точки замыкания обратной связи. Линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если при изменении частоты от 0 до +∞ разность между числом положительных переходов годографа АФЧХ разомкнутой системы через вещественную ось и числом отрицательных переходов равна нулю.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.34 (0.006 с.) |

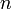 диагональных миноров определителя Гурвица были положительны.
диагональных миноров определителя Гурвица были положительны.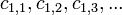 были одного знака. Если это не выполняется, то система неустойчива.
были одного знака. Если это не выполняется, то система неустойчива.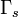 , охватывающий на
, охватывающий на  -плоскости некоторое число неаналитических точек, может быть отображён на другую комплексную плоскость (плоскость
-плоскости некоторое число неаналитических точек, может быть отображён на другую комплексную плоскость (плоскость 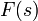 ) при помощи функции
) при помощи функции 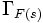 будет охватывать центр
будет охватывать центр  -плоскости
-плоскости  , где
, где 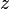 — число нулей, а
— число нулей, а  — число полюсов функции
— число полюсов функции 


