
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторные дифференциальные операции первого порядка. Оператор Гамильтона. Перечислить векторные дифференциальные операции второго порядка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основными дифференциальными операциями (действиями) над скалярным полем Векторные операции – нахождение градиента, дивергенции, ротора, удобно описывать с помощью дифференциального оператора, который обозначается символом
Он приобретает смысл лишь в комбинации со скалярными или векторными функциями. Символическое «умножение» вектора Выразим основные дифференциальные операции с помощью оператора Гамильтона: 1. 2. 3.
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действии с ними надо пользоваться правилами векторной алгебры и правилами дифференцирования. После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применит этот оператор. В результате получаются дифференциальные операции второго порядка. Можно убедиться, что имеется лишь пять дифференциальных операций второго порядка: Дифференциальный оператор
также называется оператором Гамильтона. Запишем основные дифференциальные операции второго порядка, используя оператор Гамильтона: 1. Таким образом, получаем дифференциальное уравнение
которое называется дифференциальным уравнением Лапласа. Это уравнение играет важную роль в различных разделах математической физике. Решениями уравнения Лапласа являются так называемые гармонические функции. 2.
3.
4.
5. 26. Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля. Векторное поле Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела; магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и другие. Приведем некоторые свойства соленоидального поля: 1. В соленоидальном поле 2. Соленоидальное поле является полем ротора некоторого векторного поля, т.е. если Так как 3. В соленоидальном поле
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.01 с.) |

 и векторным полем
и векторным полем  являются: градиент, дивергенция, ротор. Эти действия называются векторными операциями первого порядка (в них участвуют только производные первого порядка).
являются: градиент, дивергенция, ротор. Эти действия называются векторными операциями первого порядка (в них участвуют только производные первого порядка).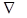 (читается «набла») и называется оператором Гамильтона:
(читается «набла») и называется оператором Гамильтона: .
. на скаляр
на скаляр  или вектор
или вектор  на величины
на величины 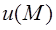 ,
,  ,
, 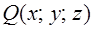 ,
,  понимают как взятие соответствующей частной производной от этих величин.
понимают как взятие соответствующей частной производной от этих величин. .
. .
. .
. ,
, 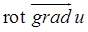 ,
,  ,
,  ,
,  . Понятно, что, например, операция
. Понятно, что, например, операция  не имеет смысла, так как
не имеет смысла, так как 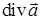 - есть скаляр.
- есть скаляр.
 .
. ,
, , так как векторное произведение двух одинаковых векторных полей равно нулевому вектору. Это означает, что поле градиента есть поле безвихревое.
, так как векторное произведение двух одинаковых векторных полей равно нулевому вектору. Это означает, что поле градиента есть поле безвихревое. .
. , так как смешанное произведение трех векторов, из которых два одинаковых, равно нулю.
, так как смешанное произведение трех векторов, из которых два одинаковых, равно нулю. .
. называется соленоидальным или трубчатым в области
называется соленоидальным или трубчатым в области  , если в каждой точке этой области
, если в каждой точке этой области  .
. поток вектора через любую замкнутую поверхность равен нулю. Соленоидальное поле не имеет источников и стоков.
поток вектора через любую замкнутую поверхность равен нулю. Соленоидальное поле не имеет источников и стоков.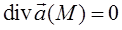 , то существует такое поле
, то существует такое поле  , что
, что  . Вектор
. Вектор  называется векторным потенциалом поля
называется векторным потенциалом поля 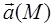 .
.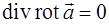 , то поле ротора любого векторного поля
, то поле ротора любого векторного поля  является соленоидальным.
является соленоидальным.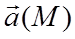 поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение, называемое интенсивностью трубки.
поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение, называемое интенсивностью трубки.


