
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криволинейный интеграл первого рода, формула его вычисления.
Тройной интеграл Понятие тройного (а в дальнейшем – т-мерного) интеграла вводится по аналогии с двойным интегралом. Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части Δvi, считая объем каждой части равным Δvi, и составим интегральную сумму вида где точка Pi принадлежит Δvi. Пусть ρ – наибольшее расстояние между двумя точками любой части области V. Определение 7.3. Предел при
Замечание 1. Условие непрерывности подынтегральной функции не является обязательным для существования кратного (двойного, тройного и т.д.) интеграла, но исследование вопросов, связанных с интегрированием разрывных функций, выходит за рамки нашего курса. Замечание 2. Все сформулированные ранее свойства двойного интеграла можно распространить на тройной интеграл. Замечание 3. Подобным образом можно дать определение интеграла любой кратности, рассматривая функцию п переменных, заданную в замкнутой области п-мерного пространства. Основные свойства тройного интеграла Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства: 1
2
3
4.Если
5.Если область U является объединением двух непересекающихся областей U1 и U2, то
6.Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:
где V - объем области интегрирования U. 1. Теорема о среднем значении тройного интеграла.
где V - объем области U.
Криволинейный интеграл первого рода, формула его вычисления. Определение Пусть кривая C описывается векторной функцией Если на кривой C определена скалярная функция F, то интеграл
Криволинейный интеграл
Свойства криволинейного интеграла первого рода. 1. Линейность: 2. Аддитивность: если 3. Монотонность: если 4. Теорема о среднем для непрерывной вдоль Очевидно, что: 5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: 6. Криволинейный интеграл первого рода не зависит от параметризации кривой.
Криволинейный интеграл второго рода и формула его вычисления. Связь с криволинейным интегралом первого рода. Пусть АВ – непрерывная кривая в пространстве XYZ (или на плоскости ХОY), а точка P(x, y, z) – произвольная функция, определенная на этой кривой. Разобьем кривую точками
Определение. Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменнойх от функции P(x, y, z) по кривой АВ в направлении от А к В.
Криволинейный интеграл второго рода, т.е. интеграл по координатам отличается от криволинейного интеграла первого рода, т.е. по длине дуги тем, что значение функции при составлении интегральной суммы умножается не на длину частичной дуги, а на ее проекцию на соответствующюю ось. (В рассмотренном выше случае – на ось ОХ). Вычисление Пусть
Если обозначить за
Формулировка Пусть C — положительно ориентированная кусочно-гладкая замкнутая кривая на плоскости, а D — область, ограниченная кривой C. Если функции На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая C замкнута. Условие Эйлера.
Комплексные числа. Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается
Конечномерный случай Ортогональный базис — базис, составленный из попарно ортогональных векторов. Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами. Последнее удобно записывается при помощи символа Кронекера: то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности. Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы). Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически. Коэффициенты в разложении вектора по ортогональному базису: Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора
Аналогичные соотношения имеют место и для бесконечномерного случая Бесконечномерный случай Ортогональный базис — система попарно ортогональных элементов
называемого рядом Фурье элемента Необходимым и достаточным условием того, чтобы ортонормированная система Гильбертово пространство, имеющее ортонормированный базис, является сепарабельным, и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис. Если задана произвольная система чисел
Тройной интеграл Понятие тройного (а в дальнейшем – т-мерного) интеграла вводится по аналогии с двойным интегралом. Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части Δvi, считая объем каждой части равным Δvi, и составим интегральную сумму вида
где точка Pi принадлежит Δvi. Пусть ρ – наибольшее расстояние между двумя точками любой части области V. Определение 7.3. Предел при
Замечание 1. Условие непрерывности подынтегральной функции не является обязательным для существования кратного (двойного, тройного и т.д.) интеграла, но исследование вопросов, связанных с интегрированием разрывных функций, выходит за рамки нашего курса. Замечание 2. Все сформулированные ранее свойства двойного интеграла можно распространить на тройной интеграл. Замечание 3. Подобным образом можно дать определение интеграла любой кратности, рассматривая функцию п переменных, заданную в замкнутой области п-мерного пространства. Основные свойства тройного интеграла Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства: 1
2
3
4.Если
5.Если область U является объединением двух непересекающихся областей U1 и U2, то
6.Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:
где V - объем области интегрирования U. 1. Теорема о среднем значении тройного интеграла.
где V - объем области U.
Криволинейный интеграл первого рода, формула его вычисления. Определение Пусть кривая C описывается векторной функцией Если на кривой C определена скалярная функция F, то интеграл Криволинейный интеграл
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.87.144 (0.008 с.) |
 (7.10)
(7.10)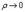 интегральных сумм (7.10), не зависящий от способа разбиения области V, называется тройным интегралом от функции f(x, y, z) по области V:
интегральных сумм (7.10), не зависящий от способа разбиения области V, называется тройным интегралом от функции f(x, y, z) по области V:
 (7.11)
(7.11)

 , где k - константа;
, где k - константа; в любой точке области U, то
в любой точке области U, то  ;
; ;
;
 U, такая, что
U, такая, что
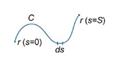
 , где переменная s представляет собой длину дуги кривой (рисунок 1).
, где переменная s представляет собой длину дуги кривой (рисунок 1). называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как 
 существует, если функция F непрерывна на кривой C.
существует, если функция F непрерывна на кривой C. 

 в одной точке, то
в одной точке, то 
 на
на  , то
, то 
 функции
функции  :
: 

 .
. на конечное число частичных дуг. И рассмотрим сумму произведений значений функции в каждой точке на длину соответствующей частичной дуги.
на конечное число частичных дуг. И рассмотрим сумму произведений значений функции в каждой точке на длину соответствующей частичной дуги. ;
; 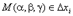

 определена и интегрируема вдоль кривой
определена и интегрируема вдоль кривой  ,
, ,
, .
. единичный вектор касательной к кривой
единичный вектор касательной к кривой 


 ,
,  определены в области D и имеют непрерывные частные производные
определены в области D и имеют непрерывные частные производные  ,
,  , то
, то 






 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма  , где
, где  и
и  — вещественные числа,
— вещественные числа,  — мнимая единица
— мнимая единица
 ), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой. можно найти так:
можно найти так:  .
. квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:
квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису: 
 гильбертова пространства
гильбертова пространства  такая, что любой элемент
такая, что любой элемент  однозначно представим в виде сходящегося по норме ряда
однозначно представим в виде сходящегося по норме ряда 
 . Часто базис
. Часто базис  , и тогда он называется ортонормированным базисом. В этом случае числа
, и тогда он называется ортонормированным базисом. В этом случае числа  , называются коэффициентами Фурье элемента
, называются коэффициентами Фурье элемента  .
. была базисом, является равенство Парсеваля.
была базисом, является равенство Парсеваля. такая, что
такая, что  , то в случае гильбертова пространства с ртонормированным базисом
, то в случае гильбертова пространства с ртонормированным базисом  ряд
ряд  — сходится по норме к некоторому элементу
— сходится по норме к некоторому элементу  . Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству
. Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству  (теорема Рисса — Фишера).
(теорема Рисса — Фишера).


