
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная, неопределённый интеграл и их свойства.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Первообразная, неопределённый интеграл и их свойства. Опр F(x) – первообр для f(x) на некот промежутке, если на этом промеж F(x) – дифф и F’(x)=f(x) Св-ва первообр: 1)Если F(x) – первообр для f, то F(x)+C – также первообр 2)Если F(x) – первообр для f, x?X, то любая др первообр для f на том же промеж будет F(x)+C 3)Разность между V 2мя первообр для f(x) на промеж = С Опр Неопр инт-л от f на некот промеж наз-ся мн-во всех первообр для f на этом промеж, и обозн Св-ва неопр инт-ла: 1) 2) 3)
2.Таблица основных интегралов 1)∫A(x)dx=Ax+C; 2)∫xαdx=((xα+1)/(α+1))+C; 3)∫dx/x=ln|x|+C; 4)∫axdx=ax/lna; 5)∫sinxdx=-cosx+C; 6)∫cosxdx=sinx+C; 7)∫dx/cos2x=tgx+C; 8)∫dx/sin2x=-ctgx+C; 9)∫shxdx=chx+C; 10)∫chxdx=shxdx+C; 11)∫dx/ch2x=thx+C; 12) ∫dx/sh2x=-cthx+C; 13)∫dx/(x2+1)=arctgx+C; 14)∫dx/(x2-a2)=(1/2a)*ln|(x-a)/(x+a)|; Методы разложения и внесения под знак дифференциала. Метод разложения Интеграл от лин комбин конечного числа инт ф-ий равен той же комбинации инт-лов от инт ф-ий Const множитель можно выносить за знак диф-ла Метов внесения под знак диф-ла
Замена переменной в неопределённом интеграле. Т. Пусть x?[a;b]
5.Метод интегрирования по частям.
Разложение рациональной функции на простые дроби. Первообразная любой рац ф-ии Интегрирование рациональных функций.
Первообразная любой рациональой функции Метод Остроградского метод выделения рациональной части неопределенного интеграла от рациональной дроби, знаменатель которой — многочлен степени n с кратными корнями, а числитель — многочлен степени m
Интегрирование некоторых тригонометрических выражений. a)
б)
в)
Интегрирование дробно-линейных иррациональностей.
Если Подстановки Эйлера
1) a>0: 2) c>0: 3) a<0, c<0, D>0, x1<x<x2: Выделение алгебраической части интеграла Ф-ия наз алгебраической, если в D(f) она обладает тождеству вида:pk(x)[f(x)]k+ pk-1(x)[f(x)]k-1+…+ p1(x)f(x)+ p0(x)=0, где n>=1, nєZ, pk, pk-1,…,p0,-некоторые многочлены, Pk(x)≠0. Подинтегральную ф-ию
Интегрирование дифференциальных биномов
1) p?Z Привести m и n к общ знаменателю λ(m=m’/ λ, n=n’/ λ)
2) (m +1)/n? Z
3) p+(m+1)/n? Z
Понятие определённого интеграла Римана. Необходимое условие интегрируемости. Опр Ф-ия f:[a;b]->R наз-ся инт-ой в смысле Римана на отрезке [a;b], если сущ конечный предел I интегральных сумм Условие: Если функция интегрируется в смысле Римана на отрезке, то она ограничена на этом отрезке. НО не всякая ф-ия, ограниченная на отрезке, интегрируема на нем в смысле Римана.
Суммы Дарбу и их св-ва Опр Нижней и верхней суммами Дарбу ф-ии f[a;b]->R, построенные для разбиения Т называются соответственно суммы Св-ва: 1)
2) При измельчении разбиения Т нижняя сумма только увеличивается, верхняя – только уменьшается 3) Нижняя сумма не превосходит верхней, даже если они построены для разных разбиений 4) Критерий Дарбу. Для интегрируемости ограниченной f[a;b]->R в смысле Римана на отрезке [a;b] ó чтобы выполнялось условие Понятие о критерии Лебега. Опр. Покрытие мн-ва Е – семейство мн-ва
Опр. Мн-во счётное, если можно установить взаимооднознач соотношение между его элементами Опр. Мн-во ЕcR имеет лебегову меру ноль, если Т. Для того, чтобы огр ф-ия f:[a;b]->R была инт-ма в смысле Римана ó чтобы мн-во всех её точек имело лебегову меру ноль. Сл-вие Ф-ия, имеющая на отрезке конечное мн-во точек разрыва инт-ма в смысле Римана на это отрезке Сл-вие Изменение значений ф-ии f:[a;b]->R на конечном мн-ве точек не влияет ни на инт-ость ф-ии, ни на величину
Аддитивность инт-ла Римама Т(аддитивность) Если f by-на на [a;b], то
Формула Ньютона-Лейбница Т. Если f:[a,b]->R интегрирована на [a,b] и на этом отрезке сущ первообразная F ф-ии f, то справедливо равенство: Существование первообразных Т. Непрерывн на отр-ке ф-ия имеет первообразную на этом отр-ке. Т. Пусть ф-ия f(x) инт-ма на [a;b], тогда инт-л с перемен верх пределом F(x)=
Квадрируемые фигуры Опр Нижняя площадь фигуры А - Опр Верхняя площадь фигуры А -
Опр Фигура AcR2 наз-ся квадрируемой, если её нижняя и верхняя площади совпадают. В этом случае
Основные понятия связанные с плоскими кривыми Опр. Плоской кривой в Опр. Две кривые
наз-ся совпадающими, если 1) 2) Опр. Носителем (графиком) кривой (1) наз-ся геом. образ этой кривой, т.е. мн-во точек Опр. Точки плоскости Опр. Точки
Основные классы кривых |Г| - носитель кривой Г Опр Кривая называется простой или жордановой, если Опр Кривая Опр Кривая Опр Пусть Опр Кривая называется спрямляемой, если множество длин
Производная по направлению. Опр. Пусть Е – открытое мн-во в Rn и Т. Пусть
Основные понятия числовых рядов. Опр. Числ. ряд – посл-ть конечных сумм спец вида Осн.понятия: 1)общий член 2)частичная сумма 3)остаток 4)отрезок 5)знакопост 6)знакоположит/знакоотриц 7)знакопеременный
Признаки Куммера и Раабе. Т. (Пр-к Куммера).Пусть ∑an- знакаположительный ряд и
Т. (Пр-к Раабе).Пусть сущ-ет конечный или
Признаки Бертрана и Гаусса. Т. (Пр-к Бертрана).Пусть для знакоположительного ряда ∑an сущ-ет конечный или Т.(Пр-к Гаусса). Пусть ∑an- знакаположительный ряд, пусть сущ-ют λ и μ такие, что отношение
Первообразная, неопределённый интеграл и их свойства. Опр F(x) – первообр для f(x) на некот промежутке, если на этом промеж F(x) – дифф и F’(x)=f(x) Св-ва первообр: 1)Если F(x) – первообр для f, то F(x)+C – также первообр 2)Если F(x) – первообр для f, x?X, то любая др первообр для f на том же промеж будет F(x)+C 3)Разность между V 2мя первообр для f(x) на промеж = С Опр Неопр инт-л от f на некот промеж наз-ся мн-во всех первообр для f на этом промеж, и обозн Св-ва неопр инт-ла: 1) 2) 3)
2.Таблица основных интегралов 1)∫A(x)dx=Ax+C; 2)∫xαdx=((xα+1)/(α+1))+C; 3)∫dx/x=ln|x|+C; 4)∫axdx=ax/lna; 5)∫sinxdx=-cosx+C; 6)∫cosxdx=sinx+C; 7)∫dx/cos2x=tgx+C; 8)∫dx/sin2x=-ctgx+C; 9)∫shxdx=chx+C; 10)∫chxdx=shxdx+C; 11)∫dx/ch2x=thx+C; 12) ∫dx/sh2x=-cthx+C; 13)∫dx/(x2+1)=arctgx+C; 14)∫dx/(x2-a2)=(1/2a)*ln|(x-a)/(x+a)|;
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.81 (0.01 с.) |

 , где F(x) – любая первообр для f, C=const
, где F(x) – любая первообр для f, C=const



 и отобр
и отобр  – диф-ема и биективна. Тогда
– диф-ема и биективна. Тогда  , где
, где 
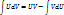
 выражается через рац ф-ии, а также ln и arctg. Рац часть первообразной, будучи приведена к общему знаменателю, должна в качестве такового иметь произведение всех сомножителей, на которые раскладывается многочлен Q(x), только с кратностями, на единицу меньшими, чем кратность их вхождения в разложение Q(x).
выражается через рац ф-ии, а также ln и arctg. Рац часть первообразной, будучи приведена к общему знаменателю, должна в качестве такового иметь произведение всех сомножителей, на которые раскладывается многочлен Q(x), только с кратностями, на единицу меньшими, чем кратность их вхождения в разложение Q(x). , где
, где
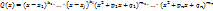
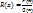 выражается через рациональные функции, а также трнсцендентные функции
выражается через рациональные функции, а также трнсцендентные функции  и
и  .
. n-1. Согласно этому методу,
n-1. Согласно этому методу,  , где многочлены Q1, Q2, P1, P2 имеют степени соответственно n1, n2, m1, m2, такие что n1 + n2 = n, m1
, где многочлены Q1, Q2, P1, P2 имеют степени соответственно n1, n2, m1, m2, такие что n1 + n2 = n, m1  , следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P1(x) и P2(x).
, следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P1(x) и P2(x).  :
:
 или
или  где
где  – рациональная функция:
– рациональная функция: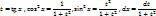
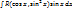 или
или 
 или
или  :
:  и
и 

 , то
, то  ,
, 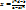 , y=t.
, y=t.



 алгебр преобраз всегда можно представить в виде суммы:R1(x)/
алгебр преобраз всегда можно представить в виде суммы:R1(x)/  +R2(x), где R1(x), R2(x) –рац ф-ии.∫ R(x,
+R2(x), где R1(x), R2(x) –рац ф-ии.∫ R(x,  dx. Разложив рац R1(x) на сумму многочленов pr(x) элем-ных дробей приходим к инт-лам след 3х видов:а)∫Pr(x)/
dx. Разложив рац R1(x) на сумму многочленов pr(x) элем-ных дробей приходим к инт-лам след 3х видов:а)∫Pr(x)/  dx; б)∫1/((x-α)k
dx; б)∫1/((x-α)k 
 Это инт-л от др-лин иррац => далее t=
Это инт-л от др-лин иррац => далее t= 

 , λ – знаменатель p.
, λ – знаменатель p. 
 . λ – знаменатель p.
. λ – знаменатель p. 
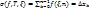 при
при  , т.е.
, т.е.  . Этот предел наз-ся инт-лом Римана для f на [a;b] и обозн
. Этот предел наз-ся инт-лом Римана для f на [a;b] и обозн 




 (эти числа – верхн и нижн инт-лы от f[a;b]->R)
(эти числа – верхн и нижн инт-лы от f[a;b]->R) или что тоже самое
или что тоже самое  где
где  - колебание функции на отрезке
- колебание функции на отрезке 
 , что EcV, т.е.
, что EcV, т.е. 
 такое покрытие мн-ва Е с конечным или счётным семейством интервалов, что сумма длин любого кол-ва интервалов
такое покрытие мн-ва Е с конечным или счётным семейством интервалов, что сумма длин любого кол-ва интервалов 
 она инт-на на [a;c] и [c;b]:
она инт-на на [a;c] и [c;b]: 

 явл ф-ей непрер на [a;b]
явл ф-ей непрер на [a;b] по всем P0 содержащ в A:P0 c A
по всем P0 содержащ в A:P0 c A по всем
по всем 



 назы-ся любое непрерывное отображение
назы-ся любое непрерывное отображение  отрезка
отрезка  или
или  (1)
(1)
 непрер. строго возраст ф-ция
непрер. строго возраст ф-ция 

 ;
; 
 по всем
по всем 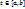
 наз-ся началом и концом (1), если
наз-ся началом и концом (1), если  , то кривая наз-ся замкнутой, иначе разомкнутой.
, то кривая наз-ся замкнутой, иначе разомкнутой. , которым соотв.
, которым соотв.  несколько точек
несколько точек  – для замкнуто кривой.
– для замкнуто кривой. – взаимнооднозначн. (для замкн. кривой –
– взаимнооднозначн. (для замкн. кривой – 
 – разбиение отрезка [a,b], тогда ломаная с паследоват. вершинами
– разбиение отрезка [a,b], тогда ломаная с паследоват. вершинами  называется вписанной в кривую Г
называется вписанной в кривую Г всевозможных ломанных вписанных в кривую ограничено сверху. В этом случае конечн. верхняя граница
всевозможных ломанных вписанных в кривую ограничено сверху. В этом случае конечн. верхняя граница  называется длиной кривой:
называется длиной кривой:  , где sup берется по всем разбиениям Т [a,b]
, где sup берется по всем разбиениям Т [a,b] – скал ф-ия. Пусть далее
– скал ф-ия. Пусть далее  – некот единичный в-р, тогда производная по направлению
– некот единичный в-р, тогда производная по направлению  наз число
наз число  , если lim сущ-ет и конечен.
, если lim сущ-ет и конечен. открытое мн-во и скал ф-ия
открытое мн-во и скал ф-ия  , тогда в этой точке сущ производная по любому направл.
, тогда в этой точке сущ производная по любому направл.  и верно рав-во
и верно рав-во 

 постр по к-либо числ посл-ти
постр по к-либо числ посл-ти 
 -некотор посл-ть положит чисел, пусть далее Kn=Cn
-некотор посл-ть положит чисел, пусть далее Kn=Cn  -Cn+1,n=1,2,… перемен Куммера для ряда ∑an постр по данной посл-ти (Cn), тогда: 1)Если
-Cn+1,n=1,2,… перемен Куммера для ряда ∑an постр по данной посл-ти (Cn), тогда: 1)Если  такое δ>0, что начиная с некоторого номера Kn
такое δ>0, что начиная с некоторого номера Kn  δ, то ряд ∑an сх-ся; 2)если начиная с некоторого номера
δ, то ряд ∑an сх-ся; 2)если начиная с некоторого номера  0 и при этом ∑
0 и при этом ∑  расх-ся, то ряд ∑an также расх-ся.
расх-ся, то ряд ∑an также расх-ся. предел R=lim n(
предел R=lim n( +O(
+O( ) при n→+∞, тогда ряд ∑an: 1)сх-ся, λ>1 или
) при n→+∞, тогда ряд ∑an: 1)сх-ся, λ>1 или  ; 2)расх-ся, λ<1 или
; 2)расх-ся, λ<1 или  ; 3)сомнительных случаев нет.
; 3)сомнительных случаев нет.


