
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Длина гладкой кривой. Спрямляемость кусочно-гладкой кривойСодержание книги
Поиск на нашем сайте
Т Гладкая кривая
T Кусочно гладкая кривая
где
Площадь поверхности вращения Опр Поверхность вращения графика ф-ции Если
39. Евклидово пространство в Опр Пр-во Опр Евклидово расстояние (метрика) в
Теор ф-ла(1) удовлетв всем условиям метрики Опр Длиной (евклидовой мерой) в-ра Опр Скалярное произведение векторов (
41. Основные топологические понятия в Опр Окрестностью т.
Опр Мн-во Опр Опр Мн-во Опр т. внутренней, если содерж в Е с некот своей окр-тью внешней, если явл-ся внутренней для СЕ граничной, если ни внутр, ни внешняя предельной, если изолированной, если Опр мн-во Теор мн-во
40. Сходимость в Опр Посл-ть в-ров из
Теор Сходимость посл-ти векторов равносильно их покоординатной сх-ти:
Теор(крит Коши) Посл-ть в-ров
Следств Евклидово пр-во Кратные пределы отображений. Теорема о покоординатной сходимости Опр Пусть
Повторный предел. Теорема о существовании повторного предела. Повторными пределами для
Теор (о сущ-ии повтор предела) Пусть для скалярной ф-ий 2-х перемен в некоторой точке 44.Непрерывность отображений из Опр Ф-ция
Локальные свойства: 1) 2) 3) Если g Глобальные свойства непрерывных отображений 1) Если отображение 2) Если отображение 3) Если ф-ция 4) Если ф-ция
46.Линейные отображения из Rn в Rm. Линейное отображение векторного пр-ва Х в Y наз-ся линейным над полем R, если:
Т. Отображение Т. Для любого линейного Линейное отобр
47 Дифференцируемые отображения из Rn в Rm. Простейшие свойства Опр Отобр Св-ва: 1) Если отобр 2) Если отобр Дифференцируемость композиции отображений. Пусть
Теорема о покоординатной дифференцируемости отображения Диф-ость отобр
Частные производные. Теорема о смешанных производных. ОПР Частной произв 1го порядка скал ф-ии Т. (о смешанных произв) Если смешанные частные производные
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.201.71 (0.006 с.) |

 спрямляема, и для ее длины
спрямляема, и для ее длины  справедл. формула:
справедл. формула:
 спрямляема, и ее длину можно вычислить
спрямляема, и ее длину можно вычислить
 – отрезки, на которых кривая гладкая.
– отрезки, на которых кривая гладкая. вокруг Ох наз-ся квадрируемой, если мн-во
вокруг Ох наз-ся квадрируемой, если мн-во  площадей всех поверхносей ломаных линий, вписанных в это графикограничено сверху. Площадь фигуры вращения –
площадей всех поверхносей ломаных линий, вписанных в это графикограничено сверху. Площадь фигуры вращения – 
 на [a,b] имеет непрерывн произв, то
на [a,b] имеет непрерывн произв, то 
 (основные понятия)
(основные понятия) наз-ся декарт произв
наз-ся декарт произв  -штук), т.е. мн-во всех упорядоченных наборов
-штук), т.е. мн-во всех упорядоченных наборов 
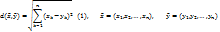
 наз-ся число
наз-ся число  где
где  – начало координат в
– начало координат в  наз-ся число (
наз-ся число (

 наз-ся мн-во
наз-ся мн-во ,
, 
 наз-ся открытым, если оно содержит каждую свою точку вместе с некоторой окрестностью.
наз-ся открытым, если оно содержит каждую свою точку вместе с некоторой окрестностью. – замкн. если
– замкн. если  – открыто в
– открыто в  наз-ся сферой с центром в т.
наз-ся сферой с центром в т.  и радиусом
и радиусом  . Замкнутое.
. Замкнутое. по отношению к мн-ву
по отношению к мн-ву  – бесконечн множество
– бесконечн множество
 наз-ся замыканием мн-ва
наз-ся замыканием мн-ва  и обозначается
и обозначается 
 – замкнуто в
– замкнуто в 

 наз-ся сходящейся к вектору
наз-ся сходящейся к вектору  , если
, если 


 сх-ся в
сх-ся в 
 - предельная точка
- предельная точка  , явл-ся пределом
, явл-ся пределом  в т.
в т. 




 в точке
в точке  , предельной для Е, наз-ся пределы по мн-ву Е вида:
, предельной для Е, наз-ся пределы по мн-ву Е вида:
 интеграл, а также предел по одной из переменных, тогда в этой точке сущ-ет и соотв двойной предел.
интеграл, а также предел по одной из переменных, тогда в этой точке сущ-ет и соотв двойной предел. в
в  . Локальные свойства.
. Локальные свойства. – непрерывна в точке
– непрерывна в точке  , если
, если


 - непрер
- непрер 

 – непрерывно в
– непрерывно в  , a
, a 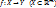 - непрерывно в
- непрерывно в  , причем
, причем  , то определено отображение
, то определено отображение  и оно непрерывно в точке
и оно непрерывно в точке 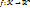 - непрерывно на компакте
- непрерывно на компакте  , то оно равномерно непрерывно на
, то оно равномерно непрерывно на  .
.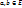 значения
значения  , то
, то  .
.
 линейно т. и т. т., когда линейными явл-ся все его коорд ф-ии.
линейно т. и т. т., когда линейными явл-ся все его коорд ф-ии.
 непрер в любой точке
непрер в любой точке 
 , называется дифф-мым в точке
, называется дифф-мым в точке  , если для него сущ-ет такое отображение
, если для него сущ-ет такое отображение  , что
, что 
 диф-мо в т.
диф-мо в т.  – откр мн-ва. Пусть далее f:X->Y диф в точке
– откр мн-ва. Пусть далее f:X->Y диф в точке  , а отобр g:Y->Rp диф-мо в т.
, а отобр g:Y->Rp диф-мо в т.  . Тогда композиция g o а диф-ма в т.
. Тогда композиция g o а диф-ма в т.  и справедл рав- во:
и справедл рав- во: 
 равнос диф-сти всех его покоорд ф-ий fk, причём справ-во покоординатное представление диф-ла отобр:
равнос диф-сти всех его покоорд ф-ий fk, причём справ-во покоординатное представление диф-ла отобр:  , где
, где  – стандартный базис в
– стандартный базис в  .
. 
 по переменной
по переменной  в т.
в т.  наз-ся обыкновен произв ф-ии
наз-ся обыкновен произв ф-ии  в т.
в т.  , т.е. предел:
, т.е. предел: 
 и
и  сущ в некот окр-сти в т.
сущ в некот окр-сти в т.  и непр-ны в самой т.
и непр-ны в самой т.  =
= 



