
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейность и монотонность интеграла РиманаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Т(линейность) Если ф-ии Т(монотонность) Если ф-ии
Аддитивность инт-ла Римама Т(аддитивность) Если f by-на на [a;b], то
Интегрируемость модуля функции. Оценка интеграла. Т(об инт-сти модуля) Если Сл-вие(оценка инт-ла) Если Замеч Если f непрер на [a;b], то Интегрируемость произведения функций Т(инт -ость произв ф-ий) Если Т(оценка инт-ла от произв) Пусть выполнены усл: 1) 2) 3) Для некот const m и M, ф-ия удовл нер-вам Первая теорема о среднем для интегралов T. Пусть выполняется условие: 1) 2) хотя бы одна функция (пусть g(x)) меняет знак на [a;b] 3)
Причём кроме того, если f непрерывна на [a;b], то Формула Ньютона-Лейбница Т. Если f:[a,b]->R интегрирована на [a,b] и на этом отрезке сущ первообразная F ф-ии f, то справедливо равенство: Существование первообразных Т. Непрерывн на отр-ке ф-ия имеет первообразную на этом отр-ке. Т. Пусть ф-ия f(x) инт-ма на [a;b], тогда инт-л с перемен верх пределом F(x)=
Замена переменной в определённом интеграле Т. Пусть выполнены условия: 1) f – непрер на [a;b] 2) ф-ия 3) Тогда справедлива ф-ия замены переменной в опр инт-ле Т. (усил вариант замены)Пусть выполняются условия: 1) 2) ф-ия 3) Тогда справедлива формула
Интегралы от чётных, нечётных и периодических функций. Интегрирование по частям. T. Интеграл от чётной интегрируемой функции по симметричному относительно 0 прямоугольнику равен удвоенному интегралу по половине прямоугольника. А интеграл от нечетной функции равен 0:
Т. Пусть f:R->R имеет период Т и интегрируема на каждом отрезке [a;b]cR, тогда интеграл от f по любому отрезку длины T сохраняет const значение: Т. Пусть ф-ии U=U(x) и V=V(x) имеют на отрезке [a;b] инт-мые производные, тогда
29.Открытые и замкнутые множества в R2
Опр Мн-во XcR2 наз-ся открытым в R2, если все точки внутренние, т.е. X=X0 Опр Т.М называется предельной для множества А, если в V ей окрестности U(M) есть беск мн-во точек из А. Предельная точка может принадл или не принадл мн-ву.
Опр Мн-во YcR2 называется замкнутым в R2, если его дополнение CY= R2\Y открыто в R2 или если содержит все свои предельные точки Замкнутое мн-во совпадает со своим замыканием.
Квадрируемые фигуры Опр Нижняя площадь фигуры А - Опр Верхняя площадь фигуры А -
Опр Фигура AcR2 наз-ся квадрируемой, если её нижняя и верхняя площади совпадают. В этом случае
О критериях квадрируемости плоской фигуры (1ый кр. квадр) (2ой кр. квадр) (3ий кр. квадр) Необх и дост, чтобы ее граница была фигура площади 0 Площадь криволинейной трапеции Пусть f:[a;b]→R-неотриц ф-ия.Криволиненой трапецией наз мн-во A={(x,y)єR2:a Т. Если f:[a;b]→R-неотриц инт-ма ф-ия, то криволинейная трапеция квадрируема и её площадь равна: μ(A)= Площадь криволинейного сектора Пусть
Вычисление объемов некоторых тел Пусть
Основные понятия связанные с плоскими кривыми Опр. Плоской кривой в Опр. Две кривые
наз-ся совпадающими, если 1) 2) Опр. Носителем (графиком) кривой (1) наз-ся геом. образ этой кривой, т.е. мн-во точек Опр. Точки плоскости Опр. Точки
Основные классы кривых |Г| - носитель кривой Г Опр Кривая называется простой или жордановой, если Опр Кривая Опр Кривая Опр Пусть
Опр Кривая называется спрямляемой, если множество длин
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 754; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.149.93 (0.011 с.) |

 то при
то при  их лин комбинация
их лин комбинация  также инт-на на [a;b]:
также инт-на на [a;b]: 
 , то вместе с тем и
, то вместе с тем и 
 она инт-на на [a;c] и [c;b]:
она инт-на на [a;c] и [c;b]: 
 то и
то и  , причём модуль инт-ла не превосходит инт-ла модуля.
, причём модуль инт-ла не превосходит инт-ла модуля. , где
, где 



 ,
,  , тогда справедливы оценки: m
, тогда справедливы оценки: m  .
.
 , тогда
, тогда 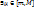 , то
, то


 явл ф-ей непрер на [a;b]
явл ф-ей непрер на [a;b] непр, диф-ма на
непр, диф-ма на 



 также инт на
также инт на 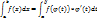



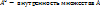


 (граница – замкнутое мн-во)
(граница – замкнутое мн-во) – замыкание мн-ва А (мн-во А + все его предельные точки)
– замыкание мн-ва А (мн-во А + все его предельные точки) по всем P0 содержащ в A:P0 c A
по всем P0 содержащ в A:P0 c A по всем
по всем 



 – квадрируема
– квадрируема 
 x
x 
 . Криволинейным сектором наз. плоская фигура
. Криволинейным сектором наз. плоская фигура  , которая в полярн. системе координат может быть задана
, которая в полярн. системе координат может быть задана 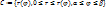 Если
Если 
 – тело, распол. между касающимися его плоскостями
– тело, распол. между касающимися его плоскостями  , - квадрир. Если
, - квадрир. Если  интегрируемо на
интегрируемо на  , то тело
, то тело  - кубируемо и его объем равен интегралу
- кубируемо и его объем равен интегралу
 назы-ся любое непрерывное отображение
назы-ся любое непрерывное отображение  отрезка
отрезка  или
или  (1)
(1)
 непрер. строго возраст ф-ция
непрер. строго возраст ф-ция 

 ;
; 
 по всем
по всем 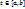
 наз-ся началом и концом (1), если
наз-ся началом и концом (1), если  , то кривая наз-ся замкнутой, иначе разомкнутой.
, то кривая наз-ся замкнутой, иначе разомкнутой. , которым соотв.
, которым соотв.  несколько точек
несколько точек  – для замкнуто кривой.
– для замкнуто кривой. – взаимнооднозначн. (для замкн. кривой –
– взаимнооднозначн. (для замкн. кривой – 
 – разбиение отрезка [a,b], тогда ломаная с паследоват. вершинами
– разбиение отрезка [a,b], тогда ломаная с паследоват. вершинами  называется вписанной в кривую Г
называется вписанной в кривую Г всевозможных ломанных вписанных в кривую ограничено сверху. В этом случае конечн. верхняя граница
всевозможных ломанных вписанных в кривую ограничено сверху. В этом случае конечн. верхняя граница  называется длиной кривой:
называется длиной кривой:  , где sup берется по всем разбиениям Т [a,b]
, где sup берется по всем разбиениям Т [a,b]


