
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условный экстремум. Необходимый и достаточный признаки существования.Содержание книги
Поиск на нашем сайте
Опр Точка 1) 2) 3) 4) Т. (необх пр-к сущ-ния) Для того, чтобы точка
Т. (дост пр-к сущ-ния) Пусть ф-ии
Основные понятия числовых рядов. Опр. Числ. ряд – посл-ть конечных сумм спец вида Осн.понятия: 1)общий член 2)частичная сумма 3)остаток 4)отрезок 5)знакопост 6)знакоположит/знакоотриц 7)знакопеременный
Простейшие операции над рядами. Т. (об умножении членов ряда на число).Если ряд ∑ak сх и λ-число, то ряд ∑λak сх и след рав-во ∑λak=λ∑ak. Т. (о почленном сложении рядов). Если ряды ∑ak и ∑bk сх, то ряд ∑(ak+bk) также сх и справедливо рав-во: ∑(ak+bk)= ∑ak+∑bk. Т. (о группировке членов ряда).Пусть a1+a2+…-4P(числ ряд) и 1 Т. Любая перестановка конечного числа членов ряда не нарушает его свойств сходимости и не нарушает его сумму.
Критерий Коши и другие критерии сходимости для числовых рядов Т. Т. (критерий сх-ти ряда в терминах остатов)Сх-ть ряда ∑ak равносильна сх-ти любого его остатка. В случае сх-ти ряда посл-ть (rn) суммы остатков стремится к 0. Т. (критерий сх-ти ряда с неотриц членами)Сх-ть числ ряда с неотриц членами равнос ограниченности сверху посл-ти его частных сумм. Признаки сравнения для знакоположительных рядов. Т. (Мажорантный признак сравнения). Пусть ∑ak и ∑bk ряды с неотриц членами и ak=O(bk) при k→∞, тогда: 1)Если ряд ∑bk сх-ся, то ряд ∑ak также сх-ся; 2) Если ряд ∑ak расх-ся, то ряд ∑bk также расх-ся. Т. (признак сравнения в предельной форме).Пусть ∑bk и ∑ak-знакополож ряды и существует lim ak/bk=Lє[0;+∞), тогда: 1)При 0<L<+∞ ряды ∑bk и ∑ak оба сх-ся или расх; 2)При L=0 из сх ниж ряда из ∑bk вытекает сх-ть ряда ∑ak; 3)При L=+∞ из расход-ти верхнего ряда ∑ak вытекает расх-ть нижнего ряда ∑bk. Т. (признак сравнения отношения).Пусть сумма ∑ak и ∑bk-знакоположит ряды и для всех вы прав-во:
67. Интегральный признак сходимости для знакоположительных рядов. Следствия. Т. (Интеграл призн Маклорена-Коши).Пусть f:[1;+∞)→R-положит убывающ ф-ия, тогда сходимость числового ряда ∑f(x) равносильна существованию конечного lim f(x) первообразной F(x) для ф-ии f(x). Сл. Для гармонического ряда ∑ Т. (Пр-к Коши(с корнем)). Пусть ∑ak-ряд с неотриц членами, для кот Т. (Пр-к Даламбера).Пусть для знакаположительного ряда ∑ak сущ-ет lim
Признаки Куммера и Раабе. Т. (Пр-к Куммера).Пусть ∑an- знакаположительный ряд и Т. (Пр-к Раабе).Пусть сущ-ет конечный или
Признаки Бертрана и Гаусса. Т. (Пр-к Бертрана).Пусть для знакоположительного ряда ∑an сущ-ет конечный или Т.(Пр-к Гаусса). Пусть ∑an- знакаположительный ряд, пусть сущ-ют λ и μ такие, что отношение
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.254.81 (0.008 с.) |

 – точка лок усл экстремума ф-ии
– точка лок усл экстремума ф-ии  при условии
при условии 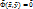 , если сущ
, если сущ 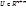 точки
точки  , такая, что для
, такая, что для 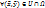 выполнено хотя бы 1 из след нер-в:
выполнено хотя бы 1 из след нер-в: – строгий усл мин
– строгий усл мин - усл мин
- усл мин - строгий усл мах
- строгий усл мах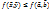 - усл мах
- усл мах была т. усл экстр ф-ии
была т. усл экстр ф-ии  при некот знач
при некот знач  удовл сис-ме уравнений:
удовл сис-ме уравнений:
 и
и  имеют непрер частн произв 2го порядка в окр-сти точки
имеют непрер частн произв 2го порядка в окр-сти точки  и в этой точке Якобиан (опред м-цы Якоби) отличен от 0, тогда наличие усл экстр для ф-ии
и в этой точке Якобиан (опред м-цы Якоби) отличен от 0, тогда наличие усл экстр для ф-ии  постр по к-либо числ посл-ти
постр по к-либо числ посл-ти 
 n1
n1  , т.е любой отрезок ряда может быть сделан сколь угодно малым, начиная с некоторого номера.
, т.е любой отрезок ряда может быть сделан сколь угодно малым, начиная с некоторого номера. , тогда: 1)∑bk сх, тогда ∑ak сх; 2)∑ak расх, тогда ∑bk расх.
, тогда: 1)∑bk сх, тогда ∑ak сх; 2)∑ak расх, тогда ∑bk расх. имеем f(x)=
имеем f(x)=  . Её первообразная F(x)=ln x→+∞, тогда ряд ∑
. Её первообразная F(x)=ln x→+∞, тогда ряд ∑  Sn-1 при f(x)=
Sn-1 при f(x)=  :
:  Более точная ф-ла:
Более точная ф-ла:  ,
,  →0, c=lim(
→0, c=lim( ) наз постоянной Эйлера(с=0,577…) 68. Признаки Коши и Даламбера
) наз постоянной Эйлера(с=0,577…) 68. Признаки Коши и Даламбера =q, тогда: 1)при q<1 ряд сх-ся; 2)при q>1 ряд расх-ся; 3)при q=1 необх дополн исслед ряда.
=q, тогда: 1)при q<1 ряд сх-ся; 2)при q>1 ряд расх-ся; 3)при q=1 необх дополн исслед ряда. =D, тогда: 1)при D<1 ряд сх-ся; 2)при D>1 ряд расх-ся; 3)при D=1 необх дополн исслед ряда.
=D, тогда: 1)при D<1 ряд сх-ся; 2)при D>1 ряд расх-ся; 3)при D=1 необх дополн исслед ряда. -некотор посл-ть положит чисел, пусть далее Kn=Cn
-некотор посл-ть положит чисел, пусть далее Kn=Cn  -Cn+1,n=1,2,… перемен Куммера для ряда ∑an постр по данной посл-ти (Cn), тогда: 1)Если
-Cn+1,n=1,2,… перемен Куммера для ряда ∑an постр по данной посл-ти (Cn), тогда: 1)Если  такое δ>0, что начиная с некоторого номера Kn
такое δ>0, что начиная с некоторого номера Kn  δ, то ряд ∑an сх-ся; 2)если начиная с некоторого номера
δ, то ряд ∑an сх-ся; 2)если начиная с некоторого номера  0 и при этом ∑
0 и при этом ∑  расх-ся, то ряд ∑an также расх-ся.
расх-ся, то ряд ∑an также расх-ся. предел R=lim n(
предел R=lim n( +O(
+O( ) при n→+∞, тогда ряд ∑an: 1)сх-ся, λ>1 или
) при n→+∞, тогда ряд ∑an: 1)сх-ся, λ>1 или  ; 2)расх-ся, λ<1 или
; 2)расх-ся, λ<1 или  ; 3)сомнительных случаев нет.
; 3)сомнительных случаев нет.


