
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение дифференциальных уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ua = URa + UCa, в этом выражении URa, UCa соответственно падение напряжения на резисторе и конденсаторе. Дальнейшее преобразование определяется целью анализа, можно получить уравнение для оценки изменения тока в цепи во времени или уравнение для оценки изменения напряжения на конденсаторе во времени. Остановимся на втором варианте. В этом случае URa = i*Ra, где i - ток в контуре, т.е. ток протекающий по конденсатору. Зависимость тока в конденсаторе от напряжения на конденсаторе определяется выражением
Рассмотрим качественно возможность построения схемы из решающих элементов для решения уравнения описывающего процессы в электрической цепи. Для этой цели дифференциальное уравнение разрешим относительно старшей производной
Сравнивая последние два уравнения видно, что это уравнения совершенно одинаковые по форме записи, только приняты различные обозначения переменных и констант. Подобные уравнения называют изоморфными. Так в первом уравнении Ra и Ca это соответственно резистор и конденсатор электрической цепи, а во втором уравнении R1, R2 и C0 -- это соответственно входные резисторы и конденсатор интегратора. Проведение аналогии состоит в том, что на первый вход интегратора будем подавать напряжение пропорциональное Ua -- напряжению источника в электрической цепи, на второй вход интегратора будем подавать напряжение пропорциональное UC -- напряжению на конденсаторе электрической цепи, а коэффициенты передачи по входам зададим пропорциональными 1/(RaCa). При выполнении указанных условий выходное напряжение интегратора Uвых будет пропорционально напряжению на конденсаторе. Необходимо отметить, что начальные условия задаются начальным зарядом конденсатора обратной связи интегратора, исходя из соотношения UC0|t=0 ≡UC|t=0. Исходя из аналогии можно составлять схему из решающих элементов. Из приведенных рассуждений приходим Как видно на схеме требуется только один интегратор. Этот факт дает возможность сделать оценку, что количество интеграторов определяется порядком решаемого дифференциального уравнения. Так, например, при решении уравнения третьего порядка потребуется три интегратора. В данном изложении не затронуты вопросы количественных соотношений между реальными переменными и их моделирующими переменными. Важная особенность аналогового моделирования состоит в том, что результаты начинаем получать мгновенно после включения решения, так как скорость выполнения вычислительных операций зависит от скорости распространения электромагнитной волны по проводнику. Поэтому характеристика быстродействия аналоговых вычислительных машин не имеет смысла. Триггер Шмитта.
Лекция 12
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 624; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

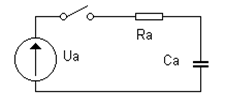 Рассмотрим решение переходного процесса в электрической цепи, состоящей из источника напряжения постоянного тока, резистора и конденсатора (рис.90).
Рассмотрим решение переходного процесса в электрической цепи, состоящей из источника напряжения постоянного тока, резистора и конденсатора (рис.90). После замыкания ключа по цепи протекает ток. Для аналитического описания процесса протекания тока составим для этой цепи уравнение по второму закону Кирхгофа.
После замыкания ключа по цепи протекает ток. Для аналитического описания процесса протекания тока составим для этой цепи уравнение по второму закону Кирхгофа.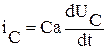 , выполняя подстановку получим дифференциальное описывающее изменение напряжения на конденсаторе.
, выполняя подстановку получим дифференциальное описывающее изменение напряжения на конденсаторе.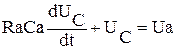 получили дифференциальное уравнение первого порядка, линейное, неоднородное, причем правая часть уравнения представляет собой внешнее возбуждающее воздействие. Так как полученное уравнение первого порядка, то необходимо иметь одно начальное условие, в нашем случае это напряжение на конденсаторе перед замыканием ключа. Возьмем Uc| t-0 = 0.
получили дифференциальное уравнение первого порядка, линейное, неоднородное, причем правая часть уравнения представляет собой внешнее возбуждающее воздействие. Так как полученное уравнение первого порядка, то необходимо иметь одно начальное условие, в нашем случае это напряжение на конденсаторе перед замыканием ключа. Возьмем Uc| t-0 = 0.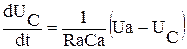 , и затем проинтегрируем,
, и затем проинтегрируем,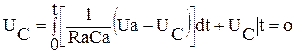 . Ниже напишем уравнение для интегросумматора.
. Ниже напишем уравнение для интегросумматора.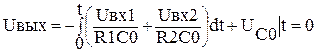 .
. к выводу, что для решения нам необходим интегросумматор на два входа, причем при изображении схемы на входах и выходе решающего элемента укажем переменные из уравнения, описывающего электрическую схему. Понятно, что для получения правильного решения знаки переменных должны соответствовать знакам в уравнении, но требуется учитывать, что решающий элемент обладает способностью изменять знак выходной переменной, поэтому перед расстановкой знаков необходимо правую часть уравнения умножить на -1, и
к выводу, что для решения нам необходим интегросумматор на два входа, причем при изображении схемы на входах и выходе решающего элемента укажем переменные из уравнения, описывающего электрическую схему. Понятно, что для получения правильного решения знаки переменных должны соответствовать знакам в уравнении, но требуется учитывать, что решающий элемент обладает способностью изменять знак выходной переменной, поэтому перед расстановкой знаков необходимо правую часть уравнения умножить на -1, и 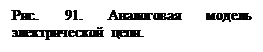 полученные знаки расставить на схеме. Далее точки схемы, имеющие одинаковые обозначения и знаки должны быть соединены. Если в схеме имеются точки с одинаковыми переменными, но разными знаками необходимо устанавливать инверторы с коэффициентами передачи -1, для согласования знаков. Схема электронной модели электрической цепи, построенной по рассмотренным принципам, показана на рис.91.
полученные знаки расставить на схеме. Далее точки схемы, имеющие одинаковые обозначения и знаки должны быть соединены. Если в схеме имеются точки с одинаковыми переменными, но разными знаками необходимо устанавливать инверторы с коэффициентами передачи -1, для согласования знаков. Схема электронной модели электрической цепи, построенной по рассмотренным принципам, показана на рис.91.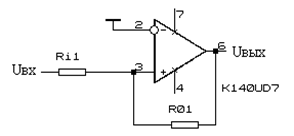 Рассмотренные до сих пор схемы с операционными усилителями использовались с применением отрицательной обратной связи. Но применение положительной обратной связи приводит к появлению схем с особыми свойствами. К ним относятся триггеры Шмитта, схема одного из них приведена на рис.. Изображенная схема предполагает симметричное питание.
Рассмотренные до сих пор схемы с операционными усилителями использовались с применением отрицательной обратной связи. Но применение положительной обратной связи приводит к появлению схем с особыми свойствами. К ним относятся триггеры Шмитта, схема одного из них приведена на рис.. Изображенная схема предполагает симметричное питание. В цепи обратной связи установлен резистор R01 а во входной цепи -- Ri1. Инвертирующий вход подключен к общему проводу. Рассмотрим работу данной схемы.
В цепи обратной связи установлен резистор R01 а во входной цепи -- Ri1. Инвертирующий вход подключен к общему проводу. Рассмотрим работу данной схемы.


