
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное неинвертирующее включение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Схема основного не инвертирующего включения приведена на рис.85. Как видно из схемы сохранилась цепь отрицательной обратной связи. Но левый по схеме вывод входного резистора R1 подключен к общему проводу, а входное напряжение подается на неинвертирующий вход. Выполним вывод уравнения для определения выходного напряжения. Определим напряжение в точке а. Ua = U¯ = (Uвых*R1)/(R0 + R1). Напряжение на неинверти Выходное сопротивление схемы определяется также как и в предыдущей схеме. Входное сопротивление схемы значительно больше, чем в предыдущем случае, так как оно определяется входным током операционного усилителя. Если используется ОУ 140УД7 с входным током 200нА, то при Uвх = 10в получим Rвхос = 10В/200нА = 50 мегом.
Эта схема характеризуется тем, что: - для нее выполняется соотношение Uвых = Uвх, т.е. она является повторителем напряжения, -она имеет высокое входное сопротивление, -она имеет низкое выходное сопротивление. В соответствии с указанными особенностями эта схема часто используется в качестве преобразователя импеданса (полного сопротивления). Выводы основных соотношений для включений ОУ выполнены на постоянном токе (с целью упрощения), однако полученные результаты могут быть распространены и на частотную область. Для частотной области будем иметь: - - не инвертирующее включение Приведенные выражения позволяют просто получить выражения передаточных функций, которые подтверждают ранее полученный вывод о том, что при использовании усилителей с большим коэффициентом усиления передаточная функция определяется цепь обратной связи. Передаточные функции будут иметь вид - для инвертирующего включения - для не инвертирующего включения Следовательно, если известна схема цепи обратной связи, то можно определить полные сопротивления и передаточную функцию. Решающие элементы аналоговых вычислительных машин (АВМ). Под решающими элементами будем понимать электронные устройства, предназначенные для выполнения вычислительных операций над переменными АВМ и построенные с применением ОУ. Необходимость применения ОУ обоснована тем, что только большое значение коэффициента усиления (десятки, сотни тысяч) позволяет определить передаточную функцию только цепью обратной связи. Причем обратная связь должна быть отрицательной для получения устойчивой работы.
Сумматор.
Интегратор. Если в схеме сумматора резистор обратной связи R01 заменить на конденсатор, то получаем новый решающий элемент, выполняющий операцию интегрирования – интегратор (рис.88). Определим зависимость между входным и выходным напряжениями. Для достижения этой цели составим уравнение по первому закону Кирхгофа для точки a. При этом будем считать, что резистор и конденсатор выбраны таким образом, что ток протекающий через них значительно (например, в 1000 раз) больше входного тока операционного усилителя. Это дает нам возможность сделать допущение – пренебречь входным током операционного усилителя. При выводе воспользуемся законом Ома для участка цепи.
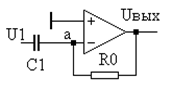
Дифференциатор. Если в схеме интегратора резистор и конденсатор поменять местами, то получим элемент выполняющий операцию дифференцирования – дифференциатор (рис.). Составляя уравнение по первому закону Кирхгофа для точки а, получим
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.011 с.) |

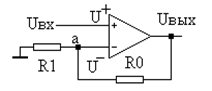 рующем входе равно входному напряжению U+ = Uвх. Рассмотрим основное уравнение операционного усилителя Uвых = Ку*(U+ - U¯). Если правую и левую части уравнения поделим на Ку, то получим Uвых / Ку = (U+ - U¯) → 0. Это близко к истине, так как Ку величина большая и теоретически стремиться к бесконечности, Uвых конечна и не может быть больше напряжения питания. Отсюда получаем U+ = U¯,
рующем входе равно входному напряжению U+ = Uвх. Рассмотрим основное уравнение операционного усилителя Uвых = Ку*(U+ - U¯). Если правую и левую части уравнения поделим на Ку, то получим Uвых / Ку = (U+ - U¯) → 0. Это близко к истине, так как Ку величина большая и теоретически стремиться к бесконечности, Uвых конечна и не может быть больше напряжения питания. Отсюда получаем U+ = U¯,  Uвх = (Uвых*R1)/(R0 + R1). Полученное выражение разрешим относительно выходного напряжения
Uвх = (Uвых*R1)/(R0 + R1). Полученное выражение разрешим относительно выходного напряжения 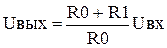 . В данном случае коэффициент передачи Ксос = (R0 + R1)/R0, и не может быть меньше единицы.
. В данном случае коэффициент передачи Ксос = (R0 + R1)/R0, и не может быть меньше единицы.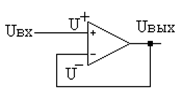 Модификацией основного не инвертирующего включения является схема без резистивной цепи обратной связи показанная на рис.83.
Модификацией основного не инвертирующего включения является схема без резистивной цепи обратной связи показанная на рис.83. инвертирующее включение
инвертирующее включение 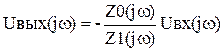 ,
,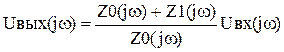 .
.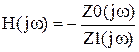 ,
,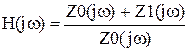 .
.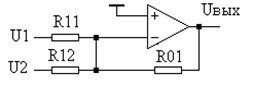 Сумматор – решающий элемент, выполняющий операцию суммирования. Схема сумматора показана на рис.87. По известной методике сделаем вывод зависимости выходного напряжения в зависимости от входных напряжений.
Сумматор – решающий элемент, выполняющий операцию суммирования. Схема сумматора показана на рис.87. По известной методике сделаем вывод зависимости выходного напряжения в зависимости от входных напряжений.
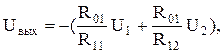 обобщая полученный результат для схемы с N входами, будем иметь
обобщая полученный результат для схемы с N входами, будем иметь 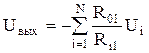 . Как видно из выражения выходное напряжение для такой схемы равно сумме произведений входных напряжений на коэффициент определяемый отношением сопротивления обратной связи и входным сопротивлением. Если выбрать все резисторы равными между собой, то все коэффициенты станут равными 1 и схема будет выполнять операцию суммирования. Если оставить один вход и коэффициент сделать равным 1, то получаем схему описываемую выражением Uвых = - Uвх. Получили схему, изменяющую знак входного напряжения – инвертор.
. Как видно из выражения выходное напряжение для такой схемы равно сумме произведений входных напряжений на коэффициент определяемый отношением сопротивления обратной связи и входным сопротивлением. Если выбрать все резисторы равными между собой, то все коэффициенты станут равными 1 и схема будет выполнять операцию суммирования. Если оставить один вход и коэффициент сделать равным 1, то получаем схему описываемую выражением Uвых = - Uвх. Получили схему, изменяющую знак входного напряжения – инвертор.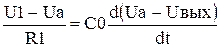 . В этом уравнении не определена переменная Ua. Для ее определения воспользуемся основным уравнением операционного усилителя
. В этом уравнении не определена переменная Ua. Для ее определения воспользуемся основным уравнением операционного усилителя 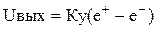 . В зтом выражении
. В зтом выражении 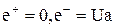 , и, следовательно, Ua = -Uвых/Ку. Выходное напряжение всегда величина конечная, не превышающая напряжение питания, а коэффициент усиления Ку величина большая в пределе стремящаяся к бесконечности, и, следовательно, будем иметь Ua = - Uвых/(Ку → ∞) = → 0. Выполняя подстановку и разрешая уравнение относительно выходного напряжения, получаем
, и, следовательно, Ua = -Uвых/Ку. Выходное напряжение всегда величина конечная, не превышающая напряжение питания, а коэффициент усиления Ку величина большая в пределе стремящаяся к бесконечности, и, следовательно, будем иметь Ua = - Uвых/(Ку → ∞) = → 0. Выполняя подстановку и разрешая уравнение относительно выходного напряжения, получаем 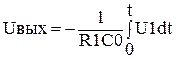 . Полученное уравнение показывает, что выходное напряжение интегратора равно интегралу от входного умноженного на постоянный коэффициент 1/(R1C0). Учитывая, что у интегратора можно организовать несколько входов и предварительно зарядить конденсатор обратной связи общее уравнение будет иметь вид
. Полученное уравнение показывает, что выходное напряжение интегратора равно интегралу от входного умноженного на постоянный коэффициент 1/(R1C0). Учитывая, что у интегратора можно организовать несколько входов и предварительно зарядить конденсатор обратной связи общее уравнение будет иметь вид 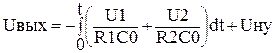 . Интегратор имеющий несколько входов называют – интегросумматор. Предварительный заряд конденсатора обратной связи используют для задания начальных условий.
. Интегратор имеющий несколько входов называют – интегросумматор. Предварительный заряд конденсатора обратной связи используют для задания начальных условий.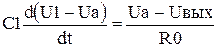 . Принимая допущения сделанные при выводе уравнения интегратора, и разрешая уравнение относительно выходного напряжения получаем уравнение описывающее дифференциатор.
. Принимая допущения сделанные при выводе уравнения интегратора, и разрешая уравнение относительно выходного напряжения получаем уравнение описывающее дифференциатор. 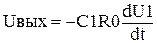 , уравнение показывает, что данная схема выполняет операцию дифференцирования входного напряжения. В связи с высокой чувствительностью дифференциатора к импульсным помехам применение его ограничено.
, уравнение показывает, что данная схема выполняет операцию дифференцирования входного напряжения. В связи с высокой чувствительностью дифференциатора к импульсным помехам применение его ограничено.
 Рассмотренные решающие элементы являются основными и позволяют решать с их использованием дифференциальные уравнения. Поэтому далее рассмотрим, как же можно решать дифференциальные уравнения. Для простоты понимания покажем это на примере.
Рассмотренные решающие элементы являются основными и позволяют решать с их использованием дифференциальные уравнения. Поэтому далее рассмотрим, как же можно решать дифференциальные уравнения. Для простоты понимания покажем это на примере.


