
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разновидности обратной связи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Существует несколько способов снятия сигнала обратной связи и передачи его во входную цепь усилителя. В соответствии с используемым способом называют вид обратной связи.
Обратная связь по току состоит в том, что сопротивление датчика Rд включено последовательно с сопротивлением нагрузки, и напряжение на нем пропорционально току нагрузки. Напряжение пропорциональное току нагрузки все или часть его подается на вход цепи обратной связи. Существует два вида подачи сигнала из цепи обратной связи во входную цепь. Схемы подачи сигналов на вход усилителя показаны на рис.74 и 75.
связи подается на вход усилителя последовательно входному усиливаемому сигналу. Таким образом, имеем возможность построения четырех разновидностей усилительных устройств с обратной связью.
Частотные свойства усилителей однозначно определяются амплитудно-частотной и фазово-частотной характеристиками.
Uвых(јω) = I(јω)*Xc, где I(јω) – ток в контуре, а Xc = 1/ јωС – сопротивление конденсатора. Найдя ток и выполнив подстановки, получим:
Разрешая это уравнение относительно передаточной функции, будем иметь.
- если ω << ωp, то отношение квадратов частот оказывается намного меньше 1, и с минимальной ошибкой можно считать │H(jω)│= 1, - если ω >> ωp, то единица под корнем намного меньше отношения квадратов частот, и можно считать │H(jω)│= ωp ⁄ω.
Как видно на графике при использовании аппроксимации обязательно получаем ошибку, но эта ошибка на частоте полюса и равна –3дБ. Эта функция построена для цепи с ωp = 100 1/сек. Так же на графике видно, что после перегиба график идет с наклоном –20 дБ/дек. Полную информацию об усилительном устройстве можно получить, если совместно с АЧХ рассматривать фазово-частотную характеристику (ФЧХ). Фазово-частотная характеристика выражается функциональной зависимостью φ(ω) = Σi (±arctg(ω/ωi)), где i -- номер частоты полюса или нуля, причем функция берется со знаком минус для полюса и плюс для нуля функции. Для RC цепи ФЧХ выражается зависимостью φ(ω) = - arctg(ω/ωp). График ФЧХ и его аппроксимация по Боде приведены на рис.78. на рисунке видно, что сама функция гладкая, на которой четко видна характерная точка – на частоте полюса сдвиг равен –45град. Аппроксимация Боде ФЧХ -- линейная ломаная кривая имеющая две точки перегиба: первая при 0,1ωp сдвиг ноль градусов, вторая при 10ωp сдвиг –90градусов. При частотах меньших 0,1ωp и больших 10ωp график ФЧХ расположен горизонтально. Точное совпадение аппроксимации и функции в точке ωp -- - 45град. Аппроксимация Боде вносит искажения в график и соответственно погрешность отображения, максимальная величина которой 5,7град.
В стандартной форме записи передаточная функция является дробью, в числителе и знаменатале которой произведения двучленов. Корни двучленов расположенных в числителе называют нулями, в знаменателе – полюсами. При построении аппроксимации Боде по виду передаточной функции нужно иметь в виду: - АЧХ на частоте нуля получает перегиб и далее идет с наклоном +20дБ/дек по отношению к предыдущему участку; - АЧХ на частоте полюса получает перегиб и далее идет с наклоном -20дБ/дек по отношению к предыдущему участку; - ФЧХ на частоте одной десятой частоты нуля получает перегиб и идет с наклоном +45град/дек до частоты равной десяти частотам нуля, после которой сдвиг составит +90 градусов и далее останется неизменным; - ФЧХ на частоте одной десятой частоты полюса получает перегиб и идет с наклоном -45град/дек до частоты равной десяти частотам полюса, после которой сдвиг составит -90 градусов и далее останется неизменным. Например, передаточная функция может иметь вид Рассмотрим построение АЧХ и ФЧХ для заданного примера. Выберем ω0 = 10 1/сек, ωp1 = 100 1/сек, ωp2 = 1000 1/сек, Ку = 100 – коэффициент усиления на постоянном токе. АЧХ в децибелах будем рассчитывать по формуле,
ФЧХ будем рассчитывать по формуле,
Рассчеты характеристик выполнены с помощью пакета MATCAD. На графиках характеристик также показаны аппроксимации Боде (АЧХ – рис. 79, ФЧХ – рис. 80).
На рисунке 79 показана АЧХ, заданная передаточной функцией. Тонкой плавной линией показана сама функция, а толстой ломаной линией показана ее аппроксимация Боде. Видно, что аппроксимация
имеет максимальные погрешности на частотах нулей и полюсов. На рисунке 80 показана сама функция а также построение ее аппроксимации Боде. Цифрами 1, 2, 3 обозначены графики фазовых сдвигов: 1 – сдвиг на частоте нуля, 2 и 3 – сдвиги на частотах полюсов. Для построения полной ФЧХ необходимо геометрически просуммировать сдвиги нулей и полюсов. Полная аппроксимация ФЧХ примера обозначена кружками. Совместный анализ АЧХ и ФЧХ дает возможность оценить устойчивость усилителя. Лекция 11
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.011 с.) |


 Рассмотрим способы снятия сигнала с выхода усилителя
Рассмотрим способы снятия сигнала с выхода усилителя Обратная связь по напряжению показана на рис. 72, а обратная связь по току показана на рис. 73.
Обратная связь по напряжению показана на рис. 72, а обратная связь по току показана на рис. 73. Обратная связь по напряжению состоит в том, что сопротивление датчика Rд включено на выходное напряжение, т.е. параллельно сопротивлению нагрузки. В зависимости от положения движка потенциометра все напряжение или часть его подается на вход цепи обратной связи.
Обратная связь по напряжению состоит в том, что сопротивление датчика Rд включено на выходное напряжение, т.е. параллельно сопротивлению нагрузки. В зависимости от положения движка потенциометра все напряжение или часть его подается на вход цепи обратной связи.
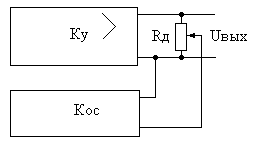
 Параллельная обратная связь состоит в том, что сигнал с выхода цепи обратной связи подается на вход усилителя параллельно входному усиливаемому сигналу.
Параллельная обратная связь состоит в том, что сигнал с выхода цепи обратной связи подается на вход усилителя параллельно входному усиливаемому сигналу. Последовательная обратная связь состоит в том, что сигнал с выхода цепи обратной
Последовательная обратная связь состоит в том, что сигнал с выхода цепи обратной 2.4. Частотные свойства усилителей.
2.4. Частотные свойства усилителей.
 Амплитудно-частотная характеристика (АЧХ) определяется в частотной области и представляет собой зависимость H(jω) = Uвых(jω)/Uвх(jω), причем H(0) = Ку. Рассмотрим особенности определения АЧХ на простейшем примере передаточной функции RC цепи, схема которой показана на рис. 76. Цепь состоит из резистора и конденсатора, включенных последовательно, и подключенных к источнику сигнала Uвх. Выходное напряжение снимаем с конденсатора.
Амплитудно-частотная характеристика (АЧХ) определяется в частотной области и представляет собой зависимость H(jω) = Uвых(jω)/Uвх(jω), причем H(0) = Ку. Рассмотрим особенности определения АЧХ на простейшем примере передаточной функции RC цепи, схема которой показана на рис. 76. Цепь состоит из резистора и конденсатора, включенных последовательно, и подключенных к источнику сигнала Uвх. Выходное напряжение снимаем с конденсатора. .
. . В этом выражении вводят обозначение RC = τ =1/ωp. Константа ωp называется полюсом на оси частот, и на этой частоте график АЧХ получает перегиб и далее идет с наклоном -20 дБ/дек. График АЧХ строится в осях: горизонтальная ось – частота или отношение частот в логарифмическом масштабе, вертикальная – Н[дБ]. Децибелы определяют выражением H[дБ] = 20*log10(│H(jω)│), т.е. двадцать логарифмов по основанию десять модуля передаточной функции.
. В этом выражении вводят обозначение RC = τ =1/ωp. Константа ωp называется полюсом на оси частот, и на этой частоте график АЧХ получает перегиб и далее идет с наклоном -20 дБ/дек. График АЧХ строится в осях: горизонтальная ось – частота или отношение частот в логарифмическом масштабе, вертикальная – Н[дБ]. Децибелы определяют выражением H[дБ] = 20*log10(│H(jω)│), т.е. двадцать логарифмов по основанию десять модуля передаточной функции.
 Алгебраическая форма представления передаточной функции RC цепи имеет вид
Алгебраическая форма представления передаточной функции RC цепи имеет вид  , а показательная форма представления имеет вид
, а показательная форма представления имеет вид  , где φ – аргумент передаточной функции, показывающий фазовый сдвиг между входным и выходным сигналами. Модуль функции, определяющий АЧХ, находится по формуле
, где φ – аргумент передаточной функции, показывающий фазовый сдвиг между входным и выходным сигналами. Модуль функции, определяющий АЧХ, находится по формуле  . По виду формулы можно сделать вывод о том, что вид графика должен быть гладким и непрерывным. Проанализируем модуль функции с целью упрощения построения графика:
. По виду формулы можно сделать вывод о том, что вид графика должен быть гладким и непрерывным. Проанализируем модуль функции с целью упрощения построения графика:
 На основе анализа приходим к выводу, что при низких частотах (меньших частоты полюса) график АЧХ будет расположен горизонтально при значении H[дБ] =0, так как log10 (1) = 0. На частоте полюса график функции получает перегиб и далее идет с наклоном -20 дБ/дек, относительно предыдущего участка. Это определяется тем, что log10 (0,1) = -1 (отношение частот равное 10 или 0,1). Такой подход к построению графиков разработан французом Боде, и поэтому график АЧХ, построенный таким образом, называют аппроксимация Боде АЧХ. На рис. 77 приведена сама функция АЧХ и ее аппроксимация, тонкая линия – функция, толстая линия – аппроксимация функции.
На основе анализа приходим к выводу, что при низких частотах (меньших частоты полюса) график АЧХ будет расположен горизонтально при значении H[дБ] =0, так как log10 (1) = 0. На частоте полюса график функции получает перегиб и далее идет с наклоном -20 дБ/дек, относительно предыдущего участка. Это определяется тем, что log10 (0,1) = -1 (отношение частот равное 10 или 0,1). Такой подход к построению графиков разработан французом Боде, и поэтому график АЧХ, построенный таким образом, называют аппроксимация Боде АЧХ. На рис. 77 приведена сама функция АЧХ и ее аппроксимация, тонкая линия – функция, толстая линия – аппроксимация функции.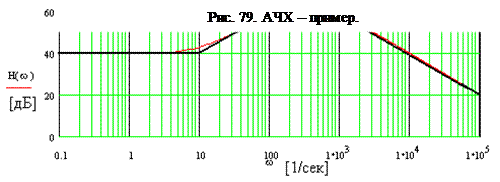
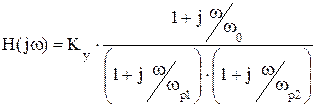 . По уравнению видно, что данная функция имеет один ноль с частотой – ω0 и два полюса с частотами – ωp1, ωp2.
. По уравнению видно, что данная функция имеет один ноль с частотой – ω0 и два полюса с частотами – ωp1, ωp2.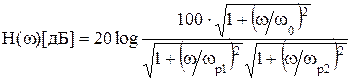 .
.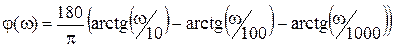 .
.




