
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости в пространстве.Содержание книги Поиск на нашем сайте
Задача. Построить уравнение плоскости по точке (2,2,8) и перпендикуляру (3,3,7). Ответ. Задача. Построить уравнение плоскости по точке Ответ. Задача. Построить уравнение плоскости, проходящей через (0,0,0) параллельно 2 направляющим (1,1,2) и (2,1,3). Ответ.
Задача. Построить уравнение плоскости по трём точкам. А(1,2,3), В(3,5,7), С(4,5,6). Ответ.
Задача. Найти расстояние от точки M0 (1,3,5) до плоскости Задача. Найти расстояние от точки M0 (7,15,22) до плоскости Задача. Даны точки Вывести уравнение прямой, содержащей А1В1, и найти расстояние от точки С1 до этой прямой (то есть высоту треугольника). Ответ. Прямая Задача 3. Найти угол между двумя плоскостями: Прямая в пространстве Задача. Построить уравнение прямой в пространстве (каноническое, параметрическое) по точке Ответ. Задача. Построить уравнение прямой, лежащей в пересечении двух плоскостей Ответ. Задача. Доказать, что прямая Ответ. (0,0,1). Задача. Найти угол между прямой и плоскостью Задача. Найти параметрические и канонические уравнения прямой, перпендикулярной к плоскости треугольника с вершинами Ответ. Канонические параметрические
Задача. Доказать, что две прямые в пространстве
Ответ. точка пересечения (1,1,2). Задача 11. Доказать, что две прямые в пространстве:
Задача. Доказать, что прямые Задача. Вычислить расстояние от точки (4,4,-2) до прямой Задача. Даны три точки А(1,1,1),В(2,2,3),С(2,1,2). Вывести уравнение прямой, содержащей АВ, и найти расстояние от точки С до этой прямой (высота треугольника АВС). Ответ. Задача. Найти точку пересечения плоскости Задача. Через точку Задача. Заданы 2 прямые в пространстве, одна - своими параметрическими уравнениями, а другая как пересечение пары плоскостей:
Доказать, что эти прямые параллельны, и найти уравнение плоскости, содержащей их. Ответ. Плоскость Задача. Доказать, что кривая является эллипсом, найти каноническое уравнение, центр и полуоси. Ответ. Центр Задача. Доказать, что кривая является эллипсом, найти каноническое уравнение, центр и полуоси, построить чертёж. Ответ. Центр Задача. Доказать, что однополостный гиперболоид Задача. Доказать, что кривая Ответ. Центр (3,-1), полуоси 3 и
«Введение в математический анализ. Множества и функции» Задача. Точка движется по окружности единичного радиуса вокруг начала координат в плоскости. Температура распределена по закону:
Ответ. Температура в зависимости от времени для этой точки изменяется так:
Задача. Найти область определения функции:
Задача. Найти область определения функции:
Ответ. Кольцо Задача. Найти область определения функции 3 переменных:
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.12 (0.011 с.) |

 .
. и двум направляющим векторам
и двум направляющим векторам  (4,2,3) и
(4,2,3) и  .
. .
. .
. .
. .
. .
. ,
,  ,
,  .
. , расстояние 3.
, расстояние 3. и
и  . Ответ.
. Ответ.  .
. и направляющему
и направляющему 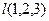 .
. ,
, 
 и
и  .
. ,
,  .
. пересекает ось
пересекает ось  и найти точку пересечения.
и найти точку пересечения.
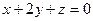 . Ответ.
. Ответ.  .
. ,
,  ,
,  и проходящей через вершину А.
и проходящей через вершину А. ,
, .
. и
и  пересекаются, и найти точку пересечения.
пересекаются, и найти точку пересечения. и
и  скрещивающиеся, и найти расстояние между ними. Ответ.
скрещивающиеся, и найти расстояние между ними. Ответ.  .
. и
и  пересекаются и найти точку. Ответ. (3,7,-6).
пересекаются и найти точку. Ответ. (3,7,-6). в пространстве. Ответ.
в пространстве. Ответ.  .
. .
. и прямой
и прямой  . Ответ. Точка пересечения
. Ответ. Точка пересечения  .
. и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти косинус тупого угла между этими плоскостями. Ответ.
и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти косинус тупого угла между этими плоскостями. Ответ. 
 и
и  .
.
 , полуоси
, полуоси  и
и  .
.
 , полуоси 1 и 3.
, полуоси 1 и 3. содержит прямолинейные образующие.
содержит прямолинейные образующие. является эллипсом, найти каноническое уравнение, центр и полуоси.
является эллипсом, найти каноническое уравнение, центр и полуоси. . Найти для этой точки функцию, как меняется температура в зависимости от времени.
. Найти для этой точки функцию, как меняется температура в зависимости от времени. .
. . Ответ.
. Ответ.  .
. .
. .
. . Ответ. Шар радиуса 1:
. Ответ. Шар радиуса 1:  .
.


