Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Магнитное поле постоянного токаСодержание книги Поиск на нашем сайте Основные формулы и указания к решению задачи Связь магнитной индукции
где m – магнитная проницаемость изотропной среды; m0 – магнитная постоянная. В вакууме m = 1, и тогда выражение (4.1) примет вид:
Закон Био-Савара-Лапласа
где
a – угол между радиусом-вектором и направлением тока в элементе провода. Магнитная индукция в центре кругового тока определяется по формуле:
где R – радиус кругового витка. Магнитная индукция на оси кругового тока определяется по формуле:
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция. Магнитная индукция поля прямого тока определяется по формуле:
где r 0 – расстояние от оси провода до точки, в которой определяется магнитная индукция. Магнитная индукция поля, создаваемого отрезком провода с током (рис. 4.1) определяется по формуле:
Рис. 4.1. Отрезок провода с током
Направление вектора магнитной индукции При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция – cos a2 = cos a1 = cos a, тогда
Магнитная индукция поля соленоида определяется по формуле: B = mm0 nI, (4.9) где n – отношение числа витков соленоида к его длине.
Пример решения задачи Бесконечно длинный провод изогнут так, как это изображено на рис. 4.2а. Радиус R дуги окружности равен 10 см. Определить магнитную индукцию В поля, создаваемого в точке О током I = 80 A, текущим по этому проводу. Решение. Магнитную индукцию
где
а б Рис. 4.2. Проводник с током
Так как точка О лежит на оси провода 1, то В 1 = 0 и тогда
Учитывая, что векторы B = B 2 + B 3. (4.12) Магнитную индукцию B 2 найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока:
В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому
Магнитную индукцию В 3 найдем, воспользовавшись соотношением:
В нашем случае r 0 = R, a1 = p/2 (сos a1 = 0), a2 ® p (сos a2 = –1). Тогда
Используя найденные выражения для В 2 и В 3, получим
Выполним проверку единиц измерения величин.
Произведем вычисления:
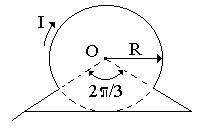
4.3 Задание для самостоятельного выполнения по вариантам Бесконечно длинный тонкий проводник с током I = 100 А изогнут так, как показано на рис. 4.3. Радиус изгиба R = 10 см. Определить в точке О магнитную индукцию поля В, создаваемого этим током. Направление тока показано на рисунке стрелкой.
Рис. 4.3. Формы проводников с током
Продолжение рис. 4.3. Формы проводников с током
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

 с напряженностью
с напряженностью  магнитного поля определяется следующим выражением:
магнитного поля определяется следующим выражением: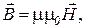 (4.1)
(4.1) (4.2)
(4.2) или
или 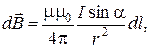 (4.3)
(4.3) – магнитная индукция поля, создаваемого элементом провода длиной dl с током I;
– магнитная индукция поля, создаваемого элементом провода длиной dl с током I;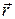 – радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;
– радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; , (4.4)
, (4.4)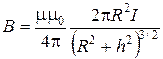 , (4.5)
, (4.5) , (4.6)
, (4.6) (4.7)
(4.7)
 (4.8)
(4.8)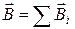 . В нашем случае провод можно разбить на три части (рис. 4.2б): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
. В нашем случае провод можно разбить на три части (рис. 4.2б): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда , (4.10)
, (4.10) ,
, 
 – магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.
– магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.
 (4.11)
(4.11) и
и  . (4.13)
. (4.13) . (4.14)
. (4.14) . (4.15)
. (4.15) . (4.16)
. (4.16) или
или  (4.17)
(4.17) (4.18)
(4.18) Тл.
Тл.