
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Робота 8. Дослідження фазового портрета нелінійної системи з релейним регуляторомСодержание книги
Поиск на нашем сайте Мета роботи Вивчити методику розрахунку і побудови фазового портрета нелінійної системи другого порядку, за допомогою осцилографа дослідити фазовий портрет нелінійної системи Теоретичний аналіз На рис. 8.1 приведена структурна схема нелінійної системи другого порядку
Відповідно до структурної схеми диференціальне рівняння, що описує динамічні властивості системи має вигляд
Рівняння /1/ - нелінійне із-за нелінійиості статичної характеристики нелінійного елемента и(є). Характер нелінійиості такий, що апроксимується відрізками прямих згідно з рівняннями
де Таким чином рух системи можна представити двома лінійними рівняннями, які описують певні ділянки траєкторії у відповідності до умов / 2/ і /З/
Для побудови фазового портрета рівняння /4/ /5/ записують у формі Коші. Так, для рівняння /4/ отримують систему рівнянь
Робота 2. Дослідження перехідних характеристик типових ланок Мета роботи Експериментальне дослідження перехідних характеристик типових ланок систем автоматичного керування та визначення параметрів ланок за їх перехідним характеристиками Теоретичні відомості Для розрахунку систем автоматичного керування технологічними процесам чи промисловими об'єктами необхідно знати математичну модель об'єкта керування, керуючого пристрою та інших елементів системи, які прийнято називають ланками системи. Математичний опис (математична модель ланки) складається; диференціальних та алгебраїчних рівнянь, що встановлюють зв'язок між вхідним* вихідними сигналами. При цьому алгебраїчні рівняння описують усталений стан системи або окремої ланки, коли всі похідні від вхідних і вихідних сигналів рів нулю. Ці рівняння називають рівняннями статики. Диференціальні рівняння характеризують поведінку системи у часі і називають* рівняннями динаміки. Для отримання динамічних характеристик застосовують різ аналітичні та експериментальні методи. Аналітичні методи ґрунтується на закон; фізики, хімії, електротехніки та інших. В найпростішому випадку, при зосередженості параметрів ланок, стаціонарно їх динамічних властивостей у часі та лінійності при малих змінах вхідних д динамічні властивості ланки (системи) описуються лінійними диференціальний, рівняннями з постійними коефіцієнтами
де x і у - відповідно вхідна і вихідна величини, а і Ь - коефіцієнти. Для опису властивостей ланок більш зручно користуватися не диференціальна рівняннями, а перерахованими нижче функціями і характеристиками, а безпосередньо випливають з диференціального рівняння: передаточною функцією W(p); перехідною характеристикою h(t); частотними характеристиками W(jω). Для визначення передаточної і перехідної функцій ланки найбільше доцільно використовувати перетворення Лапласа, що ґрунтується на формулах прямо перетворення Лапласа:
і зворотного перетворення Лапласа:
Тут під s мається на увазі комплексна змінна s = перетворення Лапласа переходить в його окремий випадок - перетворення Фур'є. Передаточною функцією лінійної ланки називається відношення зображення Лапласа вихідної величини Y(s)до зображення вхідної величини Х(s)при нульових початкових умовах:
В операторній формі диференціальне рівняння приймає вигляд:
З виразу для передаточної функції видно, що вона є відношенням двох поліномів по 5 з коефіцієнтами, що відповідають коефіцієнтам диференціального рівняння. Таким чином встановлюється однозначний зв'язок між передаточною функцією та диференціальним рівнянням. Перехідною характеристикою ланки (системи) називають її реакцію на одиничну ступінчасту дію. Вона показує, як змінюється вихідна величина ланки, коли вхідна величина є одиничною ступінчастою функцією. Математично одинична ступінчаста функція задається виразом:
Зображення Лапласа одиничної ступінчастої функції:
Тому зображення перехідної характеристики:
Переходячи від зображення до оригіналу, знаходимо вираз для перехідної характеристики:
Цей вираз підкреслює наявність зв'язку між перехідною характеристикою і передаточною функцією ланки. Таким чином за перехідною характеристикою системи можна оцінити її динамічні властивості. У випадку, коли перехідну характеристику визначено експериментальним шляхом на її основі можуть бути встановлені параметри ланки. Разом з тим, знаючи реакцію лінійної системи на ступінчасту дію, можна розрахувати реакцію на довільну дію, використовуючи інтеграл згортки:
7.5. Контрольні запитання 1.Поясніть роботу системи за принциповою схемою. 2. Поясніть роботу релейного регулятора. 3. Яка послідовність спадання математичної моделі нелінійної системи 4. У чому полягає суть методу припасовування? 5. Яка особливість усталеного режиму досліджуваної системи. 6. Від чого залежить похідна регулювання в досліджуваній системі?
6. Порівняти результати моделювання з даними теоретичного аналізу.
Рис. 4. Схема дослідження Порядок виконання роботи 1. Завантажте програму СІАМ. 2. Складіть структурну схему системи з типових блоків, згідно рис. 4. Задайте значення параметрів блоків відповідно: а) для генератора ступінчатого сигналу (блок 1) k = 1; б) для релейного регулятора (блок 3); xl= -0.1; х2=0.1; у0=1; в) для об'єкта (блок 4) к = 0.01 3. Для дослідження процесів в нелінійній системі за допомогою функціональної клавіші Р7-Мод перейдіть в режим моделювання. Далі функціональною клавішею F2-Мет відкрийте підменю методи інтегрування і виберіть метод чисельного інтегрування Фельберга та задайте: - похибку, не більше 0,001; - початковий час розрахунку t()=0 c; - кінцевий час розрахунку tк=200 с. 4. Функціональною клавішею F3-C4eT проведіть розрахунок роботи релейного регулятора та перехідного процесу. Дані роботи релейного регулятора занесіть табл. 1 Таблиця 1
Результати розрахунку перехідної характеристики занесіть в табл. 2,
7. За результатами моделювання побудуйте часову діаграму роботи релейного регулятора та перехідну характеристику системи. Зробіть висновок про відповідність теоретичних і експериментальних даних.
В роботі досліджуються перехідні характеристики типових ланок: пропорційної - інтегруючої - диференціюючої - аперіодичної - коливної - Програма роботи 1. Зібрати схему дослідження пропорційної, інтегруючої і диференціюююч ланок. Задаючи параметри ланок згідно з варіантом, почергово провести моделювання перехідних процесів цих ланок 2. Зібрати схему дослідження аперіодичної та коливної ланок. Задаю* параметри ланок згідно з варіантом почергово провести моделювання перехідна процесів для інерційної та коливної ланок. 3. За даними експериментів побудувати перехідні характеристик досліджуваних ланок, 4. З графіків перехідних характеристик ланок знайти їх параметри ■ порівняти з заданими. Варіанти рекомендованих параметрів ланок зведено в табл. І. Таблиця 1
2.4, Порядок виконання роботи 1. Завантажте комп'ютерну програму SIAM. Далі з основного меи програми функціональною клавішею F2 переведіть програму у режим введені моделі системи. Першим блоком виберіть генератор ступінчастого сигналу зображенням одиничної стулінчатої функції. В діалоговому вікні для генератора задайте к=1. Подібним чином наступним блоком виберіть пропорційну ланку, яка має позначення К. Проведіть моделювання перехідного процесу. Дані занесіть в табл. 2. Пропорційна ланка, Кп=...
Таб лиця 2
2. Для дослідження інтегруючої ланки за допомогою клавіші F4 видаліть пропорційну ланку. Далі функціональною клавішею F2 переведіть програму у режим введення моделі системи та виберіть наступну ланку дослідження -інтегруючу. Задайте коефіцієнт передачі інтегруючої ланки згідно з варіантом і проведіть моделювання перехідного процесу. Дані занесіть у табл. 3. Інтегруюча ланка, Kt=...
Таблиця З
3. Для дослідження диференціюючої ланки знову видаліть інтегруючу ланку. Виберіть наступну ланку дослідження - диференціюючу. Задайте коефіцієнт передачі диференціюючої ланки згідно з варіантом і проведіть моделювання перехідного процесу. Дані занесіть у табл. 4. Диференціююча ланка,
Т аблиця 4
4. Для дослідження аперіодичної ланки замініть диференціюючу ланку на аперіодичну. Задайте коефіцієнт передачі аперіодичної ланки згідно з варіантом і проведіть моделювання перехідного процесу, дані занесіть у табл. 5. Аперіодична ланка, К0=...; Т =.... с.
Т аблиця 5
5. Для дослідження властивостей коливної ланки введіть відповідний блок та задайте відповідні параметри згідно з варіантом та проведіть моделювання перехідного процесу. Дані занесіть у табл. 6. Коливна ланка, К0=...; T=... с; Y0=....
Таблиця 6
рівняння може бути представлено у вигляді двох лінійних рівнянь, які відповідають включеному (1) і виключеному (2) станові реле
Розв'язок цих рівнянь дає змогу знаходити зміну регульованої величини у часі на окремих інтервалах часу, котрі відповідають різним станам реле. При цьому використовується метод "припасовування" або "зшивання" при якому кінцеві значення зміни регульованої величини на попередньому інтервалі приймаються за початкові для розрахунку руху на наступному інтервалі. При к = 0.01
де
Після першого вимикання реле рівень рідини буде знижуватися. Закон змії рівня на другому інтервалі знайдемо з розв'язку рівняння
Згідно з принципом припасовування початкові умови для другого інтервш відповідають кінцевим значенням на першому інтервалі, тобто
У результаті зміна рівня на другому інтервалі
Другий інтервал закінчиться, коли рівень знизиться до відмітки 0.9 м, тобто момент
Далі побудову можна продовжувати аналогічним чином. Програма роботи 1. Скласти схему моделювання нелінійної системи. 2. Задати параметри і провести моделювання перехідного процесу. 3. Побудувати часову діаграму роботи реле. 4. Побудувати перехідну характеристику нелінійної системи. 5. Визначити амплітуду і частоту автоколивань.
Рис. 2. Статична характеристика регулятора та її математичний опис. На рис. 3. наведена структурна схема системи регулювання.
Рис. 3. Структурна схема системи. Зі структурної" схеми видно, що зображення регульованої величини Н(р) зв'язано ззображенням регулюючої дії Δ Q(p) через передаточну функцію лінійної частини нелінійної системи:
Звідси диференціальне рівняння об'єкта у операторній формі
Відповідно рівняння для оригіналів
Величина
є також нелінійним. Як слідує з рис.2. характер не лінійності є такий, що по того у якому стані знаходиться реле. Таким чином нелінійне
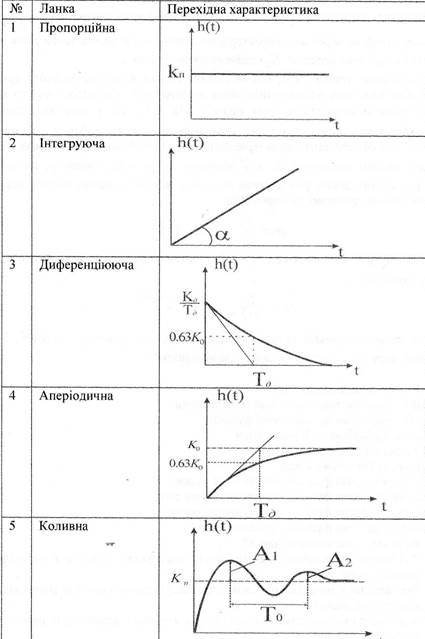
4. При побудові графіків перехідних характеристик користуйтеся прав оформлення графічної документації, прийнятими у науковій літературі. 5. Методику знаходження параметрів ланок з графіків пере? характеристик ілюструє табл. 7. Таблиця 7
Як видно з табл. 7 визначення коефіцієнта передачі пропорційної ланки труднощів не викликає. Коефіцієнт передачі інтегруючої ланки визначається тангенсом кута нахилу прямої перехідного процесу. Слід розрізняти передаточні функції диференціюючої ідеальної та реальної ланок. Насправді для реальної ланки передаточна функція має вигляд: Тому з графіка перехідної характеристики спочатку визначають постійну часу Г,), а потім коефіцієнт передачі Кд диференціюючої ланки. Коефіцієнт передачі аперіодичної ланки рівний значенню до якого прямує усталене. Постійна часу аперіодичної ланки визначається інтервалом часу за який значення вихідної величини досягає рівня 0,63Ко. Постійну часу аперіодичної ланки можна також визначити через початкову швидкість, тобто з допомогою похідної до кривої перехідної характеристики в початковий момент (див. табл. 7). Щоб знайти параметри експериментальних даних розрахувати значення дійсної і уявної частин коренів характеристичного рівняння за формулами
Далі отримані значення а і параметрами ланки:
Розв'язавши отриману систему рівнянь, знаходять параметри ланки 2.5. Контрольні запитання 1. Дайте означення математичної моделі ланки. 2. Дайте означення передаточної функції. 3. Що таке рівняння динаміки ланки? 4. Що таке рівняння статики ланки? 5. Перерахуйте типові ланки. 6. Яка передаточна функція інтегруючої ланки? 7. Яка передаточна функція диференціюючої ланки? 8. Яка передаточна функція аперіодичної ланки? 9. Яка передаточна функція коливної ланки? 10. Як реалізована коливна ланка? 11. Яка методика знаходження параметрів інтегруючої ланки за її перехідною характеристикою? 12. Яка методика знаходження параметрів аперіодичної ланки за її перехідною характеристи кою? 13. Яка методика знаходження параметрів коливної ланки за її перехідною характеристикою?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 Рис. 8.1. Структурна схема системи
Рис. 8.1. Структурна схема системи
 - В при
- В при  >С,
>С, 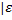 | < С,
| < С,  < с,
< с,  /4/
/4/ /5/
/5/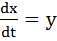 /6/
/6/


 + jω. При
+ jω. При 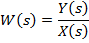
 Знайшовши відношення зображень, отримуємо вираз для передаточної функції:
Знайшовши відношення зображень, отримуємо вираз для передаточної функції:

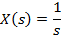




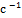 .
.

 ;
;
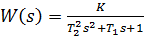
 =... с
=... с

 після включення релейного регулятора рівень рідини буде змінюватися за законом
після включення релейного регулятора рівень рідини буде змінюватися за законом
 -константа інтегрування, що визначається з початкових умов, у даному випадку початкові умови нульові Н(0) = 0, тому
-константа інтегрування, що визначається з початкових умов, у даному випадку початкові умови нульові Н(0) = 0, тому 
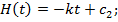

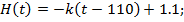
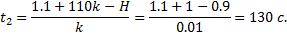





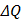 є нелінійною функцією
є нелінійною функцією 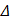 Н, а отже, диференціальне рівняння
Н, а отже, диференціальне рівняння

 і Тг коливної ланки слід, спочатку, на основі
і Тг коливної ланки слід, спочатку, на основі

 слід підставити у вирази, що зв'язують їх з
слід підставити у вирази, що зв'язують їх з




