
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичний аналіз якості регулюванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Зображення за Лапласом динамічної помилки системи знаходять за формулою:
При одноступінчатому вхідному сигналі зображення вхідної величини
Передаточна функція розімкнутої системи дорівнює добутку передаточні функцій регулятора і об'єкта: W(s)= Для І-регулятора:
s В роботі досліджується система з передаточною функцією об'єкта керування: Отже передаточна функція замкнутої системи:
Таким чином зображення за Лапласом динамічної помилки системи з регулятором:
За методом Мак-Лена квадратична інтегральна оцінка для системи третьої: порядку знаходиться за формулою:
Робота 6. Дослідження якості лінійної системи автоматичного керування Мета роботи Теоретичний розрахунок та експериментальне дослідження впливу коефіцієнтів передачі регуляторів на якість регулювання в лінійній системі на основі квадратичної інтегральної оцінки якості регулювання. Загальні відомості Для повноцінного функціонування система автоматичного керування повинна бути не тільки стійка, але й відповідати вимогам якості. Під якістю регулювання розуміють набір показників, які характеризують динаміку перехідного процесу і точність в усталеному режимі. Найпоширенішим способом оцінки якості є спосіб оцінки за перехідними характеристиками системи. Показники якості регулювання, що визначені за перехідними характеристиками називають прямими показниками якості. Крім того існують непрямі показники якості. До них зокрема належать кореневі критерії якості, інтегральні і частотні критерії якості. Серед прямих критеріїв якості виділяють такі: перерегулювання, час регулювання, коливальність та усталеному помилку (похибку). Перерегулюванням називають максимальне відхилення регульованої величини від її усталеного значення:
Часом регулювання називають проміжок часу від початку перехідного процесу до моменту, коли регульована величина відрізняється від усталеного значення на величину наперед заданої помилки, яка складає, як правило, 5% від усталеного значення. Відношення амплітуди коливань через період під час перехідного процесу називають коливальністю:
На практиці коливальність визначається числом повних коливань п визначених на протязі часу регулювання.
Інтегральні оцінки якості дають загальну оцінку швидкості затухання і відхилення регульованої величини за час регулювання. вони діляться на лінійні і квадратичні. Найпростіша квадратична оцінка є функціоналом від динамічної помилки системи і визначається формулою:
о дд - динамічна помилка системи. Динамічну помилка системи є відхиленням регульованої величини від усталеного значення
Робота 4. Дослідження стійкості лінійної системи автоматичного регулювання типовими регуляторами Мета роботи
Ознайомитися з методами аналізу стійкості лінійних систем з тиловим регуляторами та визначення критичних параметрів системи, дослідити вплив настроювальних параметрів регуляторів на стійкість системи Загальні відомості Під стійкістю систем автоматичного керування розуміють їх здатність повертатися до вихідного усталеного режиму після короткочасної дії керуючої і збурюючої величини, яка виводить систему з початкової рівноваги, Динамічні властивості лінійних систем описуються неоднорідний диференційними рівняннями з постійними коефіцієнтами. Ці рівняння прийнято записувати у вигляді
де у— регульована величина, X- вхідна дія. Ліва частина диференціального рівняння описує вільний рух системи
Цей рух стійкий, якщо
де упер - загальний розв'язок однорідного диференціального рівняння. Розв'язок однорідного диференціального рівняння /5.2/ знаходять у формі
де С, - сталі інтегрування, st- корені характеристичного рівняння системи. Характеристичне рівняння складається на основі диференціального рівнянні системи. Разом з тим характеристичне рівняння є рівнянням для полюс передаточної функції і може бути отримане з передаточної функції замкнутої системи, якщо знаменник передаточної функції прирівняти до нуля. Для рівняння /5.1/ воно матиме вид
Корені характеристичного рівняння можуть бути дійсними або комплексний числами. Для довільних пари комплексних коренів можна записати
Де Для стійкості лінійних систем необхідно і достатньо, щоб корені характеристичного рівняння були від'ємними і комплексними числами від'ємними, дійсними частини. Загальну умову стійкості можна сформулювати інакше: система є стійкою коли корені характеристичного рівняння лежать в лівій півплощині комплексної площини коренів (рис, 4.1). Таким чином, уявна вісь є межею, яка ділить комплексну площину коренів на дві області - ліву стійку і праву - нестійку. Система знаходиться на межі стійкості, якщо один з коренів попадає на уявну вісь. При цьому в системі виникають автоколивання. В такому режимі лінійна система експлуатуватися не може.
Рис. 4.1. Аналіз стійкості за коренями характеристичного рівняння: а) -система стійка, б) -система нестійка Існують методи, що дозволяють досліджувати стійкість систем автоматичного керування без знаходження коренів характеристичного рівняння. Вони мають назву критеріїв стійкості. Критерії стійкості поділяються на алгебраїчні і частотні. До алгебраїчних належать критерії Рауса, Гурвіца, Льєнара-Шіпара, до частотних -критерії Михайлова та Найквіста. Найчастіше для аналізу стійкості систем невисокого порядку (п S 5) та систем, до складу яких не входять особливі ланки, використовують критерій Гурвіца, який приводить до тієї ж самої системи нерівностей, що і критерій Рауса. Тому, інколи, ці критерії називають критеріями Рауса-Гурвіца. Для аналізу стійкості системи за критерієм Гурвіца складають визначник з коефіцієнтів характеристичного рівняння таким чином, що по головній діагоналі розташовують коефіцієнти від ап_} до ап, далі місця в стовпцях над діагоналлю заповнюють коефіцієнтами в порядку зростання індексів, а знизу від діагоналі - із меншими індексами. Пусті місця заповнюють нулями. За допомогою функціональної клавіші Р4-Ред відкрийте для редагування діалогове вікно ланки постійного запізнення та змініть постійну часу і
Аналогічним чином промоделюйте перехідний процес в досліджуваній системі при
Повторіть розрахунок, а дані занесіть в табл. 3.
Висновки по роботі За даними таблиць побудуйте перехідні характеристики системи при задані величинах постійного запізнення. Проаналізуйте графіки перехідних характерне!'! та зробіть висновок про вплив величини постійного запізнення на характер перехідного процесу. 5.7. Контрольні запитання 1. Запишіть вираз для передаточної функції ланки з постійним запізненням. 2. Якими диференціальними рівняннями описується динаміка ланки постійним запізненням? 3. Як визначаються запаси стійкості систем автоматичного керування? 4. Який вплив величини запізнення на запаси стійкості системи? 5. Як величини запасу стійкості проявляються в характері перехідні процесів? 6. Яка система автоматичного керування з постійним запізненням називаєш граничною? 7. Яке значення постійного запізнення називається критичним? Яка методика визначення величини критичного запізнення?
Програма роботи 1. Скласти схему моделювання процесів в системі автоматичного керування з постійним запізненням. 2, Дослідити вплив постійного запізнення стійкість лінійної системи автоматичного регулювання. Схема дослідження
Робота виконується за допомогою ЕОМ з використанням програми автоматичного моделювання і параметричної оптимізації STAM. Досліджувана система складається з І-регулятора і об'єкта регулювання, /динамічні властивості якого можна представити інерційною ланкою першого порядку з постійним запізненням (рис. 3).
Рис. 3. Схема моделювання процесів в системі автоматичного регулювання з постійним запізненням Порядок виконання роботи 1. Завантажте комп'ютерну програму STAM. В режимі набору моделі з типових блоків складіть схему моделювання згідно з рис. 3. Задайте наступні значення параметрів блоків: а) для генератора ступінчастого сигналу (блок 1) - k = 1; б) для регулятора (блок 3) - к = 4; в) для об'єкта (блок 4) - к - 1 і Т = 1 с; г) для ланки із запізненням (блок 5) - к - 1 і Т = 0,01. с. 2. Для дослідження впливу величини запізнення на стійкість системи перейдіть в режим моделювання (функціональна клавіша Fl-Мод). За допомогою функціональної клавіші F2-MeT відкрийте діалогове вікно методів інтегрування і встановіть метод чисельного інтегрування - Фельберга та задайте: похибку, не більше 0,001; початковий час розрахунку 10=0 с; кінцевий час розрахунку ік~5 с. Розрахунок перехідної характеристики починається з натискання клавіші F3. Результати розрахунку можуть бути виведені на екран монітора в графічній формі або у вигляді таблиць. Дані розрахунку при
За критерієм Гурвіца замкнута система стійка, якщо при додатному знаї коефіцієнта ап, є також додатними, головний визначник Гурвіца Δ і всі йоі діагональні мінори - М1, М2,..-, Мn_j. Діагональні мінори утворюють з головного визначника шляхом викреслювані відповідного числа рядків і стовпців. Застосування критерію стійкості Гурвіца до систем першого і другого порядк показує, що вони є стійкими при додатних параметрах системи, однак систєк-третього і вищого порядків можуть втратити стійкість і при додатних значенні параметрів. Частотні критерії стійкості є досить зручними: для аналізу стійкості систе високого порядку та систем із постійним запізненням. При аналізі систем автоматичного керування важливо встановити вплив окремі параметрів системи на її стійкість та визначити область допустимих значеі параметрів. Для цього можуть бути використані розглянуті вище критерії стійкос метод D-розбиття. Зокрема для знаходження критичного значення варійованого коефіцієнт передачі Ккр чи однієї з постійних часу Ткр, при яких система буде знаходитись і
межі області стійкості, можна скористатися критерієм стійкості Гурвіца. Для цьої необхідно прирівняти до нуля головний визначник відповідні мінори визначиш Гурвіца та розв'язати отримані рівняння. У випадку системи третього порядку (я 3) критичне значення параметру знаходять з розв'язку рівняння М2(Ккр) = 0, /4. Теоретичний аналіз Структурна схема системи автоматичного керування, що досліджується в дан роботі, може бути зведена до найпростішої.
Динамічні властивості багатьох об'єктів керування описуються передаточно функцією
Передаточна функція керуючого пристрою для випадку П-регулятора
' /4. За цих умов, передаточна функція розімкнутої системи
Передаточну функцію замкнутої системи знаходять за формулою
порядок і згідно з критерієм стійкості Гурвіца, не може втратити стійкості при додатних значеннях параметрів системи. Знайдемо вираз для знаходження критичного значення передачі системи I-регулятором. Передаточна функція І-регулятора має вигляд
Передаточна функція розімкнутої системи
Характеристичне рівняння досліджуваної системи автоматичного керування з 1-регулятором згідно з /4.34/ має вигляд
Складемо визначник Гурвіца
Прирівнявши другий мінор визначника до нуля
Отже, критичний коефіцієнт передачі регулятора залежить від параметрів об'єкта, передачі об'єкта, критичний коефіцієнт при чому зі збільшенням коефіцієнта передачі об'єкта, критичний коефіцієнт зменшується. Тепер знайдемо вираз для критичного коефіцієнта передачі з ПІ-регулятором, К який має передаточну функцію: Амплітудно-фазову частотну характеристику отримаємо з передаточної фунта розімкиутої системи шляхом заміни s =jω
При Систему з постійним запізненням при
то для системи із запізненням можна записати
]. Із останнього виразу вадно, що для побудови годографа
Рис. 2. Побудова годографа амплітудно-фазової / v характеристики системи з постійним запізненням. Знаючи запас стійкості граничної системи за фазою у легко розрахуват критичне значення запізнення, при якому система виходить на межу стійкості
де
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.25.152 (0.013 с.) |

 (s) = (W3(0)-W3(s))G(s)
(s) = (W3(0)-W3(s))G(s)













 /4.
/4. /4.
/4.
 дійсна і уявна частина і кореня.
дійсна і уявна частина і кореня.

 = 0,1 с Повторіть розрахунок, а дані занесіть в табл. 2.
= 0,1 с Повторіть розрахунок, а дані занесіть в табл. 2.



 /4. 1
/4. 1 /4.11/ Таким чином, система автоматичного керування з П-регулятором має другий
/4.11/ Таким чином, система автоматичного керування з П-регулятором має другий /4.12/
/4.12/ /4.13/ Відповідно вираз для передаточної функції замкнутої системи буде
/4.13/ Відповідно вираз для передаточної функції замкнутої системи буде /4 14/
/4 14/

 Розв'язок цього рівняння відносно Ккрі дає:
Розв'язок цього рівняння відносно Ккрі дає:
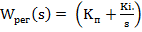

 =0
=0 


 необхідї кожен вектор характеристики 4(©,:) повернути на кут
необхідї кожен вектор характеристики 4(©,:) повернути на кут  =
=  за годинниковою стрілкою. В результаті годограф амплітудно-фазової характеристики системи запізненням деформується і наближається до критичної точки (-1;j0), а за запас стійкості системи зменшується, як це показано на рис. 2
за годинниковою стрілкою. В результаті годограф амплітудно-фазової характеристики системи запізненням деформується і наближається до критичної точки (-1;j0), а за запас стійкості системи зменшується, як це показано на рис. 2

 - частота зрізу.
- частота зрізу.


