
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Робота 7. Аналіз роботи нелінійної системи методом припасовуванняСодержание книги
Поиск на нашем сайте
■ Мета роботи
Вивчити методику побудови математичної моделі нелінійної системи на осно її принципової схеми, ознайомитися з методами побудови перехідних процесів нелінійних системах методом припасовування. Теоретичний аналіз
Нарис, 1. наведена схема нелінійної системи регулювання рівня рідини, Схе» складається з об'єкта регулювання і релейного регулятора,
Об'єктом регулювання є резервуар з постійною витратою рідини. Його динамічні властивості описуються передаточною функцією інтегруючої ланки
Об'єкт регулювання входить до лінійної частини нелінійної системи. u релейний регулятор складається з давачів рівня, аналізуючого і підсилююче? пристрою, релейного елемента і помпи. Статична характеристика регулятор (рис.2.) - куcочно-лінійна з зоною неоднозначності шириною 2h,
6.7. контрольні запитання 1. Що розуміють під терміном якість регулювання? 2. Які існують методи оцінки якості регулювання? 3. Дайте визначення інтегральної квадратичної оцінки якості регулювання? 4. Які існують методи розрахунку інтегральної квадратичної оцінки якості регулювання? 5. Поясніть методику розрахунку інтегральної квадратичної оцінки якості регулювання в даній роботі. 6. Поясніть причину виникнення мінімуму квадратичної інтегральної оцінки при зміні 7. Як використовуються інтегральні оцінки якості? 8. З якої умови знаходяться оптимальні значення коефіцієнтів передачі регуляторів? 9. Як в роботі експериментально визначається інтегральна оцінка якості?
Робота 3. Дослідження частотних характеристик типових ланок Мета роботи За допомогою системи автоматичного моделювання та параметричних оптимізації SIAM дослідити частотні характеристики пропорційної, інтегруючі диференціюючої, аперіодичної та коливної ланок. Теоретичні відомості Одержати математичну модель ланки чи системи автоматичного керуванні можна за її частотними характеристиками, отриманими, наприклад експериментальним шляхом. Частотні характеристики описують передаточні властивості елементів і систем режимі усталених коливань, викликаних вхідним гармонічним сигналом. Нехай на вхід лінійної ланки подано гармонічну дію з циклічною частотою і та з початковою фазою рівною нулю: x(t) = Xsіnωt, У комплексній формі амплітуду вхідного сигналу можна представити виразом: X = X(ω)ej0. Враховуючи, що синусоїдальному коливанню відповідає обертання радіус вектора X з кутовою швидкістю ω, для зображення вхідного сигналу можна записати:
По закінченню перехідного процесу вихідна величина буде змінюватися: гармонічним законом з тією ж частотою, що і вхідна величина, але з іншим амплітудою і початковою фазою:
При зміні частоти вхідного сигналу амплітуда вихідного сигналу і його фа змінюються, тобто є функціями частоти. Зображення вихідного сигналу можі записати у формі:
Відношення зображення гармонічного вихідного сигналу до зображені гармонічного вхідного сигналу називають комплексним коефіцієнтом передачі, або амплітудно-фазовою частотною характеристикою:
Після підстановки:
Залежність
показує як змінюється відставання (випередження) вихідного сигналу від вхідного за фазою яке створює ланка при зміні частоти вхідного сигналу. Для визначення типу динамічних ланок і їх параметрів найбільше поширення отримали логарифмічні частотні характеристики. Вони складаються із логарифмічної амплітудної частотної характеристики L(ω) і логарифмічної фазової частотної характеристики визначається рівністю: L(ω)=20 lg A(ω). При побудові логарифмічних частотних характеристик величина L(ω), що має розмірність - децибели, відкладається по осі ординат в лінійному масштабі. По осі абсцис відкладається кутова частота ω у логарифмічному масштабі або її десятковий логарифм. Інтервал частот, який відповідає збільшенню частоти у десять разів називають декадою. При побудові логарифмічної фазової частотної характеристики змінюється масштаб по вісі частот, а масштаб по вісі ординат залишається незмінним. Характеристики L(ω)і Асимптотичними логарифмічними амплітудними характеристиками називають відрізки асимптот - прямих до яких наближається характеристика L(ω). Графічне представлення амплітудно - фазової характеристики представляється у вигляді годографа. Годографом амплітудно - фазової характеристики називають криву, яку описує кінець радіус вектора A(ω). при зміні частоти від 0 до сю, Побудову годографа можна вести як у полярних координатах за значеннями A(ω). і Програма роботи 1. Побудувати і зарисувати логарифмічні частотні характеристики та годограф пропорційної ланки. 2. Побудувати і зарисувати логарифмічні частотні характеристики та годограф інтегруючої ланки. 3. Побудувати і зарисувати логарифмічні частотні характеристики та годограф реальної диференціюючої ланки. 4. Побудувати і зарисувати логарифмічні частотні характеристики та годограф аперіодичної ланки. 5. Побудувати і зарисувати логарифмічні частотні характеристики та годограф коливної ланки. Варіанти параметрів ланок задайте згідно табл. 1. (Робота 2).
Порядок виконання роботи 1. За формулами /1/ і / 2/ розрахувати оптимальні коефіцієнти передачі, u забезпечують мінімум інтегральної оцінки згідно з варіантом. Дані до розрахункі приведено в табл. 1.
2. Робота виконується за допомогою ЕОМ з використанням програми автоматичної моделювання і параметричної оптимізації SIAM. Зберіть схему дослідження якості регулювання в лінійній системі згідно рисі. Задайте параметри ланок згідно з варіантом. Встановіть величину вхідноїсигналу 0.5 х 1(t). Змініть значення
3. Аналогічним чином зніміть залежності квадратичної інтегральної оцінки в значення настоюваного параметра
За даними табл. 2 і табл. З побудуйте графіки залежностей I0=f(Ki), визнач' оптимальні значення коефіцієнтів і порівняйте з розрахунковими. 4. Перейдіть в режим моделювання клавішею F7 та зніміть перехід характеристики системи з різними регуляторами при оптимальних уставка П-регулятор
І регулятора
ПІ регулятора
Значення коефіцієнтів помилки:
Підставивши значення коефіцієнтів у формулу для інтегральної квадратичної оцінки знаходимо:
Прирівнюючи першу частинну похідну від квадратичної інтегральної оцінки до нуля:
і опускаючи проміжні розрахунки отримуємо вираз для оптимального значення Кі.опт, Що забезпечує мінімум інтегральної квадратичної оцінки:
Тут прийнято, що Т0! — Т02 = Т Аналогічні розрахунки дають вираз для розрахунку оптимального коефіцієнта передачі у випадку ПІ-регулятора:
Програма роботи 1. Розрахувати оптимальні коефіцієнти передачі, що забезпечують мінімум інтегральної оцінки якості регулювання. 2. Зняти експериментальну залежність інтегральної оцінки якості від величини коефіцієнта передачі І-регулятора та визначити оптимальне значення коефіцієнта. 3. Зняти експериментальну залежність інтегральної оцінки якості від величини коефіцієнта передачі ПІ-регулятора та визначити його оптимальне значення. 4. Зняти перехідні характеристики системи при оптимальних значеннях уставок регуляторів. 6.5. Схема дослідження
Порядок виконання роботи 1. Завантажте в комп'ютер програму автоматичного моделювання і параметричної оптимізації SIAM. Для побудувати логарифмічних частотних характеристик пропорційної лані при допомозі функціональної клавіші F2 головного меню програми переведіть систему в режим вводу моделі. З набору типових блоків виберіть ланку передаточною функцією К та задайте величину К згідно з варіантом; Натисканням клавіші Esc поверніться до головного меню програми. За допомого функціональної клавіші F9 переведіть систему в режим побудови частотні характеристик. В лівому нижньому вікні екрана з клавіатури наберіть команду L =А,, де А - ідентифікує ланку для якої здійснюється побудова частотні характеристик. Після виконання команди у вікні оперативного контролю будують частотні характеристики ланки. Збільшення масштабу графіка здійснюється допомогою функціональної клавіші F3. З екрана монітора зарисуйте логарифмічі амплітудно-частотну (на графіку виділена потовщеною лінією) і фазово-частоті характеристики пропорційної ланки разом з системою координат. Для побудови годографа амплітудно-фазової частотної характеристики натисніть функціональну клавішу F4. З екрана монітора зарисуйте систему координат та годограф амплітудно-фазової частотної характеристики пропорційна ланки. /Для всіх ланок необхідно змінювати діапазон розрахунку та побудови, шляхом зміни частоти натисканням клавіші F2 після побудови частотних характеристики (необхідно виставити значення логарифма кінцевої частоти рівним 13). 2. Аналогічним чином побудуйте і зарисуйте частотні характеристики інтегруючої ланки, вибравши з типових блоків блок з передаточною функціє
3. Дія побудови частотних характеристики реальної диференціюючої ланки типових блоків виберіть блок з передаточною функцією Для наближення властивостей реальної диференціюючої ланки до ідеали задайте постійну часу невелику, наприклад Т = 0.0001 с. 4. Аналогічним чином побудуйте і зарисуйте частотні характеристики аперіодичної ланки, вибравши з типових блоків блок з передаточною функцією
5. Аналогічним чином побудуйте і зарисуйте частотні характеристики коливі ланки, вибравши з типових блоків блок з передаточною функції
Загальне зауваження: при заданні параметрів ланок початкові умови залиште нульовими.
3.5. Контрольні запитання 1. Дайте означення комплексного коефіцієнта передачі ланки? 2. Які існують види частотних характеристик? 3. Які методи визначення частотних характеристик Ви знаєте? 4. Дайте означення годографа амплітудно-фазової частотної характеристики. 5. Яка методика побудови годографа амплітудно-фазової частотної характеристики. 6. Яка методика побудови логарифмічних частотних характеристик? 7. Які характеристики називають асимптотичними логарифмічними? 8. Яка методика визначення параметрів ланок за їх логарифмічними частотними характеристиками? 9. Які лайки називають мінімально-фазовими? 10. Яка властивість мінімально-фазових ланок?
Інтегральну оцінку може бути виражена через зображення Лапласа від динамічної помилки системи
Для розрахунку квадратичної оцінки за зображенням динамічної помилки і практиці використовують формулу Релея, або формули отримані Мак-Леном. Ма Леном знайдено інтеграли для систем різного порядку, в яких степінь поліно* чисельника менший на одиницю за степінь полінома знаменника,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.17 (0.007 с.) |

 Рис. і. Нелінійна система автоматичного регулювання рівня рідини.
Рис. і. Нелінійна система автоматичного регулювання рівня рідини.






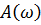 рівну відношенню амплітуд вихідного і вхідного сигнал називають амплітудною частотною характеристикою. Вона показує, як ланка або система пропускає сигнали різної частоти. Фазова частотна характеристика
рівну відношенню амплітуд вихідного і вхідного сигнал називають амплітудною частотною характеристикою. Вона показує, як ланка або система пропускає сигнали різної частоти. Фазова частотна характеристика 
 будують одна під одною, або в одній системі координат. Перевагами логарифмічних характеристик є зручніший масштаб та можливість замінити операцію перемноження амплітудних характеристик їх додаванням при послідовному з'єднанні ланок.
будують одна під одною, або в одній системі координат. Перевагами логарифмічних характеристик є зручніший масштаб та можливість замінити операцію перемноження амплітудних характеристик їх додаванням при послідовному з'єднанні ланок.
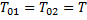
 та повторіть моделювання. Дазалежності квадратичної інтегральної оцінки від значення настоюваного параметри
та повторіть моделювання. Дазалежності квадратичної інтегральної оцінки від значення настоюваного параметри  і
і  беремо з формули для зображення динамічної
беремо з формули для зображення динамічної


 ,
, 
 ,
, 




 Рис. 1. Схема дослідження
Рис. 1. Схема дослідження






