
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коливання струни: виведення хвильового рівняння.Содержание книги
Поиск на нашем сайте
Коливання струни: виведення хвильового рівняння. Розглянемо такі коливання струни з закріпленими кінцями. Зробимо такі припущення: 1. Струна туго натягнута; 2. Струна зроблена з однорідного матеріалу; 3. Струна коливається в одній площині; 4.
Виявляється, що хвильове рівняння є законом руху Ньютона (зміна імпульсу дорівнює силі діючих сил). Уявимо собі ті сили, що діють на струну у напрямках перпендикулярних до осі ОХ: 1. Сила, обумовлена натягом струни:
Сила =Т
2. Зовнішня сила, може довільним чином залежати від часу і просторової змінної: F(t, x) – mg 3. Сили тертя. Якщо струна коливається у певному середовищі, то виникає сила опору пропорційна силі струни. 4. Повертаючи сила. Ця сила направлена проти зміщення струни, якщо u> 0, то сила від’ємна. Прикладемо тепер рівняння руху Ньютона до невеличкої ділянки
Спрямуємо
де
Рівняння (1) є добре відомим у різних прикладаннях телеграфним рівнянням. Найпростіше хвильове рівняння
Задачу (2) і (3) наз задачею Коші для хвильового рівняння.
ФОРМУЛА д’АЛАМБЕРА (розв’язування задачі Коші для хвильового рівняння) Розглянемо задачу Коші для одновимірного хвильового рівняння (ДРЧП) (ПУ) Розв’язування задачірозіб’ємо на кроки. Крок 1. Заміна координат t, x новими канонічними координатами Крок 2. Розв’язування перетвореного рівняння:
Отже, загальний розв’язок рівняння
Крок 3. Повернення до початкових координат t, x. Для знаходження загального розв’язку рівняння (4) підставимо
в розв’язок (5). В результаті отримаємо
Це загальний розв’язок рівняння (4 Крок 4. Врахування початкових умов.
Для розв’язування задачі Коші (4) підставимо загальний розв’язок (6) хвильового рівняння (який містить дві довільні функції) в початкові умови, щоб знайти конкретні вирази для функцій Проінтегрувавши другу рівність в межах від
Тоді із (7) і (8) отримуємо
а тому
РОЗВ’ЯЗУВННЯ ЗМІННОЇ ЗАДАЧІ ДЛЯ НАПІВНЕСКІНЧЕННОЇ СТРУНИ ЗА ДОПОМОГОЮ ФОРМУЛИ д’АЛАМБЕРА Поставимо перед собою задачу: знайти хвильові рухи напівнескінченної струни, лівий кінець якої жорстко закріплено при даних початкових умовах. Тут є додаткова гранична умова (ГУ), а тому задача має такий вигляд: (ДРЧП) (ГУ) (ПУ) Підставивши загальний розв’язок в початкові умови, маємо
Тепер виникає проблема, якої не було під час розв’язування задачі Коші. Розв’язок На жаль, перша з формул (11) дозволяє обчислювати Якщо
Що робити, коли Підстановка знайденого значення
Комбінуючи розв’язки для
Загальні властивості крайових задач Розглянемо стаціонарний (при (ДРЧП) (ГУ) Щоб знайти стаціонарний розв’язок
Коливання струни: виведення хвильового рівняння. Розглянемо такі коливання струни з закріпленими кінцями. Зробимо такі припущення: 1. Струна туго натягнута; 2. Струна зроблена з однорідного матеріалу; 3. Струна коливається в одній площині; 4.
Виявляється, що хвильове рівняння є законом руху Ньютона (зміна імпульсу дорівнює силі діючих сил). Уявимо собі ті сили, що діють на струну у напрямках перпендикулярних до осі ОХ: 1. Сила, обумовлена натягом струни:
Сила =Т
2. Зовнішня сила, може довільним чином залежати від часу і просторової змінної: F(t, x) – mg 3. Сили тертя. Якщо струна коливається у певному середовищі, то виникає сила опору пропорційна силі струни. 4. Повертаючи сила. Ця сила направлена проти зміщення струни, якщо u> 0, то сила від’ємна. Прикладемо тепер рівняння руху Ньютона до невеличкої ділянки
Спрямуємо
де
Рівняння (1) є добре відомим у різних прикладаннях телеграфним рівнянням. Найпростіше хвильове рівняння
Задачу (2) і (3) наз задачею Коші для хвильового рівняння.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.43 (0.01 с.) |



 х
х



 і отримаємо
і отримаємо 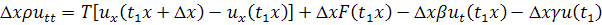
 – лінійна густина струни;
– лінійна густина струни; – деякі лінійні коефіцієнти;
– деякі лінійні коефіцієнти;
 і перейдемо до границі, в результаті отримаємо рівняння:
і перейдемо до границі, в результаті отримаємо рівняння: (1)
(1)
 (2). Оскільки рівняння (2) містить похідну за часом 2-го порядку, то для отримання єдиного розв’язку при t
(2). Оскільки рівняння (2) містить похідну за часом 2-го порядку, то для отримання єдиного розв’язку при t  потрібно знати 2 початкові умови: початкове зміщення струни і початкову швидкість струни
потрібно знати 2 початкові умови: початкове зміщення струни і початкову швидкість струни (3)
(3) (3)
(3)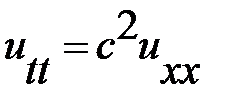 ,
, 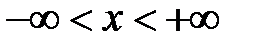 ,
, 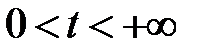

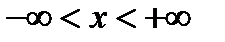
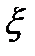 ,
,  :
: 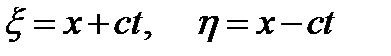 ,які зводять рівняння до вигляду
,які зводять рівняння до вигляду 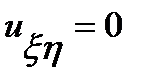 .
.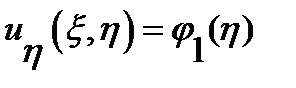 довільна функція змінної
довільна функція змінної 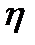 ,
, 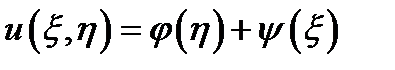 ,
,  .
.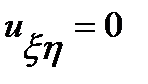 записується у вигляді
записується у вигляді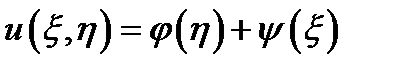 .
.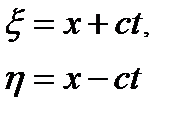
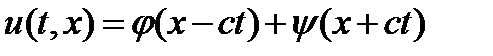
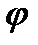 і
і  . Маємо:
. Маємо: 
 до
до  , отримаємо
, отримаємо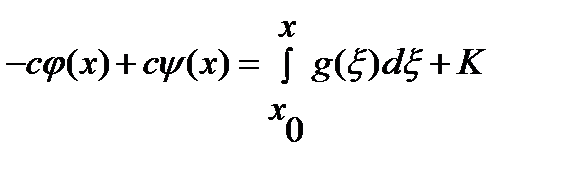
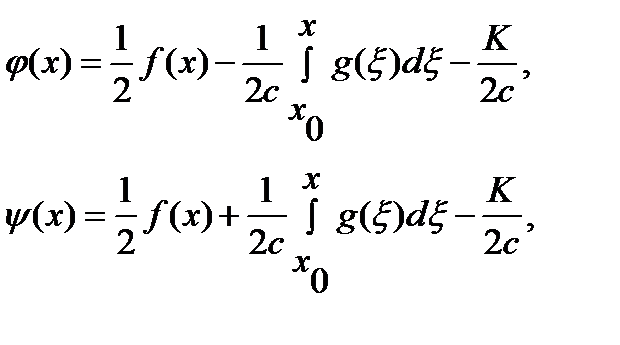
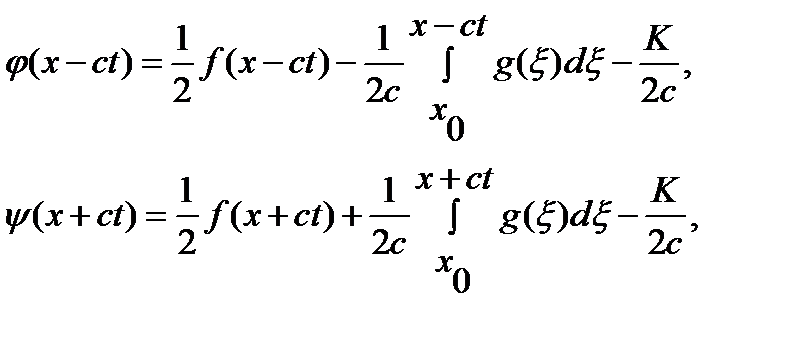 отже,
отже,  .Розв’язок називають формулою д’Аламбера.
.Розв’язок називають формулою д’Аламбера.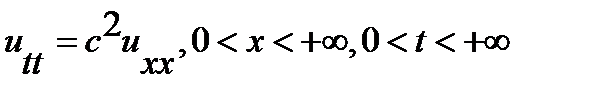 ,
, ,
,
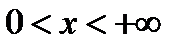 .
.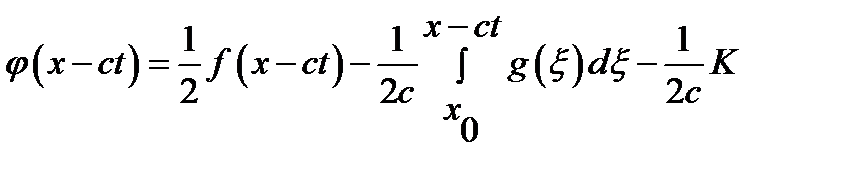
 .
. повинен бути визначеним скрізь лише всередині першого квадранта
повинен бути визначеним скрізь лише всередині першого квадранта 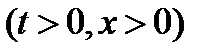 площини змінних
площини змінних 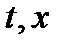 . Отже, ми повинні вміти обчислити значення функції
. Отже, ми повинні вміти обчислити значення функції  для всіх
для всіх 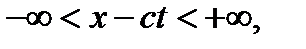 а значення функції
а значення функції 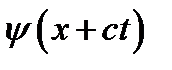 для всіх
для всіх 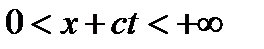 .
.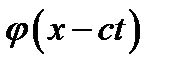 лише для
лише для 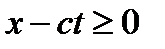 , оскільки в початкових умовах функції f(x) та g(x) визначені лише для додатних значень аргумента.
, оскільки в початкових умовах функції f(x) та g(x) визначені лише для додатних значень аргумента. , то
, то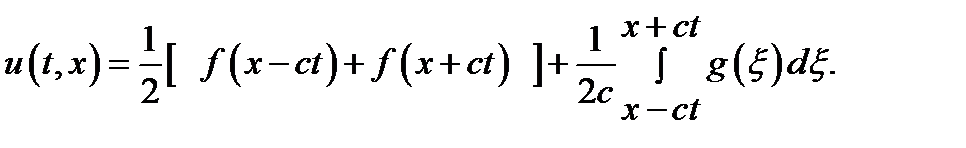
 ? Для цього скористаємося граничною умовою
? Для цього скористаємося граничною умовою 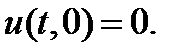 З її допомогою доозначимо функцію
З її допомогою доозначимо функцію  для
для 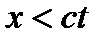 . Підставивши
. Підставивши  в граничну умову отримаємо
в граничну умову отримаємо 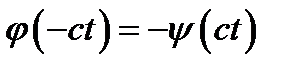 , звідки
, звідки 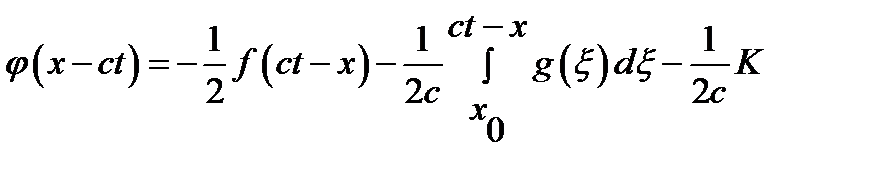 .
.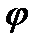 в загальний розв’язок дає
в загальний розв’язок дає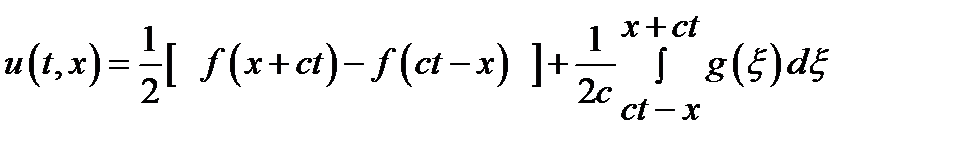 ,
, 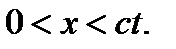
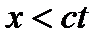 та
та  , нарешті отримуємо
, нарешті отримуємо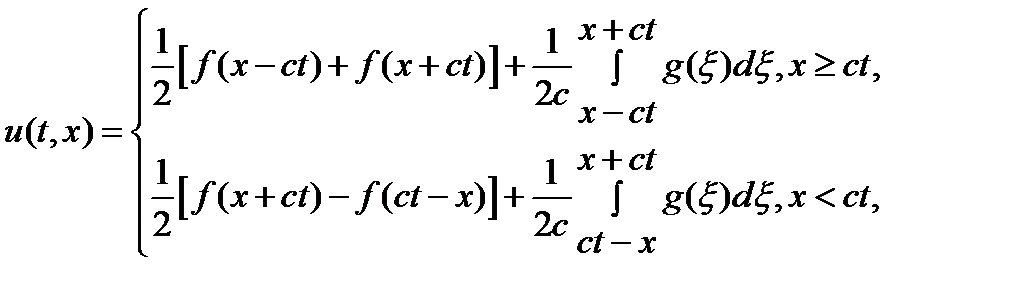 розв'язок задачі.
розв'язок задачі. ) розв’язок рівняння теплопровідності
) розв’язок рівняння теплопровідності  Оскільки розв’язок не змінюється з плином часу, то
Оскільки розв’язок не змінюється з плином часу, то  і рівняння теплопровідності переходить в рівняння Лапласа
і рівняння теплопровідності переходить в рівняння Лапласа 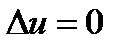 . Розглянемо задачу
. Розглянемо задачу
 ,
,  ,(ПУ)
,(ПУ)  .
. (якщо він існує) покладемо
(якщо він існує) покладемо  і розв’яжемо крайову задачу
і розв’яжемо крайову задачу Її розв’язок має вигляд
Її розв’язок має вигляд 



