
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача Коші для рівняння теплопровідностіСодержание книги
Поиск на нашем сайте
Задача про поширення тепла в необмеженому однорідному стержні, бічна поверхня якого теплоізольована, математично формулюється так. Знайти обмежену функцію
Покласти Підставивши
або, змінивши порядок інтегрування, Тому
Диференціюючи інтеграл
Інтегруючи за частинами, отримуємо
Підставивши знаходимо 13. Граничні умови в задачах дифузійного типу 1. Гу І-го роду (на кінці задано t); Розглянемо теплову енергію у одновимірному просторі:
U(t,0)=g1(t); U(t,L)=g2(t); Задачі з ГУ І-го роду зустрічаються досить часто. У деяких випадках суть задачі полягає у тому, щоб знайти керування ГУ, тобто такі g1(t), та g2(t), що змушують температуру в середині стержня змінюватися заданим чином. 2. ГУ- ІІ-го роду
Задаючи ГУ цього типу ми не можемо вважати граничною температурою стержня такою, як у середовищі, але ми знаємо закон Ньютона. Якщо t одного кінця стержня менша ніж на другому кінці, то тепло буде надходити у стержень зі швидкістю, яка пропорційна різниці температур в.т.т.л.к=h [U(t,0)-g1(t)]; в.т.т.л.к==h [U(t,L)-g2(t)]; h- коєфіцієнт теплообміну. Отримані рівності разом із законом теплопровідності Фур’є можна використати для запису граничних умов. Закон Фур’є: Течія тепла, яка проходить через межу області є пропорційною нормальній похідній у напрямку внутрішньої нормалі в.т.т.л.к=k в.т.т.л.к=- k k – коєфіцієнт теплопровідності Можемо записати ГУ у математичному вигляді. Маємо:
3. ГУ ІІІ-го роду. Задано течію, зокрема включимо випадок теплоізольваних меж. Через теплоізольовані межі не проходить ніяка течія, а тому нормальна похідна на межі має набувати нульового значення. Ux(t,0)=0; Ux(t,L)=0. 0<t<+∞; 14. Хвильове рівняння і граничні умови Ми розглянули один тип руху- коливання струни, але у природі існують і інші: - звукові хвилі (подовжні); - електромагнітні (світлові); - коливання твердих тіл (подовжні,поперечні та крутильні); - хвилі ймовірності у Квантовій механіці; - хвилі ні воді. Зупинимося на різних типах ГУ, які виникають під час розв’язування задач хвильового характеру. Будемо розглядати лише одновимірні задачі, та ГУ (лінійні). Як правило розрізняють ГУ 3-ох типів: 1. Задача режиму у граничних точках 0,L (ГУ І-го роду) U(t,0)=g1(t); U(t,l)=g2(t); 2. Задано сили у граничних точках (ГУ ІІ-го роду) Ux(t,0)=g1(t); Ux(t,L)=g2(t); 3. Пружне закріплення у граничних точках. Ux(t,0) – Ux(t,1) - Розглянемо приклад: 1. Нехай мають місце ГУ І-го роду, тоді має місце L=1. У цьому випадку виникає задача: Utt=c2Uxx,0<x<1, t>0; Далі маємо дві граничні умови: U(t,0)= g1(t) t>0; U(t,l)=g2(t) І дві початкові умови: U(0,x)=f(x); 0<x<1; Ut(0,x)=g(x) Характерною задачею є крутильні коливання стержня, лівий кут якого закріплений, а правий повертається на деякий кут. Однією із важливих задач є задача визначення такої функції g2(f), щоб за мінімальний час погасити коливання струни. 2. Задано сили у граничних точках.
Вершини сил, які діють на лівий та правий кінці струни визначаються виразом:
TUx(t,0), TUxx(t,1). Якщо кінець переміщується уздовж вертикальних направляючих без тертя то ГУ набувають такого вигляду: Ux(t,0)=0 Ux(t,l)=1 ГУ такого типу виникають наприклад у подовжніх коливаннях пружини з вільним кінцем і коливання пружини під дією сили, яку прикладено до одного кінця. 3. Пружини закріплення кінців. Нехай h- коєфіцієнт пружності кінців.
Зусилля, що створюються пружинами на кінцях струни такі: Лівий кінець- TUx(t,0) Правий - TUxx(t,l) Враховуючи h маємо такі ГУ: Ux(t,0)=h/T U(t,0) Ux(t,1)=- h/T U(t,1) Або Ux(t,0)-h/T U(t,0)=0 Ux(t,0)-h/T U(t,1)=0 Для ДРЧП будь-якого типу розрізняють в залежності від типу ГУ І, ІІ, та ІІІ-тю крайові задачі. Якщо у правих точках мають місце ГУ різних типів, то задачі називають змішаними крайовими задачами.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.97 (0.01 с.) |

 (
( ), яка задовольняє рівнянню теплопровідності
), яка задовольняє рівнянню теплопровідності  (
( ) і ПУ
) і ПУ  (
( ), де
), де 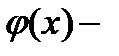 неперервна обмежена функція. Скориставшись методом відокремлення змінних, отримуємо:
неперервна обмежена функція. Скориставшись методом відокремлення змінних, отримуємо: , де
, де  довільний параметр. Проінтегрувавши (9) за параметром
довільний параметр. Проінтегрувавши (9) за параметром 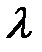 отримаємо:
отримаємо: . Поклавши
. Поклавши  , отримаємо
, отримаємо  . Порівнявши:
. Порівнявши:
 ,
,  .
.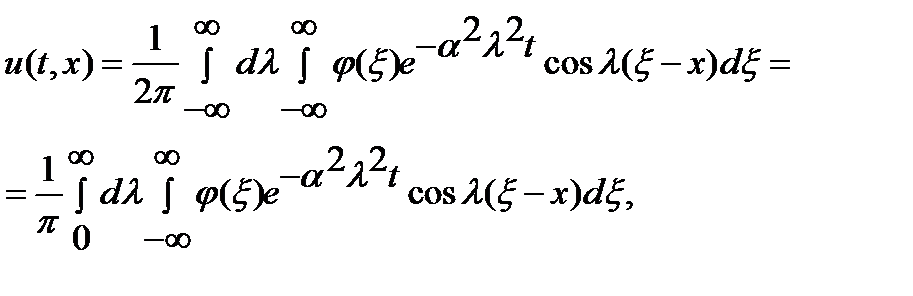
 Внутрішній інтеграл можна обчислити. Дійсно, покладемо
Внутрішній інтеграл можна обчислити. Дійсно, покладемо 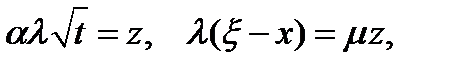 Звідки
Звідки 
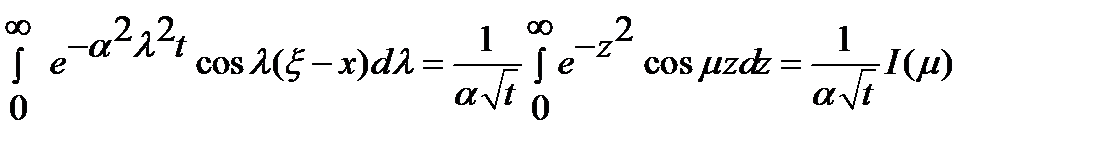
 за параметром
за параметром  , знаходимо, що
, знаходимо, що
 , Звідки
, Звідки  . Щоб знайти сталу С, покладемо тут
. Щоб знайти сталу С, покладемо тут  . Це дає
. Це дає . Отже
. Отже  , і
, і  .
. Формулу називають формулою Пуассона. Вона є розв’язком задачі Коші.
Формулу називають формулою Пуассона. Вона є розв’язком задачі Коші.
 =s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>k</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
=s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>k</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  [U(t,0)-g1(t)];
[U(t,0)-g1(t)]; =-s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>k</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
=-s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>k</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  1 U(t,0)=g1(t);
1 U(t,0)=g1(t);


