
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 14. Вимушені коливання механічної системи з одним ступенем вільності з врахуванням лінійного опору.Содержание книги
Поиск на нашем сайте
Література: [2] Гл. 7. §2. [4] Гл. 2.5. [3] §6–8. § 14.1. Постановка задачі. Система має один ступень вільності. Вивчаємо рух механічної системи поблизу положення стійкої рівноваги. На систему діють сили: – потенціальні; – сили лінійного опору; – збурюючі сили. Ми отримали узагальнену збурюючу силу
δ – початкова фаза; р – частота сили.
Знайдемо похідні: Тоді (14.1) має вигляд Поділимо на а і введемо позначення
§ 14.2. Інтегрування диференціального рівняння руху. Закон руху. Диференціальне рівняння (14.2) – ЛНДР – лінійне неоднорідне диференціальне рівняння ІІ порядку з постійними коефіцієнтами. Його розв’язок
Де:
Згадаємо тему 11,
Праву частину рівняння (14.2) перетворимо так
Аналізуючи (14.8) відмітимо властивості вимушених коливань. § 14.3. Властивості вимушених коливань. 1. Навіть при наявності опору вимушені коливання носять періодичний, незатухаючий характер. 2. Частота і період вимушених коливань дорівнюють частоті і періоду збурюючої сили. 3. Амплітуда В (формула (14.6)) і початкова фаза ε (формула (14.7)) не залежать від початкових умов, а залежать від: вихідних параметрів а і с, частоти р збурюючої сили та сили опору. Амплітуда залежить ще від амплітуди збурюючої сили Н.
4. Навіть при резонансі (ω=р) при наявності лінійного опору амплітуда має конкретне значення В≠∞. Далі розглянемо окремо важливе для інженерної практики питання. § 14.4. Залежність амплітуди та фази вимушених коливань від частоти та фази збурюючої сили. Розглянемо більш детально формулу амплітуди вимушених коливань. Перетворимо (14.6) так: поділимо на ω2 чисельник і знаменник
- коефіцієнт динамічності. З’ясуємо зміст
Дослідимо знаменник
Висновки. 1. При наявності лінійного опору найбільше значення λ досягає не при z=1, тобто не при резонансі, а при z<1, якщо 2. Чим менший опір d, тим більша λmax. λ зростає тим швидше, чим менше d. 3. Для великих частот збурюючої сили амплітуда вимушених коливань невелика. 4. Сили опору мають вплив на амплітуду лише поблизу резонансної зони, розміром в 30%. 5. Для частот, що знаходяться за тридцятипроцентною резонансною зоною, вплив сил опору малопомітний. Тобто для z<0,7; z>1,3, коефіцієнт динамічності λ≤2. 6. Для d>0,7 максимальне значення амплітуди дорівнює її статичному значенню, і резонансу не буває. Дослідимо зсув фаз вимушених коливань відносно збурюючої сили, тобто формулу(14.7)
Звертаю увагу на те, що як і в випадку відсутності лінійного опору (рис.13.5) так і при наявності малого лінійного опору (рис.14.2) зсув фаз при резонансному дорівнює π/2. Питання для самоконтролю. 1. В яких рівновагах може знаходитися механічна система? 2. Яка рівновага механічної системи називається стійкою?
3. Сформулюйте теорему Лагранжа-Діріхле. 4. Достатньою чи необхідною умовою стійкості рівноваги є теорема Лагранжа-Діріхле? 5. За якими формулами розраховуються кінетична, потенціальна енергії і функція Релея системи, що здійснює малі рухи біля положення стійкої рівноваги? 6. Запишіть диференціальне рівняння власних коливань механічної системи з одним ступенем вільності без врахування сил опору. 7. За яким законом здійснюються власні коливання механічної системи з одним ступенем вільності при відсутності сил тертя? 8. Як визначають амплітуду і початкову фазу власних коливань механічної системи? 9. За якою формулою розраховується період вільних коливань механічної системи? 10. Які сили називаються дисипативними? 11. За якою формулою визначається функція Релея? 12. За якою формулою розраховується узагальнена сила дисипативних сил? 13. Як зв’язана функція Релея з механічною енергією системи? 14. Запишіть диференціальне рівняння власних коливань механічної системи з одним ступенем вільності з врахуванням сили лінійного опору. 15. При якій силі опору коливний рух механічної системи переходить в аперіодичний? 16. Запишіть рівняння затухаючих коливань механічної системи з одним ступенем вільності. 17. Як впливає сила опору на період власних коливань механічної системи? 18. За яким законом змінюється амплітуда затухаючих коливань механічної системи? 19. Що називається декрементом коливань і за якою формулою він знаходиться? 20. Запишіть диференціальне рівняння вимушених коливань механічної системи з одним ступенем вільності. 21. Зі скількох частин складається загальний розв’язок диференціального рівняння вимушених коливань і що визначає кожна з цих частин? 22. Чи залежить частота власних коливань системи від параметрів збурюючої сили? 23. З якою частотою здійснюються вимушені коливання механічної системи? 24. За якою формулою розраховується початкова фаза вимушених коливань механічної системи? 25. В якому випадку початкова фаза вимушених коливань дорівнює нулю? 26. Що характеризує коефіцієнт динамічності? 27. В якій області частот система найбільш чутлива до дії збурюючої сили? 28. За якої умови виникає резонанс? 29. Як змінюється амплітуда вимушених коливань системи при резонансі без врахування сили опору?
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.116.226 (0.01 с.) |

 Н – амплітуда сили;
Н – амплітуда сили;
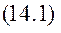 Складаємо диференціальне рівняння руху, скориставшись рівнянням Лагранжу ІІ роду. q – узагальнена координата. Наближені значення кінетичної і потенціальної енергії
Складаємо диференціальне рівняння руху, скориставшись рівнянням Лагранжу ІІ роду. q – узагальнена координата. Наближені значення кінетичної і потенціальної енергії 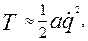
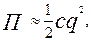 а, с – коефіцієнти інерції та жорсткості, відповідно. Дисипативна функція
а, с – коефіцієнти інерції та жорсткості, відповідно. Дисипативна функція  , b – узагальнений коефіцієнт опору. Рівняння Лагранжу ІІ роду має вигляд (10.3)
, b – узагальнений коефіцієнт опору. Рівняння Лагранжу ІІ роду має вигляд (10.3) ,
,  ,
,  ,
, 
 .
. ,
,  ,
,  (*)
(*)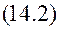 Диференціальне рівняння руху
Диференціальне рівняння руху

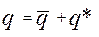
 – загальний розв’язок однорідного рівняння
– загальний розв’язок однорідного рівняння
 Розглянемо випадок малого опору n<ω, тоді
Розглянемо випадок малого опору n<ω, тоді де
де 

 – частинний розв’язок рівняння (14.2), вид якого диктується його правою частиною. В даному випадку
– частинний розв’язок рівняння (14.2), вид якого диктується його правою частиною. В даному випадку
 Через те, що з часом власні коливання зникають (бо є співмножник
Через те, що з часом власні коливання зникають (бо є співмножник  ), можна вважати, що залишаться тільки вимушені коливання, тобто частинний розв’язок
), можна вважати, що залишаться тільки вимушені коливання, тобто частинний розв’язок
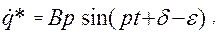 Знайдемо постійну В. Для цього підставимо (14.5) в (14.2), отримавши похідні
Знайдемо постійну В. Для цього підставимо (14.5) в (14.2), отримавши похідні Після підстановки в рівняння (14.2), маємо
Після підстановки в рівняння (14.2), маємо 






 Маємо, зібравши коефіцієнти при
Маємо, зібравши коефіцієнти при  та при
та при  :
: Можна вважати, що для t далекого від початкового
Можна вважати, що для t далекого від початкового 
 і не змінюється.
і не змінюється. Позначимо:
Позначимо: – коефіцієнт розладнання,
– коефіцієнт розладнання, – відносний коефіцієнт опору,
– відносний коефіцієнт опору,

 n<ω, 0<d<1
n<ω, 0<d<1 . Якщо на систему діє постійна сила Н, що дорівнює максимуму збурюючої сили, тоді
. Якщо на систему діє постійна сила Н, що дорівнює максимуму збурюючої сили, тоді  . Частинний розв’язок
. Частинний розв’язок  ,
,  ,
,  ,
,  ,
,  – відхилення системи в положенні рівноваги під дією постійні сили, що дорівнює амплітуді збурюючої сили Тоді
– відхилення системи в положенні рівноваги під дією постійні сили, що дорівнює амплітуді збурюючої сили Тоді  – відношення динамічної амплітуди до статичної називають: коефіцієнт динамічності.
– відношення динамічної амплітуди до статичної називають: коефіцієнт динамічності.




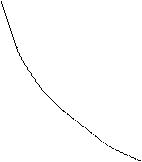











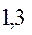








 Замість задачі залежність В(р) вивчимо залежність λ(z) коефіцієнта динамічності від коефіцієнта розладнання. Покажемо графік функції (14.9).
Замість задачі залежність В(р) вивчимо залежність λ(z) коефіцієнта динамічності від коефіцієнта розладнання. Покажемо графік функції (14.9). на екстремум. Для цього отримаємо похідну
на екстремум. Для цього отримаємо похідну 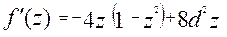 ,
,  ,
,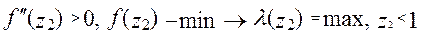
 Прирівняємо
Прирівняємо  , тобто знайдемо значення z при яких буде екстремум
, тобто знайдемо значення z при яких буде екстремум 
 , а саме при
, а саме при 
















 Для z<1
Для z<1 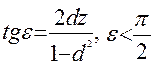
 Для z=1
Для z=1 
 Для z>1
Для z>1 



