
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 10. Вступ в теорію малих лінійних коливань.Содержание книги
Поиск на нашем сайте
Література: [2] Гл. 7. §1. [4] Гл. 11.1. [3] §1–4. § 10.1. Види механічних коливань. Механічні коливання – це найбільш поширений рух механічної системи: транспортні машини, деталі машин, фундаменти, мости, верстати і ін.
    
Розрізняють коливання в залежності від виду деформації, а значить від пружних сил, чи їх моментів. Наприклад: коливання шпиндельного валу. До ріжучого інструменту прикладена сила різання Р(Рx, Рy, Рz).
q2= q3=z


 
 , q3=z. Тому незалежно від виду руху властивості руху зберігаються. , q3=z. Тому незалежно від виду руху властивості руху зберігаються.
§ 10.2. Поняття про стійкість рівноваги. Теорема Лагранжа – Діріхле.
                      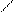 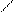 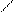 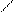   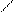       Поставимо собі за мету вивчити характер руху механічної системи з “р” ступенями вільності, на яку накладені голономні в’язі, і діють потенціальні сили поблизу положення стійкої рівноваги. Що таке стійка рівновага? Поставимо собі за мету вивчити характер руху механічної системи з “р” ступенями вільності, на яку накладені голономні в’язі, і діють потенціальні сили поблизу положення стійкої рівноваги. Що таке стійка рівновага?
Нехай в положенні рівноваги всі узагальнені координати Означення по Ляпунову О.М.
Ляпунов О.М. (1857–1919) Харків, 1892р. “Загальна задача про стійкість руху” (докторська дисертація). Є спеціальні теореми про стійкість і нестійкість руху чи рівноваги. Теорема Лагранжа – Діріхле встановлює достатні умови стійкого положення рівноваги. Для стійкого положення рівноваги системи з голономними ідеальними стаціонарними двосторонніми в’язями, що знаходиться в стаціонарному потенціальному силовому полі, достатньо, щоб в цьому положенні рівноваги потенціальна енергія системи мала мінімум.
Приймемо теорему без доведення. Іще розглянемо один приклад на тему “Дослідження стійкої рівноваги”.
Якщо розглянути перше положення, коли точка О знаходиться вгорі, то при любому положенні точки В рівновага стійка. Що буде при другому положенні (точка О внизу)? Зовсім інші результати. В залежності від положення точки В: кулька або повертається в початкове положення, або ні! Для того, щоб з’ясувати при якому значенні координати ОВ=у, положення рівноваги буде стійким, треба знайти потенціальну енергію системи. Потенціальна енергія системи в відхиленому на кут φ положенні дорівнює сумі робіт потенціальних сил при переміщенні з даного положення в нульове (φ=0) Якщо врахувати, що для малих φ § 10.3. Про особливості методу вивчення малих коливань системи. Повинні виконуватись умови (*): - - вивчається рух поблизу положення стійкої рівноваги. Метод вивчення.
2. Кінетичну і потенціальну енергії системи, які входять в рівняння Лагранжу ІІ роду, будемо брати в наближеному вигляді, бо координати
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.73.6 (0.01 с.) |


































 q1=x
q1=x



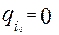 і всі узагальнені швидкості
і всі узагальнені швидкості  . В деякий момент часу t0 виведемо систему з положення рівноваги, тобто задамо
. В деякий момент часу t0 виведемо систему з положення рівноваги, тобто задамо  ,
,  . Якщо при всіх t>t0 координати і швидкості
. Якщо при всіх t>t0 координати і швидкості 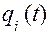 і
і 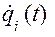 – малі, менші ніж початкові
– малі, менші ніж початкові  Положення рівноваги механічної системи називають стійким, якщо для вибраних довільно досить малих ε1 і ε2 можна вказати такі додатні числа η1 і η2, що при
Положення рівноваги механічної системи називають стійким, якщо для вибраних довільно досить малих ε1 і ε2 можна вказати такі додатні числа η1 і η2, що при всі значення узагальнених координат і швидкостей при довільному досить великому t будуть менші ніж ε1 і ε2, тобто
всі значення узагальнених координат і швидкостей при довільному досить великому t будуть менші ніж ε1 і ε2, тобто
 Нагадаю, що в положенні рівноваги кожна узагальнена потенціальна сила дорівнює нулеві, тому
Нагадаю, що в положенні рівноваги кожна узагальнена потенціальна сила дорівнює нулеві, тому
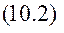 Згадаємо, як дослідити функцію на екстремум. Треба спочатку прирівняти перші похідні нулеві (це і є формули (10.1)), а потім з’ясувати знак других похідних. Якщо йдеться про мінімум, то другі (змішані) похідні повинні бути додатними, тобто
Згадаємо, як дослідити функцію на екстремум. Треба спочатку прирівняти перші похідні нулеві (це і є формули (10.1)), а потім з’ясувати знак других похідних. Якщо йдеться про мінімум, то другі (змішані) похідні повинні бути додатними, тобто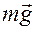


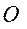

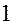












 , маємо
, маємо  . Умова стійкої рівноваги
. Умова стійкої рівноваги  , дає відповідь:
, дає відповідь:  – маємо стійку рівновагу.
– маємо стійку рівновагу.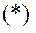 наявність потенціальних сил;
наявність потенціальних сил;
 1. Для отримання диференціальних рівнянь руху механічної системи будемо використовувати рівняння Лагранжу ІІ роду:
1. Для отримання диференціальних рівнянь руху механічної системи будемо використовувати рівняння Лагранжу ІІ роду: і швидкості
і швидкості  – малі величини.
– малі величини.


