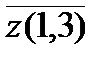Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача коммивояжера. Решение задачи методом ветвей и границ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте задача коммивояжера. Предположим, что наш граф гамильтонов и на его дугах заданы веса cij, которые могут обозначать, например, стоимость проезда между населенными пунктами. Коммивояжер (бродячий торговец) должен побывать во всех этих пунктах и вернуться назад, затратив при этом минимум средств. То есть речь идет о построении гамильтонова цикла минимального веса. В общем случае предполагается, что cij ¹ cji, то есть граф может быть и ориентированным, причем веса дуг (u,v) и (v,u) могут отличаться. Решение задачи «в лоб» предполагает перебор всех возможных вариантов, то есть p! операций. Но если граф большой, это слишком дорогое удовольствие, поэтому разработаны приемы сокращения перебора. Наиболее распространенный из таких методов ограниченного перебора носит название «метод ветвей и границ». Решение задачи коммивояжера методом ветвей и границ. Рассмотрим дерево перебора (дерево решений) и назовем его T, как мы называли упорядоченные корневые деревья. Общий принцип решения методом ветвей и границ такой: на каждом шаге дерево решений разбивается на подмножества ветвей
Рассмотрим, как это выглядит в данной задаче. Будем иллюстрировать рассуждения на полном пятивершинном графе (точнее, ориентированном мультиграфе, где cij ¹ cji) с матрицей весов C. Очевидно, что этот граф гамильтонов. Матрица весов у нас будет следующая: Основной операцией, на основе которой выполняется необходимая оценка, является приведение матрицы весов. Что это означает? Рассмотрим по шагам. Введем обозначения: z – искомый гамильтонов цикл, l (z) – вес такого гамильтонова цикла. Шаг 1. Получение нижней l 0(z) и верхней L (z) оценок веса искомого гамильтонова цикла (построение границ решения). Начнем с получения нижней оценки, так как именно она наиболее важна для решения задачи. 1.1. Выбираем min по каждой строке матрицы весов. Строка i у нас, как всегда, соответствует выходам из вершины vi, а столбец i - входам. То есть мы выбираем сначала минимальный по весу выход из каждой вершины.
Теперь из каждой строки матрицы вычтем соответствующее этой строке минимальное значение. Получаем матрицу:
Если бы в каждом столбце после вычитания оказалось по нулю, это означало бы, что из каждой вершины можно выйти по дуге минимального веса и в каждую вершину можно войти по дуге минимального веса. В этом случае вес гамильтонова цикла был бы равен l 0(z)=6, то есть той сумме, которую мы получили. И задача была бы решена уже на первом шаге. Но у нас в третьем столбце нулей нет. Поэтому придется принять, что l (z)> l 0(z), и продолжать поиск l (z). 1.2. Выбираем min по каждому столбцу, то есть рассматриваем все дуги, по которым можно войти в каждую вершину vj. Повторяем то, что делали на первом шаге, только теперь для столбцов.
Теперь вычитаем из столбцов минимальные значения.
Полученный результат показывает, что минимальная дуга, по которой мы можем войти в вершину 3, - это c 13=2. Теперь уже ясно, что l (z)³ l 0(z)+ c 13=8. Таким образом, мы получили нижнюю оценку веса гамильтонова цикла. То, что мы проделали, называется приведением матриц по строке и столбцу. В приведенной матрице ненулевые значения представляют собой превышения над минимумом при входе и выходе из каждой вершины. 1.3. Для получения верхней оценки L ( z ) построим произвольный цикл методом поиска в глубину и посчитаем его вес по исходной матрице весов. L (z)= c 12+ c 23+ c 34+ c 45+ c 51=1+5+6+4+3=19. Если бы мы получили, что l (z)= L (z), то это и был бы искомый гамильтонов цикл минимального веса. Но в нашем примере это не так. Мы, всего-навсего, имеем 8£ l (z)£19, и нам придется продолжать поиск. Шаг 2. Ветвление (разбиение дерева решений на подмножества). Теперь будем добавлять в цикл по одному ребру на основе следующей схемы. Рассмотрим два случая(рис.3.27).: 1) гамильтонов цикл z проходит через некоторую минимальную по весу дугу (vi, vj); 2) гамильтонов цикл z не проходит через эту дугу. Назовем эти два варианта z (i,j) и Рассмотрим оценки для каждой из этих ветвей. Для ветви z (i,j) остается нижняя оценка l (z)=8. Рассмотрим теперь оценку для ветви
Таким образом, для каждого уже обнуленного перехода по ребру (i,j) можно получить нижнюю оценку превышения над минимумом, если мы пройдем мимо этого ребра.
Вычисляем такие оценки для всех дуг, обнуленных в процессе приведения матрицы, и в качестве альтернативы перехода выбираем вариант с максимальным значением qij. То есть, включаем в цикл то ребро, у которого альтернативный путь Посмотрим, что получается в нашем примере. Для всех нулевых элементов нашей приведенной матрицы cij берем ребро с минимальным значением (по i -й строке), по которому можно выйти из вершины i в любую вершину, кроме j, и ребро с минимальным значением (по j -му столбцу), по которому можно войти в вершину j из любой вершины, кроме i. q 12=0+0=0; q 13=0+1=1; q 14=0+0=0; q21=1+1=2; q 35=1+1=2; q 42=2+0=2; q 54=1+0=1. У нас получилось 3 одинаковых значения, берем первое: q 21. После первого шага z ={(2,1)}. Теперь «склеим» вершины 2 и 1, чтобы вывести дугу (2,1) из рассмотрения. Для этого удалим из матрицы 2-ю строку и 1-й
столбец, учитывая направление дуги в цикле. Получим матрицу весов меньшей размерности. В этой матрице заменим элемент c 21 на символ ¥, чтобы про него забыть, поскольку назад от 1 к 2 мы уже переходить не имеем права.
Теперь опять приводим полученную матрицу по строке и столбцу и вычисляем оценки qij.
Итак, нижняя оценка l (z) остается прежней: l 10(z)=8. Вычисляем оценки: q 13=0+1=1; q 14=0+0=0; q 35=3+1=4; q 42=2+1=3; q 54=1+0=1. Имеем: max q =4, то есть, выбираем c 35.
Склеиваем вершины 3 и 5, убирая из матрицы третью строку и пятый столбец, а обратный путь из 5 в 3 заменяем на ¥.
После приведения этой матрицы нижняя оценка веса цикла остается прежней. Вычисляем оценки qij: q 13=0+2=2; q 14=0+0=0; q 42=0+0=0. Выбираем c 13. Склеиваем вершины 1 и 3, удаляя первую строку и третий столбец. Получаем
Здесь уже без приведения ясно, что нужно брать (4,2) и (5,4).
Итак, мы получили следующий гамильтонов цикл: (3,5),(5,4),(4,2),(2,1),(1,3). Вес этого цикла равен l (z)=1+1+1+2+3=8, что удовлетворяет ранее найденной нижней оценке. Дерево решений для рассмотренного примера выглядит так, как показано на рис.3.28. В рассмотренном нами случае мы имели полный набор вариантов перехода, поэтому использовали только нижнюю оценку границы решений. Но если граф не полный, то, действуя по рассмотренной схеме, на каком-то шаге после приведения матрицы мы можем получить превышение нижней оценки веса цикла над L (z). В этом случае цикл, построенный для верхней оценки L (z), и будет искомым решением задачи.
27. Задача о раскраске графа. Понятие хроматического числа, его связь с валентностью вершин. Примеры графов с известным хроматическим числом. Теорема о раскраске планарных графов
В данной задаче страны можно представить вершинами графа, а отношение примыкания стран, то есть наличия у них общей границы, – ребрами (рис.3.30). Тогда задача ставится так: можно ли раскрасить вершины данного графа четырьмя красками, чтобы никакие две смежные вершины не были окрашены в один цвет. Более общая задача о раскраске графов: каким минимальным количеством красок можно раскрасить граф конкретного типа? В рассмотренной постановке – это задача о вершинной раскраске. Но поскольку задачу о реберной раскраске можно свести к задаче о вершинной раскраске так называемого смежностного графа, мы остановимся только на вершинной раскраске. Определение. Граф G называется k -раскрашиваемым, если существует разложение множества его вершин на k непересекающихся независимых множеств. Представление графа в таком виде называется k -раскраской. Из того, что это независимые множества вершин, следует, что все вершины каждого множества можно раскрасить в один цвет, и тогда никакие две вершины не будут раскрашены одинаково. Наименьшее число c =min(k) называется хроматическим числом графа G и обозначается c (G). Граф, имеющий хроматическое число c (G), называют c -хроматическим. Способ нахождения этого числа такой: выбираем из V макс. независимое множество S 1, затем из оставшихся вершин выбираем макс. независимое множество S 2 и так далее. Этот способ называют схемой Гранди. Задачи построения максимальных независимых множеств в общем случае решаются перебором. Тем не менее, зная свойства конкретного графа, перебор всегда можно сократить, а иногда и обойтись без него. Прежде всего, выделим некоторые виды графов с известным хроматическим числом. Граф, состоящий ровно из двух независимых множеств вершин, это двудольный граф(бихроматическим, так как его хроматическое число c =2.) Бихроматическими будут все известные нам виды графов, которые являются двудольными. Т.е. деревья и графы, в которых все циклы имеют четную длину. Отсюда для хроматического числа графа возникает ограничение снизу: если в графе G есть цикл нечетной длины, то его хроматическое число c (G)³3. Рассмотрим теперь раскраску полных графов. Для полного графа Kp c (G)= p, так как все вершины придется красить в разные цвета. Отсюда сразу следует ограничение сверху: для любого связного нетривиального графа c (G)£ d +1, где d – максимальная степень вершины графа. Из теоремы Эйлера о степенях вершин для графа с q ребрами получается следующая оценка
Теорема Брукса дает дополнительные условия для оценки c (G) сверху: если связный граф G не является ни полным графом, ни нечетным циклом, то c (G)£ d. Заметим, что в задаче о раскраске карт речь тоже идет об особом виде графов. Любой граф, описывающий на плоскости отношение смежности (примыкания), является планарным. Плоским или планарным называется граф, который можно разложить на плоскости без пересечения ребер. Теорема Понтрягина-Куратовского. Граф планарен, если он не содержит топологических миноров вида К 5 и R 6,3. Топологическим минором графа G называется граф G ’, который получается в результате склеивания некоторых смежных вершин из G. Для планарных графов доказано следующее ограничение по хроматическому числу. Теорема. Если граф G планарен, то c (G)£4. Заметим сразу, что это только достаточное условие. Иметь хроматическое число c (G)£4 могут и графы, не удовлетворяющие условию планарности. Начнем с того, что граф R 6,3 является двудольным, то есть бихроматическим. Но для графа К 5, как мы знаем, c (G)=5. Следовательно, высокое хроматическое число обусловлено присутствием в графе топологических миноров (или подграфов), являющихся полными графами. Поэтому более общие ограничения на c (G) дают следующие теоремы. Теорема. Если все конечные подграфы графа G k -раскрашиваемые, то граф G тоже k -раскрашиваемый. Теорема. Если граф G содержит полный подграф на m вершинах, то c (G)³ m. В качестве примера попробуем выполнить минимальную раскраску графа со следующим списком смежности: 1) 2,3,5,6,7,8; 2) 1,3,8; 3) 1,2,4,5,6,7; 4) 3,5,8; 5) 1,3,4,6,7; 6) 1,3,5,7; 7) 1,3,5,6,8; 8) 1,2,4,7. Сначала выполним оценку величины c (G), используя приведенные выше теоремы. Во-первых, данный граф заведомо не планарен, так как имеет более пяти вершин степени r ³4. Поскольку при стягивании ребра степень полученной вершины будет не меньше степеней инцидентных ему вершин, то в результате операций стягивания ребер мы обязательно получим топологический минор вида К 5. Следовательно, для нашего графа c (G)³5. И если нам удастся раскрасить граф в 5 цветов, значит, мы получили минимальную раскраску.
Тем не менее, все ребра, соединяющие вершины разных цветов, мы можем исключить из рассмотрения. В результате у нас остается подграф G ’ со следующим списком смежности: 2) 3,8; 3) 2,5,6,7; 5) 3,6,7; 6) 3,5,7; 7) 3,5,6,8; 8) 2,7. Построим и для этого подграфа остовное дерево, начиная с самой «тяжелой» вершины (рис.3.32).
Для вершин нечетных слоев (вершины 3 и 8) оставим цвет B, а для четного слоя (вершины 2, 5, 6, 7) введем новый цвет C. Если бы оставшиеся хорды подграфа соединяли только вершины разных цветов, процесс раскраски был бы завершен. Но наши хорды образуют треугольник (5, 6, 7) в пределах одного слоя. То есть три эти вершины должны быть окрашены в разные цвета. Поэтому оставляем для вершин (2, 5) цвет C, а для вершин 6 и 7 вводим цвета D и E соответственно. Итак, получаем раскраску из 5 цветов, которая соответствует нижней оценке хроматического числа c (G) для данного графа. Удаление любой из вершин 6 или 7 уменьшило бы хроматическое число графа. Графы, в которых удаление одной вершины приводит к уменьшению хроматического числа, называют критическими
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 697; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 Затем вычисляется некоторая оценка, которая служит критерием отсечения заведомо бесперспективных ветвей.
Затем вычисляется некоторая оценка, которая служит критерием отсечения заведомо бесперспективных ветвей.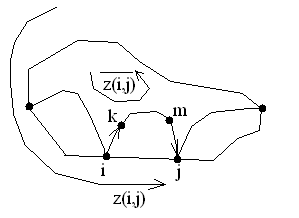

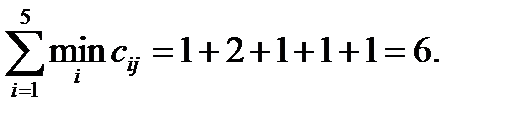


 соответственно. Они образуют две ветви решений.
соответственно. Они образуют две ветви решений. . Если путь не проходит через (i, j), то мы должны выйти из вершины i по какой-то дуге (i,k) и войти в вершину j по какой-то дуге (m,j). В наиболее удачном случае это будут дуги минимальных весов. Тогда
. Если путь не проходит через (i, j), то мы должны выйти из вершины i по какой-то дуге (i,k) и войти в вершину j по какой-то дуге (m,j). В наиболее удачном случае это будут дуги минимальных весов. Тогда