
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над множествами, их свойства. Связь с логическими законами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Операции над множествами. Операции над множествами подразумевают то или иное комбинирование элементов этих множеств. Поэтому операции можно выполнять только над множествами объектов, которые принадлежат одному и тому же универсуму: AÌ U, BÌ U. На конечном универсуме U, состоящем из элементов x, мы можем создать 2| U | различных множеств, включая сам универсум и пустое множество Æ. Объединение множеств AÈB есть множество элементов x, принадлежащих либо A, либо B: AÈB={ x | x ÎAÚ x ÎB}. Пересечение множеств AÇB есть множество элементов x, принадлежащих одновременно A и B: AÇB={ x | x ÎA& x ÎB}. Разность множеств A\B есть множество элементов x, принадлежащих A, но не принадлежащих B: A\B={ x | x ÎA& x ÏB}. Симметрическая разность множеств ADB есть множество элементов x, принадлежащих либо A, либо B, но не принадлежащих A и B одновременно: ADB= (AÈB)\(AÇB)={ x |(x ÎA& x ÏBÚ x ÎB& x ÏA}. Дополнением множества A называется множество Любой последовательности операций над множествами можно сопоставить логическую формулу, где логическими переменными являются предикаты принадлежности элементов множествам. Этот способ выполнения операций над множествами иногда называют методом характеристических функций [2]. Связь с логическими операциями. AÈB={ x | x ÎAÚ x ÎB}={ x | a Ú b } Û дизъюнкция: a Ú b. AÇB={ x | x ÎA& x ÎB}={ x | a & b } Û конъюнкция a × b. A\B={ x | x ÎA& x ÏB}= ADB= (AÈB)\(AÇB)={ x |(x ÎA& x ÏBÚ x ÎB& x ÏA}=
Свойства операций над множествами. Введем обозначения: a =«x ÎA», b =«x ÎB» и рассмотрим последовательно все логические законы. 1. Закон отрицания отрицания: 2. Коммутативность, ассоциативность и дистрибутивность операций над множествами вытекают из соображения, что предикаты принадлежности, через которые мы определяем эти операции, не задают никакого правила расположения элементов внутри самих множеств. Следовательно, «x ÎAÚ x ÎB»Û«x ÎBÚ x ÎA» Þ AÈB=BÈA (коммутативность объединения). Аналогичные рассуждения можно провести и для двух других операций. 3. Закон нуля и единицы: 4. Законы де Моргана. Покажем, что 5. Законы поглощения. A È(A Ç B)={ x | x Î A Ú(x Î A & x Î B)}, а поскольку Q ={ x | x Î A & x Î B }ÌA, то множество A можно рассматривать по отношению к Q как универсум. Используя закон нуля и единицы, имеем: A È Q = A. Следовательно, A È(A Ç B)= A. Аналогично можно получить, что A Ç(A È B)= A. 6. Законы склеивания. Пример 1. Найти результат следующих операций над множествами A,B,C: Q =((A D B)È(B Ç C))\(A Ç C). Введем обозначения: a =«x Î A», b =«x Î B», с =«x ÎС» и запишем данное выражение в предикатной форме: Q ={ x |((a Å b)Ú b × c)- a × c }. Выполним преобразования над логическим условием, используя представление логических операций через ДНФ и логические законы: Пример 2. Показать, что ((B D C)\ A)Ç(A D C)Ì С. Выполним операции над множествами через преобразование соответствующего этим операциям логического выражения:
Отсюда имеем, что
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 ={ x|x Ï A }. Дополнение рассматривается относительно универсума:
={ x|x Ï A }. Дополнение рассматривается относительно универсума: 
 Û разность:
Û разность: 
 сложение по модулю 2:
сложение по модулю 2: 
 Û отрицание:
Û отрицание:  .
. . Согласно нашим обозначениям,
. Согласно нашим обозначениям,  - дополнение множества A до универсума:
- дополнение множества A до универсума:  . Тогда
. Тогда 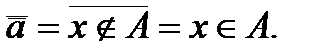 Отсюда
Отсюда  . Это свойство операции над множествами иногда называют инволютивностью [1].
. Это свойство операции над множествами иногда называют инволютивностью [1]. ={ x | x Î A & x Ï A }={ x |
={ x | x Î A & x Ï A }={ x |  }=Æ, поскольку выражение
}=Æ, поскольку выражение  является противоречием.
является противоречием.  ={ x | x Î A Ú x Ï A }={ x |
={ x | x Î A Ú x Ï A }={ x | 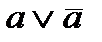 }= U, поскольку
}= U, поскольку  - тождество. A Ç U = U, A È U = U, так как A Ì U.
- тождество. A Ç U = U, A È U = U, так как A Ì U.  , так как
, так как  . Пусть Q={ x | x Î
. Пусть Q={ x | x Î  }. Это означает, что x ÏAÇB. Значит, либо x Ï A, либо x Ï B. Перейдем к записи этого условия через предикаты принадлежности и получим:
}. Это означает, что x ÏAÇB. Значит, либо x Ï A, либо x Ï B. Перейдем к записи этого условия через предикаты принадлежности и получим:  С другой стороны, в соответствии с записью операции пересечения через предикаты принадлежности, имеем:
С другой стороны, в соответствии с записью операции пересечения через предикаты принадлежности, имеем:  То есть
То есть  , откуда и получаем
, откуда и получаем  .
. . Воспользуемся дистрибутивным законом:
. Воспользуемся дистрибутивным законом: 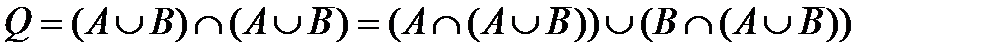 . Применив к левой скобке в операции объединения закон поглощения, а к правой – еще раз дистрибутивный закон, а затем закон нуля и единицы, имеем:
. Применив к левой скобке в операции объединения закон поглощения, а к правой – еще раз дистрибутивный закон, а затем закон нуля и единицы, имеем:  . Еще раз применяем закон поглощения и получаем Q = A. В качестве упражнения, покажите самостоятельно, что
. Еще раз применяем закон поглощения и получаем Q = A. В качестве упражнения, покажите самостоятельно, что  .
. После преобразования получаем:
После преобразования получаем:  .
.

 , то есть Q является подмножеством C.
, то есть Q является подмножеством C.


