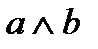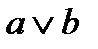Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие логического высказывания. Элементарное и сложное высказывание. Логические выражения (формулы) и логические операции. Диаграммы Венна.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Описание числовых множеств на плоскости.диаграммы Эйлера. Диаграммы Эйлера – это графический способ представления операций над множествами, который появился раньше диаграмм Венна (Эйлер жил в XVIII веке, а математическая логика как наука сформировалась значительно позже). Рассмотрим в качестве универсума множество всех точек плоскости. Введем декартову систему координат (X, Y).Если объект линейный, то множество описывается функцией y = f (x). Если объект площадной (полигон), то он описывается системой неравенств (предикатов) вида y>f(x), y³ f(x) (если граница включается) или y<f(x). Знак неравенства зависит от того, с какой стороны от ограничивающей функции лежат принадлежащие полигону точки. Например, множество точек, принадлежащих кругу A с центром в точке (a,b) и радиусом r, описывается неравенством (x-a)2+(y-b)2£r2. Выполнение этого неравенства для некоторой точки (x, y) соответствует значению «true» предиката принадлежности «(x, y)ÎA». 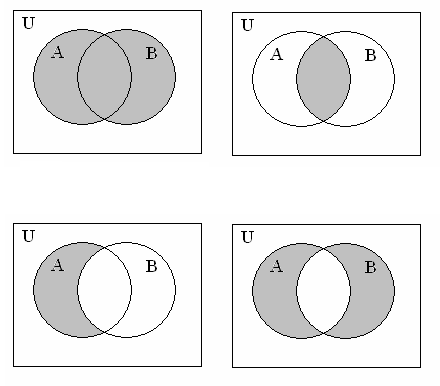
Семейство подмножеств E={Ei},i=1,…,|E | называется покрытием множества M, если каждый элемент из M принадлежит хотя бы одному Ei. Семейство называется дизъюнктным или, иначе, разбиением M, если каждый элемент M принадлежит только одному Ei. Пример 1. Описать заштрихованные части фигуры как операции над множествами точек плоскости.
A ={(x, y)| | x |+| y |£3}, B ={(x, y)| |3 x |+| y |£3, C ={(x, y)| | x |+|3 y |£3}. При таком задании множеств-операндов незаштрихованную часть фигуры можно описать как (B È C)\(B Ç C), то есть как симметрическую разность B D C. Следовательно, заштрихованную часть Q данной фигуры наиболее коротким способом можно представить как Q = A \(B D C). Ответ: Q = A \(B D C), где A ={(x, y)| | x |+| y |£3}, B ={(x, y)| |3 x |+| y |£3, C ={(x, y)| | x |+|3 y |£3}.
Подграфы и части. Операции над графами. Подграфы. Основные определения. Граф G ’ называется подграфом графа G, если V ’Ì V и E ’Ì E. Если в графе G ’ нет изолированных вершин, можно ограничиться только условием E ’Ì E.
Граф G ’ называется остовным подграфом графа G, если V ’= V. Ясно, Нуль-граф { V ’= V, E ’=0} тоже является остовным подграфом G. Граф G ’ называется индуцированным подграфом на графе G, если " v iÎ V ’, v jÎ V ’ (v i, v j)Î E Þ(v i, v j)Î E ’. Ясно, что если остовный подграф одновременно является индуцированным, то он совпадает с самим графом G.
Операции над графами. Поскольку граф - это однородное бинарное отношение на V2, то, казалось бы, операции над графами будут те же самые, что и для отношений. Давайте посмотрим, что происходит на самом деле. Во-первых, чтобы выполнять некоторые операции, нам нужно ввести понятие «универсума». Если мы примем за универсум полный неориентированный граф на p вершинах, то относительно операций над ребрами, то есть на множестве E, мы можем построить булеву алгебру (вспомним представление графов матрицей смежности). Минимальным элементом у нас тогда будет нуль-граф, максимальным – полный неориентированный граф, и можете сами проверить, что все законы логики (то есть соответствующие им свойства операций над множествами ребер) будут выполняться. Но поскольку граф, по определению, - конструкция из двух множеств, операции над графами рассматриваются не только как операции на множестве ребер, но и как операции на множестве вершин. Начнем с операций добавления и удаления элементов графа. Удаление ребра e приводит к образованию графа G ’, где V ’= V & E ’= E \{ e }. Ясно, что добавление ребра образует граф G ’, где V ’= V & E ’= E È{ e }. То есть множество–носитель отношения не меняется. А что же происходит при операциях с вершинами? Удаление вершины v приводит к образованию графа G ’, где V ’= V \{ v } & E ’= E \{ e i | e i=(v i, v) Ú e i=(v, v i)}. Но здесь заметим, что для полных графов K 3\{ v }= K 2, K 4\{ v }= K 3,…, K n\{ v }= K n-1, n =| V | (попробуйте сами объяснить, почему). Посмотрим теперь, как добавлять элементы графа. Здесь тоже есть нюанс. Просто добавление вершины v – это расширение множества V: V ’= V È{ v }. Но есть еще операция стягивания графа G к вершине v. В результате этой операции образуется граф G ’, где V ’= V È{ v } & E ’= E È{ e =(v, v i), i=1,…,| V |}. Таким образом, для полного графа операция стягивания является обратной к операции удаления вершины. Но только для полного графа. Теперь перейдем от операций с элементами графа к операциям над графами в целом. Просто под дополнением Объединением графов G 1È G 2 при V 1Ç V 2=Æ называется граф G ’, где V ’= V 1È V 2 & E ’= E 1È E 2. В случае V 1Ç V 2=Æ операцию объединения графов называют прямой суммой. В принципе, операцию объединения нетрудно распространить и на случай V 1Ç V 2¹Æ, обозначив V 3= V 1Ç V 2. Тогда мы получаем, что V ’= V 3È(V 1- V 3)È(V 2- V 3), где (V 1- V 3)Ç(V 2- V 3)=Æ. На V 3 мы выполняем объединение как операцию над бинарными отношениями, а на (V 1- V 3)Ç(V 2- V 3) - по правилу объединения графов. Заметим, что в данном случае мы рассматривали графы с фиксированной нумерацией вершин, то есть без учета изоморфизма. Но свойства графов, в том числе и свойства операций, мы обязаны рассматривать для всего класса изоморфных графов и тогда должны предполагать, что V 1Ç V 2=Æ. Соединением графов G 1+ G 2 при V 1Ç V 2=Æ называется граф G ’, где V ’= V 1È V 2 & E ’= E 1È E 2.{ e ij=(v i, v j), i=1,…, p 1, j=1,…, p 2}.
Заметим, что в результате соединения полных графов мы опять получаем полный граф. А вот в результате соединения двух нуль-графов мы получаем очень интересную конструкцию, которая называется двудольным графом. Причем не просто двудольным, а так называемым полным двудольным графом. Такие графы обозначают Km,n, где m = p 1, n = p 2.
14. Маршруты, цепи, циклы. Понятие связности и достижимости. Взаимосвязь числа компонент связности с основными инвариантами графа. Графы и бинарные отношения. Транзитивное замыкание. Маршрутом в графе называется любая последовательность попарно смежных (в орграфе – непосредственно достижимых) вершин { v 0, v 1,…, v k}. В маршруте как вершины, так и ребра могут повторяться. Если v 0 = v k, то маршрут называется замкнутым, в противном случае – открытым. Если в маршруте каждое ребро встречается ровно один раз, то такой маршрут называется цепью. Если при этом в цепи каждая вершина встречается только один раз, то такая цепь называется простой цепью. Замкнутая цепь называется циклом (в орграфе – контуром), соответственно, замкнутая простая цепь называется простым циклом. Чтобы решать любые задачи обхода графа, необходимо ввести понятие связности. Связным называется граф, любые две вершины которого соединены простой цепью. При большом количестве ребер таких цепей можно построить много. Какие-то из них будут короче, какие-то длиннее. Самая короткая из цепей, соединяющих две вершины графа, называется геодезической, а ее длина – расстоянием между вершинами. Самая длинная геодезическая называется диаметром графа. Для ориентированных графов понятие цепи, следовательно, и понятие связности можно ввести только при снятии ориентации ребер. Если же учитывать ориентацию, то мы обязаны будем ввести какие-то дополнительные понятия. В этом случае нам придется рассматривать не цепи, а пути. Путем в орграфе называется последовательность вершин, непосредственно достижимых одна из другой. Замкнутый путь называется контуром. Покажем, что связность есть отношение эквивалентности. Связность рассматривается как достижимость одной вершины из другой при отсутствии ориентации ребер, то есть (u, v)=(v, u) " u, v Î V. Топологическим минором графа G называется граф G ’, который получается в результате склеивания некоторых смежных вершин из G. Операция склеивания вершин vi и vj называется еще стягиванием ребра e =(vi, vj). При стягивании ребра (vi, vj) все отношения смежности, которые были у вершин vi и vj, переходят к новой вершине v (рис.3.6). Но при этом если для какой-то вершины v k существовала пара ребер (vi, vk) и (vj, vk), то эта пара превращается в одно ребро (v, vk).
Ясно, что если мы стягиваем неориентированное ребро, то мы не теряем никакой информации о связности вершин графа, поскольку можем пройти по ребру в любом направлении. А вот если мы стянем ориентированное ребро, то здесь мы можем либо потерять некоторые пути, либо получить лишние. Поэтому говорить про достижимость вершины самой из себя на орграфе некорректно. Под рефлексивностью тогда следует понимать возможность опять вернуться в эту вершину после выхода из нее. Т.е. в графе должен существовать замкнутый контур, включающий эту вершину. Кстати, в этом случае мы, возможно, кое-что сможем и склеить без потери информации. Свойства отношения «связность». Рефлексивность. Если граф неориентированный, то, выйдя из какой-то вершины, мы всегда можем вернуться в нее назад, поскольку можем двигаться по ребру в любом направлении. Симметричность. Если из vi можно попасть в vj, то по любой из цепей, соединяющих vi и vj, можно попасть обратно. Транзитивность. Если из vi можно пройти в vj, а из vj в vk, то через vj можно пройти из vi в vk. Если граф связен, то мы можем обойти его за один проход, но только если он неориентированный. Для ориентированных графов дело обстоит сложнее. Именно для них и возникает понятие достижимости, поскольку мы будем двигаться только по исходящим дугам и в какой-то момент можем оказаться в вершине, у которой таковых нет. Орграф Gd называется связным, если связен граф, который получается из Gd при снятии с ребер ориентации. То есть если между каждой парой вершин существует либо путь S (v i, v j), либо путь S (v j, v i). Посмотрим теперь, какому типу отношения соответствует понятие достижимости. Легко проверить, что будет выполняться транзитивность. Если граф строго ориентированный, а не смешанный, то отношение будет антисимметрично. Т.е. отношение частичного порядка мы уже получили. Теперь - рефлексивность. Рефлексивностью - возможность возвращения в вершину по какому-то маршруту. В случае ориентированного графа это получается замкнутый путь - контур. То есть если в ориентированном графе существуют контуры, это уже отношение нестрогого частичного порядка, а отношению строгого частичного порядка будет соответствовать бесконтурный ориентированный граф. Матрица достижимости и транзитивное замыкание. Матрицей достижимости называется матрица M размерности p ´ p, где mij =1, если vi достижима из vj, и mij =0 в противном случае. Для связного неориентированного графа такая матрица будет состоять из одних единиц. Причем по диагонали тоже будут стоять единицы, потому что, походив-походив по графу, мы всегда можем вернуться назад, хотя бы тем же самым путем (не так, как в задаче о 7 мостах). А вот для ориентированного графа матрица M будет другой. И по ее виду мы можем понять, какой тип отношения порядка задает граф Gd. Если по диагонали будут одни нули, значит, это отношение строгого частичного порядка, поскольку имеет место антирефлексивность. В противном случае мы имеем отношение нестрогого частичного порядка. Определяя транзитивность, мы писали такое выражение R o R Ì R. То есть отношение транзитивно, если оно замкнуто относительно операции композиции. R образует полугруппу относительно операции композиции. Если отношение задано бинарной матрицей A размерности n ´ n, то операция композиции есть логическое произведение A × A. A × A для матриц непосредственной достижимости- это матрица путей, состоящих из двух ребер, то есть матрица достижимости одной вершины из другой за два шага. Тогда A × A × A есть матрица достижимости одной вершины из другой за три шага, и так далее. Ясно, что таких шагов t будет не более чем p -1, причем t = p -1, только если диаметр графа есть p -1. Значит, в общем случае, чтобы получить полную матрицу достижимости, мы должны объединить все пути длиной от 1 до p -1 ребра. Итак, имеем: Вспомним что такое замыкание отношения относительно некоторого свойства (Пусть R и R’ – однородные отношения на множестве A. Отношение R’ называется замыканием отношения R относительно свойства C, если 1) R’ обладает свойством C; 2) R является подмножеством R’: RÌR’; 3) R является наименьшим среди всех R’’, таких что имеет место C(R’’) и RÌ R’’.) и обратим внимание, что здесь мы как раз и имеем случай такого замыкания. Матрица M объединяет все варианты путей - отношений достижимости между парами вершин, то есть является надмножеством над всеми возможными путями - отношениями. При этом она не включает ничего лишнего, только простые цепи. То есть это минимальное надмножество, обладающее свойством транзитивности. Поэтому матрицу M называют иначе транзитивным замыканием отношения достижимости. Подмножества вершин графа, образующие классы эквивалентности относительно отношения связности, называются компонентами связности или связными компонентами (рис.3.7).
К аждый граф единственным способом представим в виде прямой суммы своих связных компонент. Для графа, состоящего из нескольких связных компонент, матрица достижимости будет состоять не только из одних единиц. Используя понятие изоморфизма, мы можем перестановкой строк и столбцов привести ее к блочно-диагональному виду и определить, сколько в нашей конструкции связных компонент, а также размеры этих компонент. Каждой компоненте будет соответствовать определенный блок из единиц вдоль диагонали. Число компонент связности k является инвариантом графа, так же, как число вершин p и число ребер q. Если k =1, то мы имеем просто связный граф. Для решения некоторых задач, например, для построения топологической модели очень большой сети, важно заранее знать, будет ли данный граф связным. Или же сделать приблизительную оценку числа компонент связности, без построения матрицы достижимости и приведения ее к блочно-диагональному виду. Для этого можно использовать следующее отношение между основными инвариантами графа. Теорема. Пусть p – число вершин, q – число ребер, k - число компонент связности графа. Тогда
Докажем левую часть отношения. Для того чтобы соединить p точек, нужно, по меньшей мере, p -1 ребро, то есть q ³ p-1. Если в графе k компонент связности, каждая из которых содержит p i вершин (i=1,…, k), то, просуммировав неравенства для ребер по всем k компонентам, получаем искомую нижнюю оценку. Правую часть отношения докажем, используя, наоборот, полные графы, в которых число ребер максимально. Самое большое число ребер в графе, состоящем из k компонент связности, будет в том случае, когда он представляет собой прямую сумму полных графов. Полный граф, в свою очередь, имеет Теперь осталось выяснить, при каком числе k общее число ребер будет максимально. В результате операции соединения двух полных графов у нас опять получается полный граф. Такое соединение добавляет D q = p 1× p 2/2 ребер. Общее число ребер в двух соединяемых связных графах равно q =1/2[(p 1+ p 2)(p 1+ p 2-1)- p 1× p 2], следовательно, q будет тем больше, чем меньше величина D q = p 1× p 2/2 - число добавляемых ребер. Минимальное же количество ребер добавляется при добавлении одной вершины: p 2=1, D q=p 1 - 1. То есть максимальное количество ребер в графе из k компонент будет тогда, когда одна компонента – полный граф, а остальные – изолированные вершины. Число ребер в таком графе q =(p - k)(p - k +1)/2. Отсюда имеем искомое неравенство. Следствие. Если q >(p -1)(p -2)/2, то граф связен.
Теорема Менгера. рассмотрим задачу. Менеджер фирмы, находящейся в городе A, собирается лететь на деловые переговоры в город F, с которым нет прямого воздушного сообщения. Учитывая плохие погодные условия, менеджер выписал для себя все возможные варианты перелетов с пересадками в городах В, С, D, E, G, H, K, L, M, в результате чего получился граф, представленный следующими списками смежности. А: B,C,G,K,M; B: C,H; C: E,G,M; D: F,H,M; E: C,F,L; F: D,E,H,L,M; G: A,C,L; H: B,D,F,K; K: A,H,L; L: E,F,G,K; M: A,D,F. Попадет ли менеджер на переговоры, если перед его вылетом в трех городах из списка все рейсы были отменены по погодным условиям? Поставленное условие означает, что закрытые аэропорты – это вершины, удаление которых разбивает граф на две компоненты связности, причем пункты вылета и назначения находятся в разных компонентах. Нужно ли для решения этой задачи тупо перебирать все возможные варианты перелета? Вот на этот вопрос, собственно, и отвечает теорема Менгера. Но прежде чем ее сформулировать, нам придется ввести еще несколько определений. Определение. Пусть u,v – две несмежные вершины связного графа G (V, E). Две цепи S 1(u, v), S 2(u, v) называются вершинно непересекающимися, если они у них нет общих вершин, кроме u и v. Соответственно, цепи S 1(u,v), S 2(u,v) называются реберно непересекающимися, если у них нет общих ребер. Говорят, что множество G ’(u,v)Ì G разделяет две вершины u,v, если эти вершины принадлежат разным компонентам связности G 1Ì G, G 2Ì G, где G 1È G 2È G ’= G. Здесь, как и раньше, следует выделить два вида разделяющих множеств. Определение. Разделяющим множеством вершин для пары u, v называется множество R (u,v)Ì V, такое, что u Î G 1, vÎ G 2, V 1È V 2È R = V, E 1È E 2È E ’= E, где E ’= E \(E 1È E 2). Соответственно, разделяющим множеством ребер называется P (u, v), такое, что u Î G 1, v Î G 2, V 1È V 2= V, E 1È E 2È E ’= E, где E ’= E \(E 1È E 2). Разделяющее множество ребер обычно называют разрезом. Теорему Менгера сформулируем без доказательства, его можно посмотреть, например, в [1]. Эта теорема может быть сформулирована как в вершинной, так и в реберной форме. Теорема Менгера в вершинной форме. Мощность наименьшего разделяющего множества вершин R (u, v) для пары вершин u и v равна максимальному количеству вершинно непересекающихся простых цепей S (u,v): min| R (u,v)|=max | S v(u,v)|. Теорема Менгера в реберной форме. Мощность наименьшего разреза P (u,v) для пары вершин u и v равна максимальному количеству реберно непересекающихся простых цепей S (u,v): min| P (u,v)|=max | S e(u,v)|. Поскольку мы уже видели, что вершинная связность понятие более «сильное», теорему Менгера чаще используют в вершинной форме. Однако реберная форма теоремы Менгера тоже имеет практическое значение. Итак, для решения задачи про аэропорты нам не нужно перебирать все возможные варианты перелета. Достаточно найти максимальное количество вершинно непересекающихся простых цепей между пунктами A и F. Давайте попробуем это сделать. Во-первых, заметим, что количество таких цепей не может быть больше, чем число вершин, смежных с вершиной A, и не может быть больше, чем число вершин, смежных с вершиной F. В противном случае цепи неизбежно будут пересекаться по вершинам. Итак, | S |<min(r(A),r(F))=5, и в данном случае обе эти вершины имеют максимальную степень. Для дальнейшего анализа можно воспользоваться схемой поиска в ширину, начиная с концевой вершины маршрута, имеющей минимальную степень. Для нашего случая схема поиска в ширину будет иметь следующий вид (рис.3.11). В этой схеме уже имеется одна простая цепь (A,M,F). Еще три цепи получаем непосредственным переходом в F из смежных с ней вершин H,E,L. Из вершины К мы не можем непосредственно попасть в F, а все остальные вершины уже задействованы в цепях. Таким образом, в рассматриваемом графе существует 4 вершинно непересекающихся простых цепи. И этого достаточно, чтобы менеджер смог добраться на переговоры, так как при любых трех закрытых аэропортах у него всегда останется один запасной вариант.
26. Независимые и покрывающие множества вершин и ребер. Теорема Галаи. Мы уже рассматривали некоторые задачи о покрытиях. Например, говорили о том, как покрыть граф минимальным числом простых цепей, и это была задача на построение эйлерова цикла в дополненном фиктивными ребрами графе. Теперь мы рассмотрим задачу, как описать граф минимальным количеством вершин, чтобы сохранились все связи. Это может быть, например, задача оптимизации сетевой базы данных. Другим примером практической задачи может быть задача о расположении ретрансляторов в телекоммуникационных сетях. Задачи такого типа часто иллюстрируют головоломкой о том, как расставить на шахматной доске заданное количество фигур, чтобы они били все клетки. Мы знаем, что при удалении вершины из графа вместе с ней уходят и все инцидентные ей ребра. Будем поэтому говорить, что вершина покрывает эти ребра. И, соответственно, будем говорить, что ребро ( i,j ) покрывает вершины i,j, если эти вершины являются его концами. Определение. Множество вершин, покрывающее все ребра графа G, называется вершинным покрытием графа G. Аналогично, множество ребер, покрывающих все вершины графа G, называется реберным покрытием G.
Похоже, что для каждого графа с определенными особенностями связей существует какое-то минимальное покрытие, как вершинное, так и реберное, и мощность этого минимального покрытия также является числовой характеристикой - инвариантом для всего класса изоморфных графов. Давайте выясним этот вопрос. Введем обозначения: a0 – мощность минимального вершинного покрытия (число вершинного покрытия), a1 – мощность минимального реберного покрытия (число реберного покрытия). Теперь вернемся к примеру со звездой (рис. 3.29), как к критическому случаю. Обратите внимание, что здесь покрывающее множество состоит из одной вершины именно потому, что между другими вершинами нет ребер. Если бы было хотя бы одно такое ребро, было бы другое минимальное покрывающее множество. Чтобы сделать какие-то выводы относительно такой ситуации, введем еще одно понятие. Множество вершин называется независимым, если никакие две вершины в нем не смежны. Соответственно, множество ребер называется независимым, если в нем никакие два ребра не имеют общего конца. Мощность максимального независимого множества вершин в графе называется вершинным числом независимости и обозначается b0. Мощность максимального независимого множества ребер называется реберным числом независимости и обозначается b1. С такими конструкциями мы, на самом деле, уже сталкивались, когда говорили о двудольных графах. В двудольном графе каждая из долей представляет собой независимое множество вершин. А независимое множество ребер, в свою очередь, является паросочетанием. Так вот, оказывается, что минимальные покрывающие множества и независимые множества вершин и ребер связаны между собой следующей зависимостью. Теорема Галаи. Для любого нетривиального связного графа справедливо следующее соотношение a0+b0=a1+b1=p. Понятие логического высказывания. Элементарное и сложное высказывание. Логические выражения (формулы) и логические операции. Диаграммы Венна. Высказывание- повествовательное предложение (утверждение), которое может быть либо истинным, либо ложным, но не то и другое вместе. Заключение, которое мы делаем относительно того, истинно или ложно высказывание, называется его истинностным значением. Для истинностных значений высказываний используются обозначения И (истина), Л (ложь); в компьютерных приложениях и языках программирования используются обозначения true, false или, соответственно, «1», «0». Элементарное (простое) -высказывание, которое нельзя разбить на более простые без потери смысла, следовательно, истинностного значения. Если же высказывание расчленяется на составляющие, которые также имеют смысл и, следовательно, истинностное значение, оно называется сложным. Такое высказывание будет истинным или ложным в зависимости от значений входящих в него элементарных высказываний. В математической логике элементарные высказывания называют логическими переменными. Логические переменные обычно обозначают прописными латинскими буквами: a,b,c,… Связки, образующие сложное высказывание, называются позиционными связками или логическими операциями. Сложные высказывания, записанные с помощью логических переменных и операций, называют логическими выражениями или логическими формулами. Значения, которые принимают логические выражения в зависимости от значений логических переменных, можно представить в табличной и графической форме. Табличную форму представления называют таблицами истинности. Каждая строка таблицы содержит упорядоченный набор значений всех переменных и соответствующее ему значение функции.
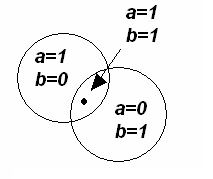
С помощью n двоичных разрядов можно представить 2n различных чисел. Следовательно, для n логических переменных таких наборов будет 2n. Графическим способом представления сложных высказываний через элементарные являются диаграммы Венна. В диаграмме Венна каждому элементарному высказыванию сопоставляется замкнутый контур (рис.1.1). Внутри этого контура высказывание считается истинным, за пределами контура – ложным. Контуры для n элементарных высказываний, входящих в сложное, изображаются так, чтобы все их возможные перекрытия давали полный набор всех возможных комбинаций значений элементарных высказываний, то есть 2n. На плоскости таким способом можно наглядно отобразить значения логических формул только от трех переменных. (Для четырех простых контуров мы уже никак не получим ровно 24 областей)
Если сложное высказывание истинно при нулевых значениях всех переменных, точка ставится за пределами всех контуров. Логические операции. Самой простой логической операцией является отрицание того утверждения, которому соответствует элементарное высказывание. Отрицание обозначается символами Поскольку операция отрицания применяется только к одной переменной, она называется одноместной или унарной. Если a= 1, то Ø a= 0 и, наоборот, если a= 0, то Ø a= 1. Простейшие из сложных высказываний, соответствующие привычным для нас конструкциям речи, описываются операциями с двумя переменными. Они называются двухместными или бинарными. Основными бинарными операциями принято считать следующие. 1. Конъюнкция (логическое умножение). Соответствует речевой связке «и». В математической логике связка «и» означает только одновременное выполнение каких-либо условий или одновременное осуществление каких-либо событий. Конъюнкция обозначается a×b, a & b, a Ù b. Таблица истинности для конъюнкции.Диаграмма Венна
Поскольку конъюнкция принимает значение 1 только при a = b =1, в двоичной системе счисления эту операцию можно рассматривать как min(a,b). 2. Дизъюнкция (логическое сложение). Соответствует связке «или» и обозначает объединение каких-либо условий или событий. Т.е. сложное высказывание является истинным, когда истинно хотя бы одно из элементарных высказываний. Дизъюнкция обозначается a Ú b. Таблица истинности для дизъюнкции. Диаграмма Венна
для дизъюнкции.
Поскольку дизъюнкция принимает значение 0 только при a = b =0, в двоичной системе счисления эту операцию можно рассматривать как max(a,b). 3. Импликация (следование, достаточное условие в доказательствах теорем). Соответствует связке «если …, то …». Обозначается a ® b. Определение значений импликации в зависимости от значений a и b основывается на следующем соображении. Из ложной посылки может следовать как истина, так и ложь. Но из истины всегда следует только истина. Поэтому импликация принимает значе
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 905; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.132.80 (0.014 с.) |

 Чтобы получить наиболее рациональное описание множеств, заметим, что ромб с вершинами в точках (3,0), (0,3), (-3,0), (0,-3) может быть аналитически описан уравнением | x| +| y |=3. Его внутренняя часть (с границей) определяется неравенством | x |+| y |£3. Соответственно, внутреннюю часть ромба с вершинами (1,0), (0,3), (-1,0), (0,-3) можно задать как |3 x |+| y |£3, а ромба с вершинами (3,0), (0,1), (-3,0), (0,-1) – как | x |+|3 y |£3. Три ромба, составляющие рассматриваемую фигуру, можно описать как множества:
Чтобы получить наиболее рациональное описание множеств, заметим, что ромб с вершинами в точках (3,0), (0,3), (-3,0), (0,-3) может быть аналитически описан уравнением | x| +| y |=3. Его внутренняя часть (с границей) определяется неравенством | x |+| y |£3. Соответственно, внутреннюю часть ромба с вершинами (1,0), (0,3), (-1,0), (0,-3) можно задать как |3 x |+| y |£3, а ромба с вершинами (3,0), (0,1), (-3,0), (0,-1) – как | x |+|3 y |£3. Три ромба, составляющие рассматриваемую фигуру, можно описать как множества: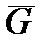 графа G подразумевается дополнение его до полного графа Kp, где p =|V|. Употребляется также дополнение графа G ’ до графа G. Его обозначают G - G ’. Точно так же, как мы определяли дополнение бинарного отношения. А вот с другими операциями дело обстоит иначе.
графа G подразумевается дополнение его до полного графа Kp, где p =|V|. Употребляется также дополнение графа G ’ до графа G. Его обозначают G - G ’. Точно так же, как мы определяли дополнение бинарного отношения. А вот с другими операциями дело обстоит иначе.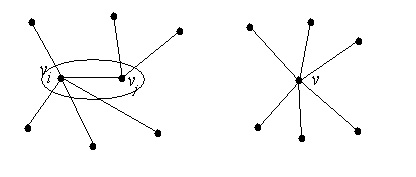
 .
.
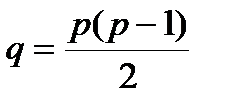 ребер.
ребер.