
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы цикломатики. Фундаментальная система циклов, цикломатическое и коциклическое число.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Циркуляция по контуру не увеличивает поток от источника к стоку. Т.е.можно всегда построить бесконтурную сеть с таким же потоком, как и в исходной сети с контурами. Встает вопрос: а сколько ребер нужно убрать из графа, чтобы в нем не осталось циклов? Из подобных задач возникают такие понятия, как фундаментальная система циклов и фундаментальная система разрезов. Рассмотрим произвольное остовное дерево графа G (V, E). Если добавить в дерево ровно одно ребро, мы получим ровно один цикл. Но если мы добавим сразу два ребра, то мы можем получить уже больше циклов, но часть этих циклов будут производными от тех, которые получаются в результате добавления каждого из этих ребер отдельно (рис.3.23). Поэтому фундаментальными называют циклы, которые образуются в результате добавления каждого из ребер, входящих в дополнение остовного дерева G ’(V ’, E ’) до исходного графа G. Эти ребра называют хордами.
Мы знаем, что остовное дерево графа содержит ровно p -1 ребро. Если всего в графе q ребер, то хорд будет q-p +1. Т.о., число фундаментальных циклов равно числу хорд в графе G: m (G)= q-p +1. Эта величина тоже является одним из инвариантов графа и называется цикломатическим числом. Каждое ребро в остовном дереве является мостом, то есть разрезом. Поэтому остовное дерево иначе называют фундаментальной системой разрезов или коциклов, а величину p- 1 называют коциклическим или коцикломатическим числомграфа. С каждой фундаментальной системой разрезов связана определенная фундаментальная система циклов.
13.Понятие изоморфизма графов. Основные инварианты графа. Теорема Эйлера о степенях вершин. Подграфы и операции над графами. Графы G и G ’ изоморфны, если один получается из другого перенумерацией вершин. Если рассмотреть матрицы смежности этих графов, то для получения A ’ из A нужно поменять местами соответствующие строки и столбцы матрицы A. То есть для компьютерной программы изоморфизм отнюдь не очевиден, и поиск изоморфных графов представляет собой задачу перебора, как, кстати, и многие другие задачи теории графов. Хотя перебор во многих случаях может быть существенно сокращен за счет использования каких-то свойств анализируемых графов.
Математически изоморфизм определяют как биекцию V ® V ’, сохраняющую смежность, или, если каждой вершине из V инцидентно хотя бы одно ребро, биекцию E ® E ’. Вот, кстати, повод вспомнить, что такое биекция. Прежде всего, это функциональное отношение или просто функция. То есть для каждого прообраза e =(v i, v j) существует единственный образ e ’=(v ’i, v ’j). Эта функция тотальна и сюръективна, поскольку V = V ’. А поскольку каждому ребру e ’ соответствует только одно ребро e, то данная функция инъективна. Таким образом, мы имеет тотальную инъективную и сюръективную функцию, то есть биекцию. Рассмотрим свойства этого биективного функционального отношения. Прежде всего, заметим, что оно однородно, поскольку определено на множестве { G }´{ G }. Рефлексивность. Отношение двух одинаковых графов с одинаковой нумерацией вершин есть тождественное отношение. Следовательно, наша биекция рефлексивна. Симметричность. Если два графа отличаются только порядком нумерации вершин, то мы можем как первый получить из второго, так и второй получить из первого обратной перенумерацией вершин. Значит, отношение симметрично. Транзитивность. Если мы можем получить G2 из G1, заменив каждый номер i1 на номер i2, а G3 получить из G2, заменив каждый номер i2 на i3, то выполнив операцию композиции с каждой тройкой номеров вершин i1, i2, i3, получим из графа G1 граф G3. Итак, получается, что отношение изоморфизма между графами есть отношение эквивалентности, а множество изоморфных графов образует класс эквивалентности. Это означает, что все свойства графа мы можем рассматривать «с точностью до изоморфизма», то есть для всего класса изоморфных (эквивалентных) графов. Именно отсюда проистекает понятие инвариантов – числовых характеристик, одинаковых для всех изоморфных графов. Основные инварианты графа – это число вершин p и число ребер q. В регулярных графах инвариантом является степень регулярности n. Для нерегулярных графов мы можем рассматривать, например, такие инварианты, как максимальная степень вершины rmax, минимальная степень вершины rmin, число вершин заданной степени k и т.п. По мере изучения мы введем в рассмотрение еще ряд полезных инвариантов. Но, к сожалению, не существует набора инвариантов, который бы однозначно описывал весь класс эквивалентных графов. Именно поэтому для поиска изоморфных графов в общем случае приходится использовать перебор.
Подграфы и части. Операции над графами. Подграфы. Основные определения. Граф G ’ называется подграфом графа G, если V ’Ì V и E ’Ì E. Если в графе G ’ нет изолированных вершин, можно ограничиться только условием E ’Ì E.
Граф G ’ называется остовным подграфом графа G, если V ’= V. Ясно, Нуль-граф { V ’= V, E ’=0} тоже является остовным подграфом G. Граф G ’ называется индуцированным подграфом на графе G, если " v iÎ V ’, v jÎ V ’ (v i, v j)Î E Þ(v i, v j)Î E ’. Ясно, что если остовный подграф одновременно является индуцированным, то он совпадает с самим графом G.
Операции над графами. Поскольку граф - это однородное бинарное отношение на V2, то, казалось бы, операции над графами будут те же самые, что и для отношений. Давайте посмотрим, что происходит на самом деле. Во-первых, чтобы выполнять некоторые операции, нам нужно ввести понятие «универсума». Если мы примем за универсум полный неориентированный граф на p вершинах, то относительно операций над ребрами, то есть на множестве E, мы можем построить булеву алгебру (вспомним представление графов матрицей смежности). Минимальным элементом у нас тогда будет нуль-граф, максимальным – полный неориентированный граф, и можете сами проверить, что все законы логики (то есть соответствующие им свойства операций над множествами ребер) будут выполняться. Но поскольку граф, по определению, - конструкция из двух множеств, операции над графами рассматриваются не только как операции на множестве ребер, но и как операции на множестве вершин. Начнем с операций добавления и удаления элементов графа. Удаление ребра e приводит к образованию графа G ’, где V ’= V & E ’= E \{ e }. Ясно, что добавление ребра образует граф G ’, где V ’= V & E ’= E È{ e }. То есть множество–носитель отношения не меняется. А что же происходит при операциях с вершинами? Удаление вершины v приводит к образованию графа G ’, где V ’= V \{ v } & E ’= E \{ e i | e i=(v i, v) Ú e i=(v, v i)}. Но здесь заметим, что для полных графов K 3\{ v }= K 2, K 4\{ v }= K 3,…, K n\{ v }= K n-1, n =| V | (попробуйте сами объяснить, почему). Посмотрим теперь, как добавлять элементы графа. Здесь тоже есть нюанс. Просто добавление вершины v – это расширение множества V: V ’= V È{ v }. Но есть еще операция стягивания графа G к вершине v. В результате этой операции образуется граф G ’, где V ’= V È{ v } & E ’= E È{ e =(v, v i), i=1,…,| V |}. Таким образом, для полного графа операция стягивания является обратной к операции удаления вершины. Но только для полного графа. Теперь перейдем от операций с элементами графа к операциям над графами в целом. Просто под дополнением Объединением графов G 1È G 2 при V 1Ç V 2=Æ называется граф G ’, где V ’= V 1È V 2 & E ’= E 1È E 2. В случае V 1Ç V 2=Æ операцию объединения графов называют прямой суммой.
В принципе, операцию объединения нетрудно распространить и на случай V 1Ç V 2¹Æ, обозначив V 3= V 1Ç V 2. Тогда мы получаем, что V ’= V 3È(V 1- V 3)È(V 2- V 3), где (V 1- V 3)Ç(V 2- V 3)=Æ. На V 3 мы выполняем объединение как операцию над бинарными отношениями, а на (V 1- V 3)Ç(V 2- V 3) - по правилу объединения графов. Заметим, что в данном случае мы рассматривали графы с фиксированной нумерацией вершин, то есть без учета изоморфизма. Но свойства графов, в том числе и свойства операций, мы обязаны рассматривать для всего класса изоморфных графов и тогда должны предполагать, что V 1Ç V 2=Æ. Соединением графов G 1+ G 2 при V 1Ç V 2=Æ называется граф G ’, где V ’= V 1È V 2 & E ’= E 1È E 2.{ e ij=(v i, v j), i=1,…, p 1, j=1,…, p 2}.
Заметим, что в результате соединения полных графов мы опять получаем полный граф. А вот в результате соединения двух нуль-графов мы получаем очень интересную конструкцию, которая называется двудольным графом. Причем не просто двудольным, а так называемым полным двудольным графом. Такие графы обозначают Km,n, где m = p 1, n = p 2.
14. Маршруты, цепи, циклы. Понятие связности и достижимости. Взаимосвязь числа компонент связности с основными инвариантами графа. Графы и бинарные отношения. Транзитивное замыкание. Маршрутом в графе называется любая последовательность попарно смежных (в орграфе – непосредственно достижимых) вершин { v 0, v 1,…, v k}. В маршруте как вершины, так и ребра могут повторяться. Если v 0 = v k, то маршрут называется замкнутым, в противном случае – открытым. Если в маршруте каждое ребро встречается ровно один раз, то такой маршрут называется цепью. Если при этом в цепи каждая вершина встречается только один раз, то такая цепь называется простой цепью. Замкнутая цепь называется циклом (в орграфе – контуром), соответственно, замкнутая простая цепь называется простым циклом. Чтобы решать любые задачи обхода графа, необходимо ввести понятие связности. Связным называется граф, любые две вершины которого соединены простой цепью. При большом количестве ребер таких цепей можно построить много. Какие-то из них будут короче, какие-то длиннее. Самая короткая из цепей, соединяющих две вершины графа, называется геодезической, а ее длина – расстоянием между вершинами. Самая длинная геодезическая называется диаметром графа. Для ориентированных графов понятие цепи, следовательно, и понятие связности можно ввести только при снятии ориентации ребер. Если же учитывать ориентацию, то мы обязаны будем ввести какие-то дополнительные понятия. В этом случае нам придется рассматривать не цепи, а пути.
Путем в орграфе называется последовательность вершин, непосредственно достижимых одна из другой. Замкнутый путь называется контуром. Покажем, что связность есть отношение эквивалентности. Связность рассматривается как достижимость одной вершины из другой при отсутствии ориентации ребер, то есть (u, v)=(v, u) " u, v Î V. Топологическим минором графа G называется граф G ’, который получается в результате склеивания некоторых смежных вершин из G. Операция склеивания вершин vi и vj называется еще стягиванием ребра e =(vi, vj). При стягивании ребра (vi, vj) все отношения смежности, которые были у вершин vi и vj, переходят к новой вершине v (рис.3.6). Но при этом если для какой-то вершины v k существовала пара ребер (vi, vk) и (vj, vk), то эта пара превращается в одно ребро (v, vk).
Ясно, что если мы стягиваем неориентированное ребро, то мы не теряем никакой информации о связности вершин графа, поскольку можем пройти по ребру в любом направлении. А вот если мы стянем ориентированное ребро, то здесь мы можем либо потерять некоторые пути, либо получить лишние. Поэтому говорить про достижимость вершины самой из себя на орграфе некорректно. Под рефлексивностью тогда следует понимать возможность опять вернуться в эту вершину после выхода из нее. Т.е. в графе должен существовать замкнутый контур, включающий эту вершину. Кстати, в этом случае мы, возможно, кое-что сможем и склеить без потери информации. Свойства отношения «связность». Рефлексивность. Если граф неориентированный, то, выйдя из какой-то вершины, мы всегда можем вернуться в нее назад, поскольку можем двигаться по ребру в любом направлении. Симметричность. Если из vi можно попасть в vj, то по любой из цепей, соединяющих vi и vj, можно попасть обратно. Транзитивность. Если из vi можно пройти в vj, а из vj в vk, то через vj можно пройти из vi в vk. Если граф связен, то мы можем обойти его за один проход, но только если он неориентированный. Для ориентированных графов дело обстоит сложнее. Именно для них и возникает понятие достижимости, поскольку мы будем двигаться только по исходящим дугам и в какой-то момент можем оказаться в вершине, у которой таковых нет. Орграф Gd называется связным, если связен граф, который получается из Gd при снятии с ребер ориентации. То есть если между каждой парой вершин существует либо путь S (v i, v j), либо путь S (v j, v i). Посмотрим теперь, какому типу отношения соответствует понятие достижимости. Легко проверить, что будет выполняться транзитивность. Если граф строго ориентированный, а не смешанный, то отношение будет антисимметрично. Т.е. отношение частичного порядка мы уже получили. Теперь - рефлексивность. Рефлексивностью - возможность возвращения в вершину по какому-то маршруту. В случае ориентированного графа это получается замкнутый путь - контур. То есть если в ориентированном графе существуют контуры, это уже отношение нестрогого частичного порядка, а отношению строгого частичного порядка будет соответствовать бесконтурный ориентированный граф.
Матрица достижимости и транзитивное замыкание. Матрицей достижимости называется матрица M размерности p ´ p, где mij =1, если vi достижима из vj, и mij =0 в противном случае. Для связного неориентированного графа такая матрица будет состоять из одних единиц. Причем по диагонали тоже будут стоять единицы, потому что, походив-походив по графу, мы всегда можем вернуться назад, хотя бы тем же самым путем (не так, как в задаче о 7 мостах). А вот для ориентированного графа матрица M будет другой. И по ее виду мы можем понять, какой тип отношения порядка задает граф Gd. Если по диагонали будут одни нули, значит, это отношение строгого частичного порядка, поскольку имеет место антирефлексивность. В противном случае мы имеем отношение нестрогого частичного порядка. Определяя транзитивность, мы писали такое выражение R o R Ì R. То есть отношение транзитивно, если оно замкнуто относительно операции композиции. R образует полугруппу относительно операции композиции. Если отношение задано бинарной матрицей A размерности n ´ n, то операция композиции есть логическое произведение A × A. A × A для матриц непосредственной достижимости- это матрица путей, состоящих из двух ребер, то есть матрица достижимости одной вершины из другой за два шага. Тогда A × A × A есть матрица достижимости одной вершины из другой за три шага, и так далее. Ясно, что таких шагов t будет не более чем p -1, причем t = p -1, только если диаметр графа есть p -1. Значит, в общем случае, чтобы получить полную матрицу достижимости, мы должны объединить все пути длиной от 1 до p -1 ребра. Итак, имеем: Вспомним что такое замыкание отношения относительно некоторого свойства (Пусть R и R’ – однородные отношения на множестве A. Отношение R’ называется замыканием отношения R относительно свойства C, если 1) R’ обладает свойством C; 2) R является подмножеством R’: RÌR’; 3) R является наименьшим среди всех R’’, таких что имеет место C(R’’) и RÌ R’’.) и обратим внимание, что здесь мы как раз и имеем случай такого замыкания. Матрица M объединяет все варианты путей - отношений достижимости между парами вершин, то есть является надмножеством над всеми возможными путями - отношениями. При этом она не включает ничего лишнего, только простые цепи. То есть это минимальное надмножество, обладающее свойством транзитивности. Поэтому матрицу M называют иначе транзитивным замыканием отношения достижимости. Подмножества вершин графа, образующие классы эквивалентности относительно отношения связности, называются компонентами связности или связными компонентами (рис.3.7).
К аждый граф единственным способом представим в виде прямой суммы своих связных компонент. Для графа, состоящего из нескольких связных компонент, матрица достижимости будет состоять не только из одних единиц. Используя понятие изоморфизма, мы можем перестановкой строк и столбцов привести ее к блочно-диагональному виду и определить, сколько в нашей конструкции связных компонент, а также размеры этих компонент. Каждой компоненте будет соответствовать определенный блок из единиц вдоль диагонали. Число компонент связности k является инвариантом графа, так же, как число вершин p и число ребер q. Если k =1, то мы имеем просто связный граф. Для решения некоторых задач, например, для построения топологической модели очень большой сети, важно заранее знать, будет ли данный граф связным. Или же сделать приблизительную оценку числа компонент связности, без построения матрицы достижимости и приведения ее к блочно-диагональному виду. Для этого можно использовать следующее отношение между основными инвариантами графа. Теорема. Пусть p – число вершин, q – число ребер, k - число компонент связности графа. Тогда
Докажем левую часть отношения. Для того чтобы соединить p точек, нужно, по меньшей мере, p -1 ребро, то есть q ³ p-1. Если в графе k компонент связности, каждая из которых содержит p i вершин (i=1,…, k), то, просуммировав неравенства для ребер по всем k компонентам, получаем искомую нижнюю оценку. Правую часть отношения докажем, используя, наоборот, полные графы, в которых число ребер максимально. Самое большое число ребер в графе, состоящем из k компонент связности, будет в том случае, когда он представляет собой прямую сумму полных графов. Полный граф, в свою очередь, имеет Теперь осталось выяснить, при каком числе k общее число ребер будет максимально. В результате операции соединения двух полных графов у нас опять получается полный граф. Такое соединение добавляет D q = p 1× p 2/2 ребер. Общее число ребер в двух соединяемых связных графах равно q =1/2[(p 1+ p 2)(p 1+ p 2-1)- p 1× p 2], следовательно, q будет тем больше, чем меньше величина D q = p 1× p 2/2 - число добавляемых ребер. Минимальное же количество ребер добавляется при добавлении одной вершины: p 2=1, D q=p 1 - 1. То есть максимальное количество ребер в графе из k компонент будет тогда, когда одна компонента – полный граф, а остальные – изолированные вершины. Число ребер в таком графе q =(p - k)(p - k +1)/2. Отсюда имеем искомое неравенство. Следствие. Если q >(p -1)(p -2)/2, то граф связен.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.176 (0.016 с.) |

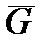 графа G подразумевается дополнение его до полного графа Kp, где p =|V|. Употребляется также дополнение графа G ’ до графа G. Его обозначают G - G ’. Точно так же, как мы определяли дополнение бинарного отношения. А вот с другими операциями дело обстоит иначе.
графа G подразумевается дополнение его до полного графа Kp, где p =|V|. Употребляется также дополнение графа G ’ до графа G. Его обозначают G - G ’. Точно так же, как мы определяли дополнение бинарного отношения. А вот с другими операциями дело обстоит иначе.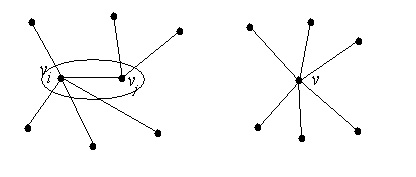
 .
.
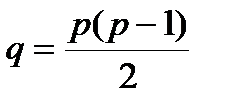 ребер.
ребер.


