
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические законы (тавтологии).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Минимальная дизъюнктивная нормальная форма. Если задача такова, что мы должны оперировать с полным набором двоичных переменных (или с фиксированным числом двоичных разрядов), то мы должны пользоваться СДНФ. Если же нам хочется использовать минимум двоичных переменных и основных операций (например, наиболее просто запрограммировать какое-то сложное логическое условие), лучше воспользоваться самым коротким представлением этой функции в дизъюнктивной или конъюнктивной нормальной форме. Такое представление называют, соответственно, минимальной дизъюнктивной нормальной формой (МДНФ) или минимальной конъюнктивной нормальной формой (МКНФ). Для сокращения ДНФ мы будем использовать набор простейших тавтологий, которые называют логическими законами. 1. Закон отрицания отрицания: 2. Закон идемпотентности: 3. Коммутативность: 4. Ассоциативность: 5. Дистрибутивность: 6. Закон нуля и единицы: 7. Законы де Моргана: 8. Законы поглощения: 9. Законы склеивания: Проверить любой из этих законов можно с помощью таблиц истинности или диаграммы Венна. Теперь же мы займемся получением МДНФ и доказательством более сложных тавтологий с применением логических законов. Для начала посмотрим, как через дизъюнкцию, конъюнкцию и отрицание выразить остальные операции. Штрих Шеффера и стрелка Пирса представляются через МДНФ согласно принципу двойственности (закон де Моргана): Импликация принимает значение 0 только на наборе (1,0). СДНФ для нее тогда будет такая: Эквивалентность имеет СДНФ Пример. Докажем следующую тавтологию: В соответствии с порядком выполнения логических операций последней будет выполняться импликация между скобками. Обозначим левую часть импликации буквой A, правую – буквой B и перейдем к ее дизъюнктивной нормальной форме: Подставив ДНФ для операции эквивалентности в этом выражении, перейдем к следующему: Используем для преобразования конъюнкции двух отрицаний закон де Моргана и далее применим дистрибутивный закон и закон нуля и единицы: Теперь займемся преобразованием правой части исходной импликации: В соответствии с законом поглощения (b Ú c)× b = b; отсюда получаем: Подставим результаты преобразований A и B в исходное выражение и продолжим преобразования, выполняя перегруппировку и используя закон нуля и единицы: Тавтология доказана. 4.Множества и подмножества.Универсально множество.Основные определения и свойства.Мощность множества,степень множества. Множество - некоторая совокупность абстрактных или реальных объектов, рассматриваемая как единое целое в рамках решаемой задачи. Математическая теория множеств оперирует с абстрактными понятиями, а не с конкретными объектами. Потому-то в абстрактной математической теории иногда возникают казусы, называемые парадоксами Способы задания множеств. Если множество состоит из небольшого числа элементов, то его можно задать простым перечислением. Если нет, то можно найти и сформулировать какое-то свойство, которым все эти элементы обладают, или условие, которому они удовлетворяют. Отсюда три способа задания множества: перечислением, предикатом (условием), или способом отбора элементов (алгоритмом порождения множества). Перечисление: A={ a 1, a 2,…, a n}. Пример: множество простых чисел из первого десятка натуральных чисел - A={1,2,3,5,7}. Предикатный способ: A={ a |P(a)}, где P(a) – условие (предикат), которому удовлетворяет а. Пример: множество положительных действительных чисел – A={a|a>0}. Порождающая процедура: A={ a | a =F}. Пример: множество из n нечетных положительных чисел - A={ a | a =2k+1, k=0,1,2,3,…n}. Если множество содержит очень большое количество элементов, его можно описать только предикатом или порождающей процедурой. Количество элементов, из которых состоит множество A, называется мощностью множества и обозначается M(A)=|A|. Объект a является элементом множества A, обозначают так: a ÎA. Если объект не является элементом A, пишут a ÏA. a ÎA – это элементарное высказывание, которое может быть либо истинным, либо ложным, но не то и другое вместе. Это высказывание часто называют предикатом принадлежности. В теории множеств совокупность объектов, из которой формируются множества конкретной модели, называют универсальным множеством или универсумом. Универсум принято обозначать буквой U. Множество состоит из отдельных элементов, значит, оно делимо и можно ввести еще одно понятие – подмножество множества А. Будем обозначать его Q(A) и писать, что Q(A)ÌA. Если Q(A) может совпадать с A, пишут Q(A)ÍA. Множество множеств иногда называют классом или семейством. Сколько же подмножеств мы можем сформировать из нашего конкретного множества А? Давайте заведем коробку, куда будем складывать элементы a i, назовем ее Q(A) и займемся комбинаторикой. Вначале наша коробка пуста, то есть " a i, i=1,…,|A| высказывание «a iÎA» ложно. Множество, не содержащее ни одного элемента, называют пустым и обозначают символом Æ. Итак, Q0(A)=Æ. Для него мы имеем набор истинностных значений высказываний «a iÎA» (набор логических переменных) - (0,…,0). Теперь кинем в коробку один элемент. Получим набор значений логических переменных (0,…,1). Уберем выбранный элемент и кинем другой. Получим набор (0,…,1,0). Потом будем кидать парами, тройками и так далее. Таких наборов для М двоичных переменных, как мы уже знаем (вспомните таблицы истинности) - 2|A|. Значит, мощность множества всех подмножеств заданного множества A мощности M(A)=|A| есть 2|A|, что соответствует количеству различных наборов из M булевых переменных. Множество всех подмножеств {Qi(A)} данного множества A поэтому называют булеаном. B(A)={Qi(A)|i=0,1,…, 2|A| }. Любому подмножеству конечного множества мощности n можно сопоставить элементарную конъюнкцию из n переменных, где каждой переменной x i соответствует высказывание «a iÎA». Сколько существует подмножеств заданной мощности N<M для нашего множества A? Способ расположения элементов в такой конструкции нас не интересует. Эта ситуация соответствует такому понятию комбинаторики, как число сочетаний из M элементов по N. Число возможных перестановок из N элементов PN=N!, число размещений из M элементов по N, с учетом их положения (с нумерацией элементов) Если не учитывать нумерацию элементов внутри подмножества (что и называется сочетанием), то это число будет в PN раз меньше: Степенью множества A называется его прямое произведение само на себя: An = A ´…´ A – всего n раз
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 834; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.19 (0.01 с.) |

 .
. .
. .
. .
. .
. .
. .
. .
. .
. =
=  ,
,  =
=  .
. . Попробуем получить более короткое представление. Самый короткий способ – воспользоваться СДНФ для ее антиоперации – разности. Она имеет очень простой вид:
. Попробуем получить более короткое представление. Самый короткий способ – воспользоваться СДНФ для ее антиоперации – разности. Она имеет очень простой вид:  Значит, импликацию можно записать так:
Значит, импликацию можно записать так:  . Воспользовавшись законом де Моргана, получаем:
. Воспользовавшись законом де Моргана, получаем:  .
. . Вряд ли нам удастся получить более короткое выражение. МДНФ для ее «антиоперации» – сложения по модулю 2 - получается через законы де Моргана и закон нуля и единицы:
. Вряд ли нам удастся получить более короткое выражение. МДНФ для ее «антиоперации» – сложения по модулю 2 - получается через законы де Моргана и закон нуля и единицы:  .
.
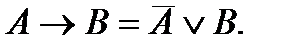 Такой прием позволит нам избавиться от антидизъюнкции:
Такой прием позволит нам избавиться от антидизъюнкции: 





 .
. . Итак, |{Qi}|=
. Итак, |{Qi}|=  .
.


