Решение задач из модуля Networks

Рассмотрим сначала решение трёх простейших задач из раздела сетевые модели. Они реализованы в программе QM в модуле Networks.

В этом модуле предполагается решение трёх частных задач, объединяет которые то, что все они могут быть представлены схематично в виде сети дорог, коммуникаций и т. п. Создавая файл исходных данных, вы получаете возможность выбрать ту или иную задачу из списка задач:

Соответствующий список задач следующий:

· минимизация дерева расстояний;

· определение кратчайшего пути;

· определение максимального потока.

Рассмотрим их последовательно.

6.1.1. Минимизация дерева расстояний предполагает определение кратчайшей общей длительности пути, соединяющего все пункты сети друг с другом. Примером такой задачи может служить задача по определению минимального расхода провода для соединения всех пунктов сети с центральным телефонным узлом или для создания компьютерной кабельной сети с центральным сервером.

Алгоритм решения такой задачи предполагает реализацию трёх пунктов:

1. Произвольно выбирается узел сети, который соединяется с узлом сети с кратчайшим расстоянием до него.

2. Выбранные узлы образуют множество соединённых узлов, а остальные – множество несоединённых узлов. Определяем узел несоединённого множества с кратчайшим расстоянием до соединённого множества. Соединяем эти два узла. В случае нескольких равных кратчайших расстояний выбираем для соединения любой из этих узлов.

3. Если все узлы сети соединены, то решение заканчиваем, в противном случае переходим к пункту 2.

Рассмотрим пример. Пусть дана сеть:

Рисунок 6.1 – Схема дорог для задачи минимизации дерева расстояний

 

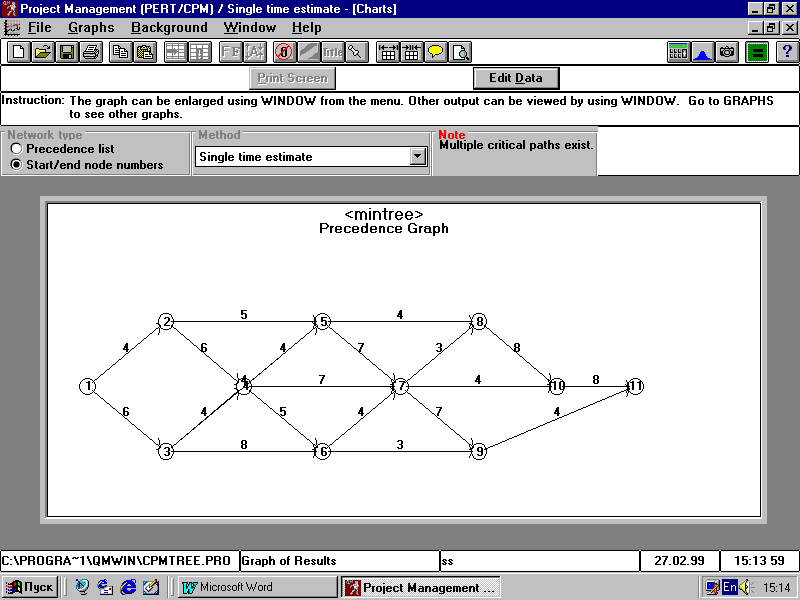
Поместим данные этой задачи в окно исходных данных программы. Нумерацию пунктов будем вести в соответствии с рисунком 6.1. Зададим число дуг сети, равное 19, и введём в таблицу исходные данные. Получим после решения:

Рисунок 6.2 – Окно исходных данных и решение задачи минимизации дерева расстояний

В этом окне помечены ветви, вошедшие в решение задачи. Если соединить узлы сети по этим ветвям, то получим минимальный расход провода, равный 39 единиц.

6.1.2. Задача определения кратчайшего пути в сети соответствует своему названию и определяет кратчайший путь от исходного узла сети до завершающего, если не указывать, откуда и куда необходимо двигаться. Алгоритм решения такой задачи состоит из пяти пунктов.

1. Начальный узел сети определяем как элемент постоянного множества и затем определяем смежные с ним узлы.

2. Определяем среди смежных узлов узел с кратчайшим расстоянием до какого либо узла постоянного множества.

3. Фиксируем эту ветвь и вычёркиваем другие ветви, соединяющие элементы постоянного множества с выбранным узлом смежного множества, но имеющие большую длину.

4. Присоединяем выбранный узел к элементам постоянного множества.

5. Определяем новое смежное множество узлов. Если такового нет, то решение заканчиваем, в противном случае переходим к пункту 2.

Проиллюстрируем работу алгоритма на этом же примере (рисунок 6.1). Введём число ветвей, равное 19, и остальные установки по умолчанию. После ввода информации и решения задачи получим следующие результаты (рисунок 6.3):

Рисунок 6.3 – Окно решения задачи определения кратчайшего пути в сети

Как видим, кратчайший путь от первого до 11-го узлов проходит через узлы 1 – 3 – 6 – 9 – 11 и равен по длине 21 единице.

Кроме того, при необходимости можно вывести на экран или на принтер окно с матрицей расстояний между всеми пунктами сети.

6.1.3. Задача определения максимального потока в сети позволяет определить максимальную пропускную способность сети, например, при перекачке нефти по системе трубопроводов, воды по системе ирригационных каналов, пропуске электроэнергии по системе линий передач и т. д. При формулировке задач такого типа необходимо указывать пропускную способность каждой ветви в обоих направлениях.

Алгоритм решения такой задачи состоит из трёх пунктов.

1. Определяем произвольный путь от начального узла сети к конечному с положительной пропускной способностью для каждой ветви этого пути. Если такового нет, процесс решения заканчивается.

2. Определяем в выбранном пути ветвь с минимальным потоком. Эту минимальную величину обозначим через с и припишем каждой ветви выбранного пути.

3. Уменьшим пропускную способность текущего потока для каждой ветви выбранного пути на величину с в прямом направлении и увеличим в противоположном. Последнее позволяет определить потенциальную возможность для каждой ветви сети. Затем переходим к пункту 1.

Проиллюстрируем работу этого алгоритма на ранее рассмотренном примере, подразумевая цифры у ветвей под пропускной способностью ветви в прямом и обратном направлении. После ввода информации и решения задачи получим:

Рисунок 6.4 – Окно решения задачи определения максимального потока

 

Здесь приведено лишь одно окно, показывающее результаты итераций. Из рисунка 6.4 видно, что решение закончено в две итерации и максимальный поток равен 8 ед. и проходит через ветви, указанные в полных путях каждой итерации. Кроме этого, можно вывести на экран окно, в котором указана исходная информация и результаты решения для каждой ветви сети.