
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод критического пути (СРМ)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выберем из этого списка первую процедуру и после заполнения диалогового окна, отметив, что будем анализировать 11 работ, и для каждой работы сети будем указывать номера начальных и конечных событий (Start/end node numbers). После заполнения таблицы исходных данных и решения задачи получим следующие окна отчётов о решении (рисунок 6.6).
Рисунок 6.6 – Окно результатов решения задачи методом СРМ
В этом окне указаны последовательно по столбцам: список работ, начальный узел работы (номер начального события), конечный узел, время выполнения работы, раннее начало, раннее окончание работы, позднее начало, позднее окончание и резерв времени работы. В первой строке таблицы указана длительность критического пути (Project), которая для рассматриваемого примера равна 31, и, кроме того, в последнем столбце на мониторе компьютера красным цветом выделены критические работы сети. Выбрав второе окно отчёта о решении задачи (Charts) – графики (диаграммы), получим графическое окно, в котором показан линейный график сети или линейная диаграмма проекта или график Гантта по ранним срокам начала работ (рисунок 6.7):
Рисунок 6.7 – График Гантта по ранним срокам начала работ
Здесь линейный график сети вычерчивается в масштабе времени, и по нему можно видеть, в какое время, какие работы выполняются, какие уже выполнены и какие ещё предстоит выполнить. По вертикальной оси графика отражены работы с их номерами в сети, а по горизонтальной – время. Кроме того, красным цветом на мониторе (серым – на рисунке 6.6) выделены критические работы. Такие графики удобны для анализа сети с использованием преимуществ графического отражения сети в масштабе реального времени. При необходимости можно вывести на экран аналогичные графики для поздних сроков окончания работ, смешанный график, объединяющий два первых и, наконец, четвёртая – исходный график сети, помещённый на рисунке 6.5. Программа предусматривает возможность представления сети в виде, отличном от описанного выше. Если при вводе исходной информации выбрать тип сети Precedence list – список предшествующих работ, то график сети будет иной: кружочки будут означать работы, а линии – связи между ними.
PERT-сети Рассмотрим далее следующую команду мены File – New – Triple time estimate (тройное время оценивания). Как уже отмечалось, здесь речь пойдёт о методе PERT, т.е. о стохастической сетевой модели, в которой оценка времени выполнения работ даётся тремя величинами. А именно: Optimistic time – оптимистическая оценка времени выполнения работы, т.е. время выполнения работы в наиболее благоприятных условиях (обозначим его через а), Most Likely – наиболее вероятная оценка времени выполнения работы (m) и Pessimistic time – пессимистическая оценка времени выполнения работы – время выполнения работы в наиболее неблагоприятных условиях (b). Средняя или ожидаемая оценка времени выполнения работ (Activity time), их дисперсия (Variance), а также стандартное отклонение (Standard Deviation) рассчитываются из предположения, что среднее время подчинено b-распределению и, в соответствии с этим, определяются из соотношений: tср = (a + 4m + b)/6, S2 = (b – a)/6, S = Далее расчёты ведутся в соответствии с методом СРМ. Определение оценки длины критического пути сопровождается вычислением стандартного отклонения этой оценки из соотношения: Sкр.пути = Для иллюстрации работы метода приведём ранее рассмотренный пример сети (см. рисунок 6.5) в предположении тройной оценки времени выполнения работ. После ввода исходной информации и решения задачи получим следующие окна, в которых отражены и исходная информация, и результаты решения (рисунок 6.8).
Рисунок 6.8 – Окно с исходными данными и с решением задачи PERT
Работы критического пути на мониторе выделены цветом, а в последних двух строчках окна помещены соответственно дисперсия и стандартное отклонение критического пути.
Рисунок 6.9 – Окно расчёта временных характеристик сети PERT
В окне на рисунке 6.9 указаны временные характеристики работ сети, рассчитанные на основе ожидаемого времени выполнения каждой работы, а также стандартное отклонение для каждой работы. Кроме того, в первой строке окна указаны среднее время окончания проекта (tср.пр. = 34,33 ед.) и его стандартное отклонение (Sпр. = 3,26). В этом методе имеется возможность вывести на экран четыре графических окна, как и в методе СРМ. Рассмотрим возможность использования вероятностных характеристик для определения вероятности окончания проекта в заданный срок. Известно, что в соответствии с центральной предельной теоремой статистики среднее время окончания проекта подчиняется нормальному закону распределения с вычисленными характеристиками (tср.пр. и Sпр.). Вероятность того, что проект будет закончен в срок (34,33), равный ожидаемому (среднему) времени завершения проекта, равна 0,5. Для вычисления вероятности окончания проекта в срок, отличный от ожидаемого, можно воспользоваться имеющейся в рассматриваемой программе процедурой вычисления характеристик нормального закона распределения. Вызвать её можно, щелкнув мышью по соответствующей кнопке на панели инструментов. После этого появится диалоговое окно (рисунок 6.10). Если выбрать процедуру вычисления величины по заданной вероятности, как это указано на этом рисунке (в блоке Compute – вычислить включена кнопка Value(s) given probability – величина по заданной вероятности), то определяются соответствующие границы доверительного интервала (рисунок 6.11).
Рисунок 6.10 – Диалоговое окно нормального распределения
Рисунок 6.11 – Окно с доверительным интервалом для метода PERT
Как видим, с вероятностью 0,95 проект будет закончен между 27,9 и 40,77 дней. Допустим, мы хотим определить вероятность того, что проект будет закончен между 30 и 38 днями. Для этого в диалоговом окне включим кнопку Probability given value(s) – вероятность по заданной величине и в появившихся окнах зададим эти величины. Получим (рисунок 6.12).
Рисунок 6.12 – Окно вычисления вероятности по заданной величине времени окончания проекта в методе PERT
Итак, вероятность завершить проект от 30 дней до 38 равна 0,775
СРМ с сокращением Третья процедура этой программы Crashing позволяет решать задачу частичной оптимизации сетевого графика по критерию “время – стоимость”– сокращение критического пути на максимально возможную величину при минимизации дополнительных расходов. При постановке этой задачи сначала предполагается, что работы сети могут выполняться в нормальных условиях при нормальной стоимости их выполнения, но могут выполняться и в ускоренном варианте, при этом стоимость выполнения работ возрастает пропорционально времени сокращения срока выполнения. Алгоритм решения такой задачи включает два пункта. 1. Определяется критическая работа с минимальной стоимостью сокращения за единицу времени, и её выполнение сокращается на возможный срок. При наличии нескольких критических путей для сокращения выбирается общая критическая работа этих путей с минимальной стоимостью сокращения за единицу времени. Если таковой нет, то для сокращения выбираются работы с минимальной единичной стоимостью в каждом критическом пути. После этого сравнивается время их возможного сокращения. Из них выбирается минимальное время, и каждая из таких работ сокращается на эту минимальную величину. При выборе величины, на которую сокращается очередная работа, отслеживается, чтобы начальный критический путь оставался критическим до конца процедуры сокращения. 2. Сеть с измененной информацией пересчитывается. Затем определяется время выполнения каждой работы, величина дополнительного увеличения стоимости выполнения работ, общая стоимость выполнения работ и величина критического пути. Если есть работы для сокращения, осуществляется переход к пункту 2, в противном случае процесс заканчивается Покажем решение задачи сокращения критического пути на примере ранее рассмотренной сети, введя в неё необходимую дополнительную информацию. Диалоговое окно для создания нового файла в этой задаче аналогично ранее рассмотренному окну для метода СРМ. После ввода информации и решения задачи получим следующее окно отчёта о решении задачи (рисунок 6.13).
Рисунок 6.13 – Окно с отчётом о решении задачи сокращения критического пути
Как видим, для решения задачи сокращения критического пути потребовалась дополнительная информация о сроке выполнения каждой работы в ускоренном режиме (Crash time) и о стоимости выполнения работ в нормальном и ускоренном режимах (Normal Cost и Crash Cost). Остальная информация рассчитана на основе описанного алгоритма решения задачи. В столбце Crash cost/pd отражена стоимость сокращения за один период, в столбце Crash by показано время сокращения соответствующих работ в результате реализации описанного алгоритма, а в столбце Crashing coat – стоимость этого сокращения. Кроме того, в первой строке отчёта (Project) указана величина критического пути в нормальных условиях работы, равная 33 дня, и в условиях максимально возможного сокращения – 19 дней. В итоговой строке TOTALS содержится информация о стоимости выполнения проекта в нормальных условиях – 830 денежных ед., общий срок сокращения – 19 дней и общая стоимость сокращения – 157 единиц. Кроме этой информации, имеется ещё окно отчёта, в котором указано расписание (последовательность) сокращения работ и накопленная стоимость этго сокращения (рисунок 6.14).
Как видим, сначала сокращалась работа K на 4 дня, что привело к удорожанию работ на 30 ед., затем работа G на 5 дней с удорожанием работ уже на 80 ед. Затем работа A, J и, наконец, работа D на один день. Суммарное удорожание работ составило 157 ед. Составление бюджета сети Четвёртая процедура программы Project Management предполагает решение задачи составления бюджета сети проекта, если есть информация о стоимости выполнения всех работ, включённых в проект. При этом предполагается, что финансовые ресурсы, необходимые для выполнения каждой работы, расходуются равномерно в течение всего срока выполнения работы, поэтому стоимость выполнения работы в течение одного дна, например, рассчитывается делением общей стоимости выполнения работы на её продолжительность. Составление бюджета проекта предполагает определение расходов на каждую дату в отдельности и суммарное или накопленное финансирование на дату в течение всего срока реализации проекта. Причём подобное расписание финансирования осуществляется в двух вариантах – по ранним и по поздним срокам начала работ с использованием соответствующих линейных диаграмм проекта. Проиллюстрируем принцип составления бюджета проекта на уже рассмотренном примере, изменив для удобства стоимость выполнения некоторых работ. Приведём необходимые окна отчётов о решении такой задачи (рисунок 6.15 и рисунок 6.16). Рассмотрим только ранние сроки начала работ (для поздних сроков принцип тот же самый).
Рисунок 6.15 – Окно результатов расчётов по сети
Рисунок 6.16 – Окно с бюджетом сети по ранним срокам начала работ
Рисунок 6.17 – График линейной диаграммы проекта по ранним срокам выполнения работ
Принцип составления таблицы на рисунке 6.16 следующий. Как следует из рисунка 6.17, 1-я работа начинается в начальный период реализации проекта и заканчивается в 6-м периоде. Стоимость её выполнения 60 ед. (см. рисунок 6.15), значит, стоимость одного дня этой работы равна 10 ед. (60/6=10). Итак, 1-я работа требует расходов в первые шесть дней по 10 ед., что и отражено в первой строке таблицы на рисунке 6.16. Аналогично 2-я и 3-я работы. Далее, в соответствии с информацией из рисунка 6.15 и рисунка 6.17, видим, что 4-я и 5-я работы начинаются в свои ранние сроки в 6-м периоде и заканчиваются, соответственно в 10-м и 8-м периодах. Их финансирование отражено на рисунке 6.16 в 4-й и 5-й строках и т. д. В последних двух строках этой таблицы отражены результаты финансирования на дату (это сумма средств, необходимых для выполнения всех работ в этот период) и накопленная сумма, т. е. сумма средств, необходимых для финансирования всех работ, выполненных до этого периода, включая и сам текущий период. Аналогичная таблица составляется и для поздних сроков начала работ. Поскольку в этом случае финансирование части работ отодвигается на более поздний период, появляется возможность регулирования финансированием проекта в определённых пределах. Эти пределы отражены в графическом окне, в котором помещены графики зависимости суммарного финансирования в зависимости от времени. Такой график приведён на рисунке 6.18.
Рисунок 6.18 – График бюджета проекта по ранним и поздним срокам начала работ Как видим, уже в начале реализации проекта появляется возможность регулирования финансовыми потоками при оплате работ в зависимости от сроков их начала, не влияя на окончательные сроки реализации проекта. Особенно эта возможность расширяется между 10-м и 18-м периодами. Конечно, в первую очередь необходимо обратить внимание на своевременное финансирование критических работ.
Задания для выполнения лабораторной работы № 6 1. Решить и проанализировать задачи определения кратчайшего расстояния, наименьшего дерева расстояний и максимального пути. 2. Решить и проанализировать задачи CPM, PERT, сеть с сокращениями и составления бюджета сети. Для всех вариантов и всех задач сеть будет одна и та же (рисунок 6.19).
Рисунок 6.19 – Сеть для выполнения лабораторной работы Для своего варианта характеристики дуг возьмите из таблицы, подставив вместо n номер своего варианта, и полученные числа округлите до целого в сторону увеличения.
Для первого задания эти цифры – расстояния между пунктами или пропускная способность пути, а для сетей CPM – время выполнения работ. Для сетей PERT это время считать, как наиболее вероятное. Оптимистическое и пессимистическое время рассчитайте самостоятельно, отняв и прибавив к нему три дня. Для задания Crashing стоимость выполнения работ и время их сокращения рассчитайте самостоятельно из соображений, что стоимость работы без сокращения равна 2t + 9, а при сокращении – 3t + 10, где t – время выполнения работы. Работы можно сокращать на четверть срока их выполнения в нормальных условиях (округлять с увеличением). Например, у Вас 9-й вариант и вы определяете стоимость работы 7–9. Время её выполнения 6+9=15 дней. Тогда стоимость выполнения этой работы равна 2*15+9=39 ед., а стоимость после сокращения – 3*15+10=55 ед. Сокращать эту работу можно на [15/4]+1=4 дня, т.е. с 15 до 11 дней. Для задания Cost Budgeting стоимость и время выполнения работ возьмите из предыдущей задачи до сокращения.
Лабораторная работа № 7 Управление запасами
При решении задачи управления запасами в основном необходимо ответить на два вопроса – когда запасы подлежат пополнению и чему равен объём пополнения запасов. А это, в свою очередь, необходимо для решения следующих двух задач – удовлетворить спрос на определённую продукцию и минимизировать суммарные издержки по обеспечению спроса на определённом уровне. Разработано большое количество моделей оптимального управления запасами. Из всего этого множества рассмотрим те из них, которые внесены в модуль Inventory программы QM (рисунок 7.1):
Рисунок 7.1 – Перечень задач в модуле Inventory · модель определения оптимального уровня запаса; · модель определения оптимальной партии изделий; · модель запасов с дефицитом; · модель определения оптимальной партии изделий с учётом возможного дефицита; · ABC анализ; · 7-я и 8-я модели определяют точку возобновления запаса и страховой запас в случае, когда спрос имеет нормальный и дискретный законы распределения. В зависимости от того или иного типа модели каждый раз оптимальный уровень запаса определяется из условия минимизации суммарных издержек, в которые включаются разные составляющие. При этом действуют разные предпосылки относительно времени реализации поставки. Рассмотрим последовательно реализацию первых пяти моделей из приведённого списка.
7.1 Модель определения оптимального уровня запаса Первая модель является базовой и определяется в предположении, что известны спрос на продукцию, издержки хранения единицы запаса и издержки оформления одного заказа, а также предполагается, что интенсивность расходования запаса постоянна, а поставка осуществляется мгновенно. Оптимальный уровень заказа в этом случае определяется из условия минимизации издержек хранения и заказывания. Обозначим их соответственно через THC и TOC. Тогда общие издержки составят: TIC = THC + TOC. Введём обозначения: Q – величина одного заказа; Cо – издержки оформления одного заказа; D – величина спроса на продукцию; Ch – издержки хранения ед. товара. Тогда, THC = Ch Q/2, a TOC = Co D/Q, следовательно, TIC = Ch Q/2 + Co D/Q. Минимизируя эту величину, получим известную формулу Уилсона: Q* = Приведём решение задачи по этой модели. Пусть D = 5 000, Co = 15, Ch = 5. Тогда Q* = Определим другие характеристики системы. THC = ch Q*/2 = 10 . 173,2/2 = 433, TOC = co D/Q* = 15 . 5000/173,2 = 433. Совпадение этих величин не случайно. В точке минимума суммарных издержек кривые издержек заказывания и хранения пересекаются, как это видно из рисунка 7.1. \ Рисунок 7.1 – Графическое решение задачи.
Прямая линия здесь характеризует издержки хранения (Holding Cost), равные (Q/2)Ch, гипербола – издержки заказывания (Setup Cost), равные (D/Q)Co. Верхняя линия – суммарные издержки (Total Cost). Как видим, точка минимума этих издержек совпадает с точкой, в которой издержки хранения и заказывания совпадают (нижние две линии пересекаются), решение задачи показано на рисунке 7.2.
Рисунок 7.2 – Решение задачи в модуле Inventory Поскольку в предположении этой модели поставка осуществляется мгновенно, а интенсивность расходования запаса постоянна, то максимальный уровень запаса совпадает с оптимальным и равен 173,21, а его средний уровень составляет половину оптимального и равен 86,6. При этом суммарные издержки запаса равны 866, а число заказов равно D/Q* = 29 (с округлением).
7.2. Модель определения оптимальной партии изделий При определении оптимальной партии изделий предполагается, что заказ поступает не мгновенно, а постепенно, с постоянной интенсивностью p, а запас расходуется с интенсивностью d, при чем, p > d, и, следовательно, пополнение запаса происходит с интенсивностью (p – d). За счёт того, что запас одновременно пополняется и расходуется, хранить приходится меньше и, следовательно, уменьшаются суммарные издержки. Оптимальный уровень заказа (оптимальная партия изделий) в этом случае определяется из соотношения: Q* = Максимальный уровень запаса в этой модели определяется из соотношения: Q*(1 – d/p), что, в отличие от предыдущей модели, меньше оптимального уровня заказа Q*. Пусть интенсивность пополнения заказа составляет p = 30 ед. в день, а интенсивность расходования заказа составляет d = 20 ед. в день. Определить оптимальный уровень заказа и другие характеристики системы в условиях предыдущей задачи. Имеем: Q* =
Рисунок 7.3 – Решение задачи в модуле Inventory
Модель запасов с дефицитом Эта модель реализует предпосылку, что иногда выгоднее иметь некоторое время неудовлетворённый спрос и за счёт этого уменьшить издержки хранения. Кроме того, в данной модели предполагается, что накопленный спрос удовлетворяется в первую очередь, и потому максимальный уровень запаса уменьшается по сравнению с оптимальным уровнем заказа на величину максимального уровня дефицита. Пусть эта модель имеет те же предпосылки, что и модель Уилсона. Обозначим через cs удельные издержки дефицита. Тогда оптимальный уровень заказа Q* и оптимальный уровень запаса I* определятся из соотношений Q* = Оптимальный уровень дефицита будет равен S* = Q*- I*. Период между поставками определится из T = Средний уровень запаса = Здесь суммарные издержки складываются из издержек заказывания, хранения и дефицита, а оптимальный уровень определяется из их минимизации. И потому издержки заказывания и хранения в оптимальной точке для этой модели не совпадают, как это было в предыдущих моделях. Продолжим решение предыдущего примера с учётом издержек дефицита. Для этого дополнительно необходимо указать издержки дефицита, которые примем равными 20. В модуле Inventory решение этой задачи показано на рисунке 7.4.
Рисунок 7.4 – Решение задачи в модуле Inventory
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 849; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.219 (0.01 с.) |



 .
.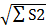 , где суммируются дисперсии ожидаемого времени выполнения критических работ.
, где суммируются дисперсии ожидаемого времени выполнения критических работ.





 Рисунок 6.14 – Последовательность сокращения срока выполнения работ
Рисунок 6.14 – Последовательность сокращения срока выполнения работ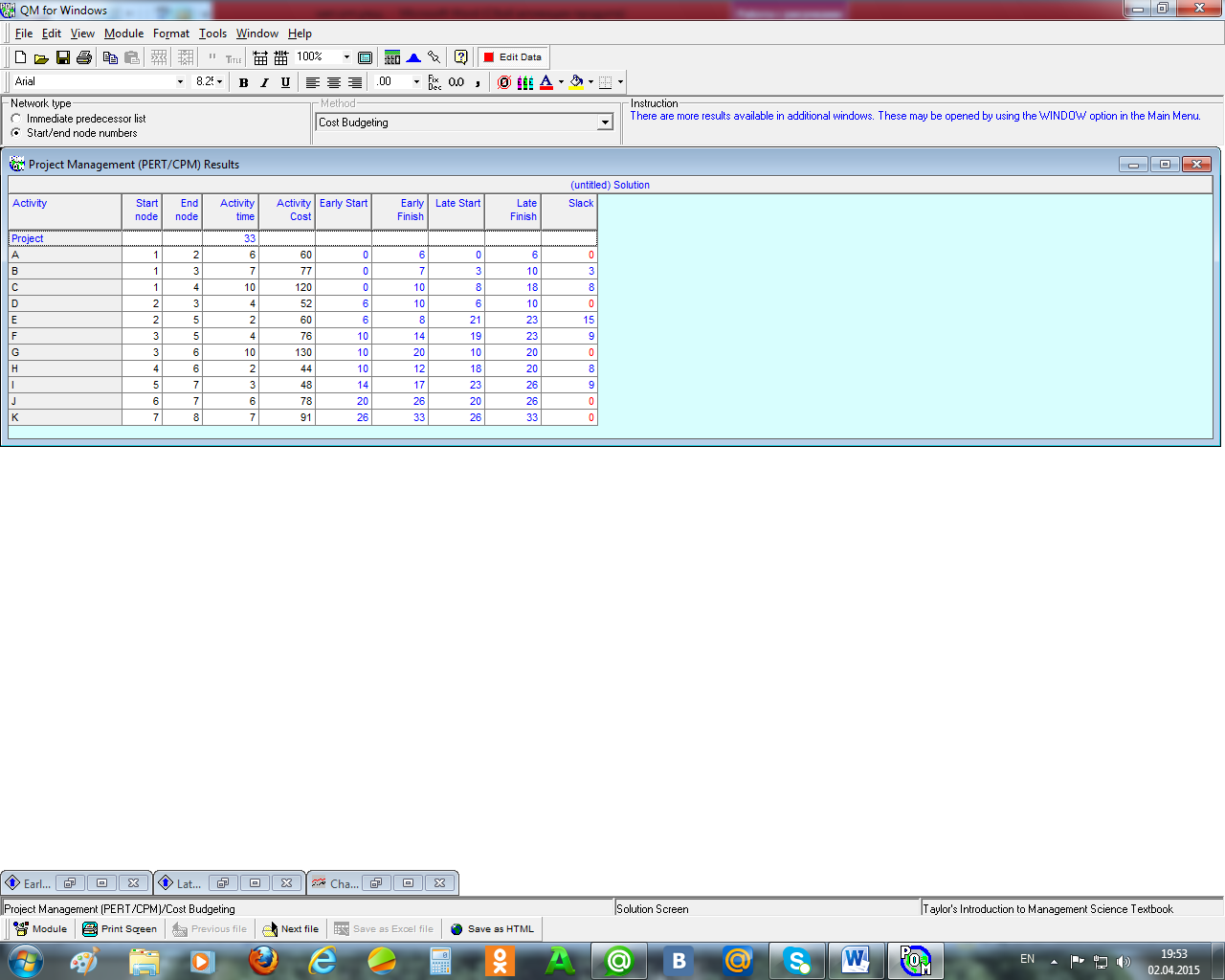




 .
.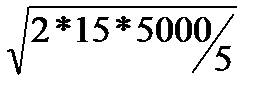 =173,2.
=173,2.

 .
. =300. Тогда максимальный уровень запаса составит: Q*(1 – d/p) = 300(1-1/3) = 100, а средний уровень – его половину, т.е. 50. Число периодов производства будет равно D/Q* = 5000/300 = 17 (с округлением). Издержки организации производства в этом случае составят 15
=300. Тогда максимальный уровень запаса составит: Q*(1 – d/p) = 300(1-1/3) = 100, а средний уровень – его половину, т.е. 50. Число периодов производства будет равно D/Q* = 5000/300 = 17 (с округлением). Издержки организации производства в этом случае составят 15  16,7 = 250, а издержки хранения – 50
16,7 = 250, а издержки хранения – 50 
 , I* =
, I* =  ,
, .
. , средний уровень дефицита =
, средний уровень дефицита = 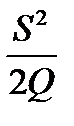 , число заказов =
, число заказов =  , тогда издержки хранения составят
, тогда издержки хранения составят 



