
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт равновесного выпуска и равновесных ценСодержание книги
Поиск на нашем сайте
Решим уравнение (1.6а) относительно Х, определив равновесный валовый выпуск отраслей, обеспечивающий заданный уровень спроса Y на конечную продукцию: X = (E – A)-1 Y. (1.7) Матрица В = (Е – А) –1 (1.8) называется обратной матрицей Леонтьева или матричным мультипликатором, (мультипликатором Леонтьева). Её элементы bij показывают потребность в валовом выпуске продукции i -й отрасли для производства единицы конечной продукции j -й отрасли и называются коэффициентами полных материальных затрат. Таким образом, В – это мультипликатор, показывающий эффект распространения спроса на валовую продукцию, первоначальным источником которого является спрос на конечную продукцию. Перепишем (1,7) с учётом (1,8) в виде X =B Y. (1.9) Эффект матричного мультипликатора рассчитывается из соотношения DX = B DY и отражает процесс распространения спроса на валовую продукцию DX, вызванный изменением спроса на конечную продукцию в объёме DY. Говорят, что решение системы уравнений МОБ позволяет определить равновесный выпуск, имея в виду под общим равновесием соотношение в экономической системе, которое характеризуется равновесием спроса и предложения всех её элементов. Определим равновесные цены, воспользовавшись системой уравнений производства продукции. Равновесные цены позволяют исследовать эффект распространения изменения цены, вызванный изменением элементов добавленной стоимости и построить ценовую модель МОБ. Обозначим через vj = zj / xj величину добавленной стоимости, приходящейся на единицу валовой продукции отрасли и называемой долей добавленной стоимости. Тогда, учитывая, что zj = vj xj, (1.2) перепишем в виде:
или Это выражение описывает формирование цен каждого вида продукции в базовом периоде, если их принять за единицу. Слагаемое Если для расчётного периода доля добавленной стоимости будет равна vj, то цены Pj (j =
В матричном виде эту систему можно переписать как Р = Ат Р + V. (1.13) Матрица Ат – транспортированная матрица А. Решим (1.13) относительно Р. Получим P = BT V. (1.14) Уравнения (1.12) и (1.13) называют моделью равновесных цен, а матрицу Вт – ценовым матричным мультипликатором. Эффект распространения DР, вызванный изменением доли добавленной стоимости на DV может быть рассчитан из (1.14): DP = BT DV.
Балансы трудовых ресурсов и основных производственных фондов Обозначим через L общую потребность в трудовых ресурсах, необходимых для выпуска продукции в объёмах L где tj – коэффициенты прямых затрат труда в j -й отрасли; tj = Lj / xj (Lj – объёмы затрат труда в j -й отрасли). Кроме того, дополним схему МОБ производства и распределения продукции балансом основных фондов
где fj – коэффициенты прямой фондоёмкости в j -й отрасли; fj = Фj / xj (Фj – наличие фондов в j -й отрасли). В матричной записи (1.15) и (1.16) примут вид L = t x, Ф = f x. Перепишем их с учётом (1.10), получим L = t x = t B Y = t Y; (1.17) Ф = f x = f B Y = j Y, (1.18) где t = t B или tk аналогично j = f B или j k Коэффициенты tk и jk называются соответственно коэффициентами полных затрат труда и фондов и показывают потребность в соответствующих ресурсах во всех отраслях национальной экономики для производства единицы конечного продукта в k -й отрасли. Соотношения (1.17) и (1.18) показывают, что прямые затраты ресурса на выпуск валовой продукции совпадают с их полными затратами на выпуск конечного продукта. Рассмотрим постановку задачи и последовательность её решения для выполнения лабораторной работы по обсуждаемой теме на конкретном примере.
Постановка задачи Цель – научиться использовать экономико-математическую модель межотраслевых связей в анализе межотраслевых пропорций на основе коэффициентов прямых затрат и эффектов мультипликаторов.
Задача. Дан следующий отчётный межотраслевой баланс (МОБ) (пример условный).
L 76 36 54 69 40 58
Ф 33 97 87 125 83 75
В шахматке указаны межотраслевые потоки промежуточной продукции, в последних двух строках за пределами таблицы – объёмы затрат труда и фондов, а в последнем столбце – конечная продукция. Будем считать, что номенклатура отраслей следующая: 1. Сельское, лесное и рыбное хозяйство. 2. Тяжёлая промышленность. 3. Лёгкая промышленность. 4. Строительство и энергетика. 5. Транспорт и связь 6. Услуги.
Задания для выполнения лабораторной работы №1 1. Построить таблицу отчётного МОБ, проверить основное балансовое соотношение. 2. Составить плановый МОБ при условии увеличения спроса на конечный продукт по отраслям на 5, 4, 6, 7, 3 и 8 %. 3. Рассчитать коэффициенты прямых и полных затрат труда и фондов и проверить в плановом балансе выполнение равенств (1.17) и (1.18), используя формулы (1.15) и (1.16). 4. Определить, на сколько процентов необходимо увеличить производительность труда по отраслям для выпуска планового валового продукта с той же численностью, что и в отчётном периоде. 5. Проследить эффект матричного мультипликатора при дополнительном увеличении конечного продукта по лёгкой промышленности на 5 %. 6. Рассчитать равновесные цены при увеличении зарплаты по всем отраслям на 10% (считать доли заработной платы в добавленной стоимости по отраслям следующими: 0,33, 0,5, 0,52, 0,35, 0,43, 0,6). Проследить эффект ценового мультипликатора при дополнительном увеличении зарплаты в сельском хозяйстве на 5%.
Ход выполнения работы Предполагается, что работа будет выполняться с помощью программы обработки электронных таблиц Microsoft Excel. 1. Заполним таблицу отчётного баланса.
Таблица 1.2 – Таблица отчётного МОБ
При составлении этой таблицы в Excel автоматически проверяется основное балансовое соотношение, суть которого состоит в равенстве суммарного конечного продукта (последняя ячейка столбца «Кон. продукт») и суммарной добавленной стоимости (последняя ячейка строки «Доб. ст-ть») в таблице 1.2 (2 482,54 = 2 482,54). При заполнении столбца и строки «итого» необходимо воспользоваться функцией суммирования, а в остальных случаях воспользоваться возможностью вычислений в ячейках с помощью формул и копировании формул в другие ячейки. Для составления таблицы планового баланса необходимо рассчитать плановый валовой выпуск по формуле (1.9) и плановые межотраслевые потоки по формуле (1.4), а дальше – как в отчётном балансе. Рассчитаем сначала коэффициенты прямых материальных затрат по формуле (1.5), используя информацию отчётного баланса. Поскольку элементы столбца межотраслевых потоков делятся на валовой выпуск потребляющей отрасли, записывая формулу (1.9) в соответствующей ячейке, воспользуемся абсолютной ссылкой для номера столбца. Тогда формула для вычисления, например, а11 будет иметь вид «=В4/В$12», если х11 находится в ячейке В4, а х1 – в ячейке В12. Относительная ссылка превращается в абсолютную нажатием клавиши ”F4” в режиме редактирования. В нашем случае эту клавишу надо нажать дважды, чтобы абсолютной осталась только вторая ссылка. Вычислив а11, скопируем эту формулу на весь столбец матрицы А, а затем этот столбец – на все столбцы матрицы. Получим следующую матрицу коэффициентов прямых материальных затрат:
Рассчитаем матрицу В по формуле (1.8), для чего сначала вычислим матрицу (Е–А), а затем найдём к ней обратную. На свободном месте листа Excel введём единичную матрицу Е размерности 6х6. Для расчёта матрицы (Е–А) введём формулу в свободную ячейку для вычисления элементов этой матрицы и скопируем её сначала по столбцу вниз, а потом – столбцы вправо. Рассчитаем теперь матрицу В = (Е – А) –1, используя функцию Excel вычисления обратных матриц. Для этого поместим курсор в начало массива, отведённого для матрицы В, щёлкнем на кнопке мастера функций fx, выберем категорию “математические”, а затем функцию «МОБР», щёлкнув по ней кнопкой мыши. Появится диалоговое окно работы с этой функцией. В поле «массив» необходимо указать адрес массива с матрицей (Е–А), для чего можно щелкнуть по «флажку» в конце этого поля, окно ввода при этом свернётся до строки поля, под строкой формул. В правой части этой строки будет виден тот же «флажок». После этого необходимо выделить курсором мыши массив с матрицей (Е–А) (при этом выделенный массив будет обведён мерцающим курсивом, а в начале строки появится адрес выделенного массива) и повторно щёлкнуть по этому же «флажку». При этом окно ввода приобретёт первоначальный вид. Щёлкнув по кнопке «ОК», завершим указание массива обращаемой матрицы. После этого необходимо выделить чёрным цветом место под массив, отведённый для обратной матрицы, затем щёлкнуть кнопкой мыши по строке формул (при этом адрес массива выделится синим цветом) и ввести формулу обращения матриц как формулу массива, нажав последовательно, не отпуская три клавиши “Ctrl” + “Shift” + “Enter”. Получим матрицу В:
Для расчёта планового валового выпуска по формуле (1.9) необходимо вычислить плановый конечный продукт, увеличив отчётный конечный продукт по каждой отрасли на 5, 4, 6, 7, 3 и 8 %. Получим
Рассчитывать и размещать его лучше сразу в таблицу для планового баланса при помощи копирования формулы во все его строки по столбцу «Кон. продукт». Для расчёта по формуле (1.9) воспользуемся функцией умножения матриц «МУМНОЖ» из мастера функций, выбрав категорию «математические». Эта функция имеет два поля ввода для указания перемножаемых массивов, как это указано на рисунке 1.1.
Щелчком по флажку поля «Массив 1» окно ввода сверните до строки массива, затем выделите массив с матрицей В, снова щёлкните по флажку и окно ввода развернётся до первоначального вида. После этого щёлкните по флажку «Массив 2» и аналогично предыдущему выделите массив столбца «Кон. продукт». Повторным щелчком по этому флажку окно ввода разверните до первоначального вида. А затем аналогично предыдущему: щёлкните по кнопке «ОК», выделите формулу, выделите место под массив вычисленного валового продукта и нажмите последовательность клавиш “Ctrl” + “Shift” + “Enter”. Получите
Этот результат можно разместить сразу в столбце «Вал. продукт» таблицы планового баланса. Для заполнения «шахматки» этой таблицы воспользуемся формулой (1.4). Для облегчения её использования разместим показатели валового продукта в последней строке таблицы и при записи формулы воспользуемся правилом организации фиксированной ссылки по второму адресу. Например, при вычислении х11 формула примет вид: «=C15*B$53», если а11 находится в клетке С15, а Х1 в клетке Б53. Как и в случае вычисления элементов матрицы А, фиксированная ссылка по второму адресу получается двойным нажатием клавиши «F4» после щелчка по клетке с адресом «Б53». После вычисления по этой формуле необходимо скопировать её сначала по столбцу таблицы, а затем столбец – по строкам. После соответствующих вычислений получим таблицу 1.3. Таблица 1.3 – Таблица планового МОБ
Тем самым будет выполнен п.2 задания лабораторной работы.
3. Для выполнения п.3 работы рассчитаем коэффициенты прямой трудоёмкости и фондоёмкости. Расчёты проводим по формулам: tj = Lj/Xj, fj = Фj/Xj, копируя их в соответствующие клетки. Получим
Рассчитаем коэффициенты полных затрат труда и фондов по формулам (1.19) и (1.20) соответственно, используя функцию умножения матриц, как при вычислении планового валового выпуска. При этом необходимо учитывать, что матрицы t и f – это строки и поэтому результаты вычисления так же будут строками.
Подсчитаем плановую потребность в труде и фондах, используя формулы (1.15) и (1.16), для чего эту потребность сначала рассчитаем отдельно по отраслям, а затем просуммируем. Получим
Первые 6 цифр – это потребность по отраслям, последняя – по всей экономике. Воспользуемся теперь второй частью формул (1.17) и (1.18), для чего умножим матрицы коэффициентов полных затрат ресурсов на конечный продукт в плановом балансе. Получим
Что доказывает равенство прямых затрат ресурсов на производство валового выпуска и полных затрат ресурсов на производство конечного продукта.
4. Для выполнения четвёртого пункта рассчитаем производительность труда по валовому продукту в отчётном периоде и в плановом, но численность возьмём в обоих случаях из отчётного баланса, а затем сравним эти результаты. В отчётном периоде производительность труда по валовому продукту определяется делением величин валового продукта по отраслям на соответствующую численность. Получим
Разделив валовой продукт планового периода на ту же численность, получим
Как видим, производительность труда должна увеличиться. Определим, на сколько процентов. Разделив одно на другое, получим
Наибольшее увеличение производительности труда при этом потребуется для 6-й отрасли – «услуги», на 7,45 %. 5. Эффект матричного мультипликатора определим, пользуясь соотношением DX = B DY. DY рассчитаем из условия дополнительного увеличения спроса на конечный продукт по 3-й отрасли (лёгкой промышленности) на 5 %. Итак, спрос на конечную продукции по всем отраслям, кроме 3-й, останется прежним, т. е. прирост спроса по этим отраслям будет равен нулю, а по 3-й отрасли такой прирост будет равен (324,72*0,05 = 16,236). Окончательно получим, DY = (0 0 16,236 0 0 0)Т, Перемножив B и DY, получим DX = (0,48 2,29 26,65 2,52 1,39 4,57)Т. Как видим, изменение спроса на валовую продукцию произошло по всем отраслям. В процентном соотношении это составит (0,28 0,28 1,8 0,27 0,31 0,23). 6. Равновесные цены определим из соотношения P = BT V, а доли добавленной стоимости рассчитаем по формуле vj = zj / xj, изменив их затем из условия 10%-го увеличения зарплаты. Разделив добавленную стоимость по отраслям на валовый выпуск, получим
Выделим зарплату, воспользовавшись информацией из задания в п. 6 о долях зарплаты в добавленной стоимости. Получим
Добавив 10 % от полученных величин к ранее рассчитанным показателям, получим требуемую величину доли добавленной стоимости для расчёта равновесных цен. Итак, V равно
Для расчёта равновесных цен по приведённой формуле необходимо протранспонировать матрицу коэффициентов полных затрат В. Воспользуемся функцией транспонирования из мастера функций, выбрав из категории «Ссылки и массивы» функцию «ТРАНСП». В появившемся окне ввода укажите массив матрицы В, предварительно установив курсор в начало массива, где будет размещена транспонированная матрица. Не забудьте, что это формула массива. Щёлкнув по кнопке «ОК», выделите массив размерности 6х6 чёрным цветом, активизируйте функцию транспонирования, щёлкнув по строке формул, и нажмите последовательно не отпуская клавиши “Ctrl” + “Shift” + “Enter”. В результате этого получите матрицу ВТ, умножив её на V, получим равновесные цены:
Не забудьте, что в соответствии с правилами умножения матриц вектор V перед умножением должен быть представлен в виде столбца. Как видим, результаты расчетов показали, что при 10%-ном росте зарплаты одновременно по всем отраслям цены на продукцию отраслей увеличились в пределах от 3,94 % до 5,74 %. Рассчитаем теперь эффект ценового мультипликатора при дополнительном увеличении зарплаты по отрасли «сельское хозяйство» на 5 %. Расчёты будем вести по формуле DP = BT DV, где DV определим из условия задачи. DV = (0,0095 0 0 0 0 0)Т. Тогда DP = (0,01105 0,0025 0,00034 0,0005 0,00031 0,00029). Как и ожидалось, наибольший прирост в цене продукции пришёлся на саму отрасль «сельское хозяйство» – на 1,1 %, а по остальным отраслям этот прирост составил доли процента. Например, по отрасли «тяжёлая промышленность» на 0,25 %. Эффект же ценового мультипликатора проявился в том, что при изменении цены только в одной отрасли произошло изменение цен во всех отраслях и это изменение можно отследить с помощью ценового мультипликатора BT.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 934; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.71.149 (0.012 с.) |

 (1.10)
(1.10) (1.11)
(1.11) показывает возмещение стоимости, а vj – вновь созданную стоимость (с учётом амортизации и налогов). Система равенств (1.11) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.
показывает возмещение стоимости, а vj – вновь созданную стоимость (с учётом амортизации и налогов). Система равенств (1.11) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.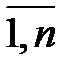 ) будут определяться по (1.11) из соотношений
) будут определяться по (1.11) из соотношений . (1.12)
. (1.12)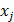 , (j = 1,2,…,n). Тогда
, (j = 1,2,…,n). Тогда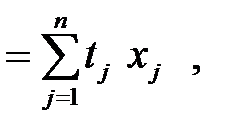 (1.15)
(1.15) (1.16)
(1.16)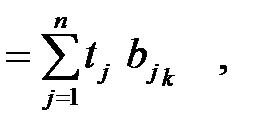 (1.19)
(1.19) (1.20)
(1.20)



