Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор оптимальной стратегии в условиях неопределённости (игры с природой)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выше рассмотренная задача из теории игр предполагала выбор оптимальной стратегии в условиях риска. Это ситуации, когда игрок знает вероятности наступления исходов и последствий для каждого решения. Совсем другая ситуация наступает, когда эти вероятности не известны, т.е. имеет место полная неопределённость в отношении возможности реализации состояния среды. В этом случае игру можно представить таким образом, что в ней имеется один игрок и некая действительность, называемая природой. Условия такой игры обычно представляется такой же платёжной матрицей, что и раньше, в которой строки представляют стратегии игрока, а столбцы – стратегии природы. В данном случае при выборе наилучшего решения обычно используют следующие критерии: 1. Максимаксный критерий, или критерий крайнего оптимизма – определяет альтернативу, которая максимизирует максимальный результат для каждой альтернативы, т.е. выбирается стратегия, которой соответствует
2. Максиминный критерий Вальда, или критерий крайнего пессимизма – определяет альтернативу, которая максимизирует минимальный результат для каждой альтернативы, т.е. выбирается стратегия, которой соответствует
3. Критерий минимаксного риска Сэвиджа. Согласно этому критерию выбирается стратегия, при которой величина риска
Здесь риск 4. Критерий оптимизма-пессимизма Гурвица рекомендует при выборе решения не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом. Согласно этому критерию стратегия выбирается из условия
Значение коэффициента пессимизма k выбирается исследователем между нулём и единицей из практических соображений. 5. Критерий безразличия Лапласа. В условиях полной неопределённости предполагается, что все возможные среды (природы) равновероятны. Этот критерий выявляет альтернативу с максимальным средним результатом, т.е.
Если известны вероятности реализации для всех состояний среды, можно определить ожидаемую стоимостную оценку EMV для каждой альтернативы. Один из наиболее распространённых критериев выбора альтернативы – максимальная EMV. Для каждой альтернативы ожидаемая стоимостная оценка EMV есть сумма всевозможных выигрышей для этой альтернативы, умноженных на вероятности реализаций этих выигрышей:
EMV( Максимальная EMV в случае равных вероятностей совпадает с критерием безразличия Лапласа. Проиллюстрируем эти положения на следующем примере, реализованном в модуле Decision Analysis/Decision Tables. На рисунке 4.6 просчитаны почти все описываемые критерии, кроме критерия минимаксного риска Сэвиджа, который рассчитан на рисунке 4.7. Из обозначений строк и столбцов очевидны те или иные критерии. Так, например, в столбце EMV (рисунок 4.6) внизу показана максимальная EMV. Кроме того, внизу этого рисунка прописаны значения конкретных критериев и указано, на каких альтернативах они реализованы.
Рисунок 4.6 – Окно отчёта о решении задачи анализа решений
Рисунок 4.7 – Окно отчёта о вычислении критерия минимаксного риска Сэвиджа На рисунке 4.7 показаны расчёты критерия минимаксного риска Сэвиджа (он равен 4 и реализован второй альтернативой).
Задания к выполнению лабораторной работы №4 Необходимо выполнить анализ всех задач, описанных в этом разделе. Исходную информацию для выполнения лабораторной работы возьмёте из задания по транспортной задаче. Игра должна быть 4х4. Матрица транспортных расходов – это три стратегии игрока А. Четвёртую стратегию этого игрока составит строка потребностей (последняя строка, не включённая в матрицу транспортных расходов). Для решения задачи графическим методов выберите две активные стратегии игрока А с минимальными частотами. Для анализа игры с природой возьмите эту же платёжную матрицу.
Лабораторная работа №5 Системы массового обслуживания
Общие сведения Существует широкий класс задач, с которыми приходится постоянно сталкиваться в повседневной и хозяйственной деятельности, где имеют место процессы, приводящие к задержкам в обслуживании и очередям. Системы, в которых протекают указанные процессы, получили название систем массового обслуживания (МО), а математическим описанием или разработкой математических моделей процессов, протекающих в них, занимается теория МО. В процессе изучения очередей сначала необходимо обращать внимание на следующие основные её компоненты: входящий поток требований, каналы обслуживания, наличие очереди и выходящий поток. Эти составляющие не требуют разъяснения, за исключением дисциплины очереди. Последнее – это просто правило обслуживания. В дальнейшем мы будем рассматривать правило: первый пришёл, первый обслуживается. Системы МО связаны с двумя видами издержек: издержки обслуживания, увеличивающиеся при повышении уровня обслуживания, и издержки, связанные с ожиданием, уменьшающиеся с увеличением уровня обслуживания. Как известно, существует точка минимума общих издержек системы МО.
Определение оптимального уровня обслуживания, минимизирующего суммарные издержки системы МО, и является одной из основных задач при разработке и эксплуатации систем МО.
|
||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.179.210 (0.007 с.) |

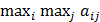 .
. .
. в наихудших условиях минимальна, т.е. равна
в наихудших условиях минимальна, т.е. равна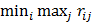 .
.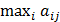 ) –
) – 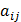 .
. + (1 – k)
+ (1 – k) 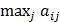 }.
}. .
.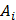 ) =
) = 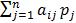 .
.