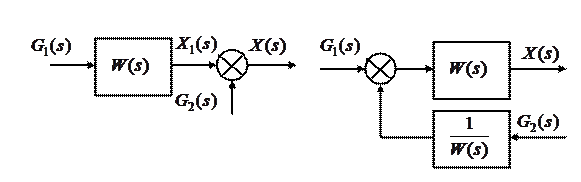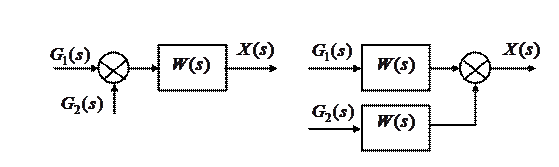Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы анализа и синтеза сарСодержание книги
Поиск на нашем сайте
Ряды и интегралы Фурье Гармонический анализ
В теории и практике автоматического регулирования часто встречаются процессы, которые могут рассматриваться как периодические. Функция f (t) называется периодической функцией, если при некотором постоянном числе Т>0, выполняется равенство
где Т – период функции; n – любое целое число, положительное или отрицательное, а аргумент t принимаем значения из области определения функции. Периодическая функция f (t) cпериодом Т обладает свойством, состоящем в том, что
Косинусоидальный (или синусоидальный) гармонический колебательный процесс
является примером простейшей периодической функции. Эта функция называется гармонической с амплитудой А, угловой частотой w и начальной фазой j. Нетрудно убедиться, что гармоника имеет период T=2p/w. В самом деле
т.е. равенство (1) выполняется. Сложение гармоник с различными частотами w, 2w, 3w, кратными наименьшей из них w приводит к образованию периодической функции с периодом T=2p/w равным периоду первой гармоники с частотой w. Эта функция отличается от гармоник. Каждое из слагаемых функции может характеризовать, например, косинусоидальное колебание, однако их сумма не является косинусоидой. Ещё более будет отличаться от косинусоиды график функции
представляющий собой сумму бесконечного ряда. В дальнейшем приращение частоты при переходе от гармоники с номером k к соседней с номером k +1 будем обозначать Dw. Тогда частоту первой гармоники также следует обозначить Dw, т.е. Dw = 2p/T, где T – период функции f(t). Тогда
Общий член ряда (3) Ak cos(k Dw t-jk) – называется k –й гармоникой, частота k –й гармоники k Dw, кратна частоте первой гармоники Dw. Всякую ли заданную периодическую функцию f(t) можно представить в виде суммы гармонических составляющих, т. е. произвести её тригонометрическое разложение. Как найти неизвестные параметры каждой из гармоник разложения. Покажем, что периодические функции, принадлежащие весьма обширному классу функций, могут быть представлены в виде (3). Допускается существование нулевой гармоники А0. Функцию f(t) с периодом Т можно записать в виде:
Если учесть, что
и ввести обозначения Аkcosjk=ak; Аksinjk=bk; A0=a0/2, то
и (4) можно записать в более удобном виде:
Периодическая функция f(t), имеющая период Т, оказывается разложенной по косинусам и синусам углов, кратных углу Dw t. Если период функции f(t) T=2p, то Dw= 2p/T=1, тогда
Пусть функция f(t) имеет период, равный 2p, ипринадлежитк классу функций, для которых разложение существует. Определим неизвестные постоянные коэффициенты разложения (6) a0, ak, bk (k=1,2,…). Предварительно отметим свойство семейства функций 1, cos t, sin t, cos 2t, sin 2t … cos nt, sin nt…, состоящее в том, что интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину 2p равен нулю независимо от выбора нижнего предела интегрирования – свойство ортогональности на интервале длиной 2p. Найдём коэффициент a0. Предполагая, что ряд (6) является равномерно сходящимся, проинтегрируем этот ряд почленно от - p до + p.
Заменим интеграл от бесконечной суммы, суммой интегралов от отдельных слагаемых (это возможно благодаря равномерной сходимости ряда (6)), тогда
т.к. все интегралы под знаком суммы равны нулю. Откуда
Определим коэффициенты ak и bk. Для этого умножим обе части (6) на cos(nt), где n – целое положительное число, и проинтегрируем в пределах от -p до p
Первое слагаемое в правой части, а также те, в которых n ≠ k, из – за ортогональности семейства, обращаются в ноль т.е.
Следовательно
Аналогично, умножая (6) на sin(nt), после интегрирования получим
Формулы (7),(8) и (9) позволяют по заданной f(t) c периодом 2π найти коэффициенты разложения этой функции в тригонометрический ряд (6) называемый рядом Фурье. Коэффициенты ak и bk называют коэффициентами Фурье. Если функция f(t) четная на интервале (-π; π), то произведение f(t)cos(kt) представляет собой четную функцию, а f(t)sin(kt) – нечетную. В этом случае bk=0, а коэффициенты a0 и ak определяются по формулам
Если функция f(t) нечетная на интервале (-π; π), то f(t)cos(kt)- нечетная функция, а f(t)sin(kt) – четная. В этом случае a0=0, ak=0, а bk может быть определен по формуле
В формулах (7) –(9) интегрирование производилось на интервале (-π; π). Однако результат не изменится, если проводить интегрирование на каком либо другом интервале длиной 2π, например на интервале (0; 2π) Зная ak и bk легко определить амплитуду и начальную фазу k –й гармоники
Совокупность операций, в результате которых могут быть определены гармоники периодической функции f(t), называется гармоническим анализом. Пример. Разложить на сумму гармонических составляющих прямоугольную волну, определяемую функцией:
Полагая, что заданная функция допускает разложение её в ряд Фурье, определим коэффициенты a0, ak и bk. Т.к. f(t) – нечетная, то a0=ak=0. Определим коэффициент bk, применяя формулу(12):
Амплитуда первой гармоники A1=4a/π, а частота ∆ω=1*(1/c), амплитуда второй равна нулю, третьей A3=4a/3π, а частота 3∆ω=3*(1/c) и.т.д. Значения начальных фаз для всех гармоник разложения φk=π/2, arctg(bk/ak)=arctg ∞=π/2. Пусть функция f(t) задана на интервале (-π; π) и допускает разложение в ряд Фурье. Это значит, что ряд (6) с коэффициентами, определенными по (7) –(9) сходятся к f(t). При этом f(t) может быть непериодической. Разложение подобной функции в ряд Фурье на интервале (-π; π) означает, что f(t) периодически продолжена вне интервала (-π; π) на всю ось 0t. На интервале (-π; π) эта новая функция совпадает с f(t). Ряд Фурье для непериодической функции f(t) заданной в интервале (-π; π) совпадает с рядом Фурье для функции периодически продолженной на всю ось 0t. Вопросы сходимости не рассматриваем. Результаты разложения на сумму гармонических составляющих функции f(t), имеющей период 2π, распространим на периодические функции с периодом отличным от 2π.Разложим в тригонометрический ряд функцию f(t) периода Т. Опуская выкладки, получим (вводя новую переменную
где
Запишем тригонометричесеий ряд (5) в комплексной форме. Используя формулу Эйлера
получим
Введём обозначения:
Обозначив С0=a0/2, получим для функции f(t), заданной в интервале (-T/2, T/2), ряд Фурье (5) в комплексной форме:
Здесь, как и ранее ∆ω=2π/T – частота первой гармоники сk – комплексные коэффициенты разложения f(t) в раз. ejk∆ωt - комплексная гармоника. Так как 2ck=ak-jbk , то, принимая во внимание, что комплексное число Z может быть представлено в виде: Z=r ejφ, и равенство (13) найдём:
Величину Ck=2ck называют комплексной амплитудой k – ой гармоники. Очевидно, что Ak=2│ck│. Формулу (17) удобнее записывать в виде:
где F(jk∆ω)=(2ck/∆ω)π (*) – относительная комплексная амплитуда k – ой гармоники. Неизвестные коэффициенты в разложении (17) определяются по формуле:
а F(jk∆ω) с учётом (*)
т.к. ∆ω=2π/T. В формуле (17) суммирование производится как по положительным, так и по отрицательным значениям k. Таким образом, комплексная форма ряда Фурье допускает существование и положительных и отрицательных частот ω=k∆ω. Однако после суммирования комплексных слагаемых останутся несколько вещественные величины, так как комплексные коэффициенты ck и c-k являются сопряженными.
Понятие о спектрах Совокупности коэффициентов ak,bk разложения периодической функции f(t) в ряд Фурье называют частотными спектрами этой функции. Из формул (8) и (9) видно, что ak= ak(k); bk= bk(k), если f(t) имеет период 2π, а если период Т, то ak= ak(k∆ω); bk= bk(k∆ω). Здесь частота первой гармоники ∆ω=2π/T, т.е. спектры являются функциями, зависящими от номера гармоники k, как независящей переменной. Графически частотные спектры изображают в виде отрезков длины ak,bk, проведённых перпендикулярно к оси, на которую наносим значения k или k∆ω. Т.к. k=1,2,… частотные спектры имеют дискретный (разрывный) характер, расстояние между отдельными линиями спектра в общем случае равно ∆ω, а при t=2π – единице. Совокупность комплексных чисел Сk=2сk, определяемых для f(t) c периодом Т формулой (19) называется комплексным амплитудным частотным спектром. Совокупность величин Ak= Ak(k∆ω) и φk=φk(k∆ω) (k=1,2,3…) называются соответственно амплитудным и фазовым частотными спектрами периодической функции f(t). Ранее отмечалось, что k может быть как положительным, так и отрицательным. Поэтому график спектров Аk и φk имеет смысл и при положительных, и при отрицательных частотах ω=k∆ω Аk=2│сk│, φk= -arg сk=arctg (bk/ak). Отсюда получим, что A+│k│= A -│k│, φ+│k│= -φ -│k│, т.е. амплитудный частотный спектр является четно-симметричной, а фазовый частотный спектр – нечетно-симметричной функцией частоты ω. Таким образом, при определении спектров часто достаточно изобразить лишь половину спектра при k∆ω > 0. Пример. Изобразить частотные спектры периодической функции
Заданная функция имеет значения коэф.(см. пред. пр.) ak=0; bk=0 при четном k; bk=4a/(πk) – при нечетном k.
Отметим, что между периодическими функциями и их частотными спектрами существует взаимнооднозначное соответствие: f(t) определяет ее частотные спектры и, наоборот, зная частотные спектры, можно указать какой периодической функции они принадлежат. Благодаря этому соответствию в ряде задач техники оказывается удобным операции над периодическими процессами заменять операциями над частотными спектрами, характеризующими эти процессы.
ИНТЕГРАЛ ФУРЬЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ Прямое и обратное преобразование Фурье Совокупность операций, позволяющих по заданной функции f(t) находить соответствующую ей спектральную характеристику F(iω) называется преобразованием Фурье:
Символически формулу (1)будем записывать в виде
Интеграл в правой части (1) как и ранее понимается в смысле главного значения, т.е.
Равенство (1) устанавливает связь между функцией f(t), аргументом которой служит t, и ей соответствующей комплексной функцией F(iω), имеющей в качестве аргумента частоту ω. Формула интеграла Фурье
позволяет от известной функции F(iω) определить соответствующую ей функцию f(t). На этом основании формулу (3) называют обратным преобразованием Фурье. Символически будем записывать
В ряде задач автоматического регулирования функция f(t) характеризует процесс, имеющий место лишь начиная с некоторого момента времени t, который можно принять за нулевой. В этом случае f(t) ≡ 0 при t < 0 (1) принимает вид
Преобразование (5) называется прямым односторонним преобразованием Фурье. Обратное преобразование Фурье, соответствующее прямому одностороннему преобразованию, остается двусторонним по переменной ω и дается равенством
При t= 0, значение правой части (6) равно при t < 0, f(t) ≡ 0
СВЯЗЬ ПРЕОБРАЗОВАНИЙ ФУРЬЕ И ЛАПЛАСА Формула
прямого преобразования Лапласа может рассматриваться как результат определенным образом построенного обобщения одностороннего преобразования Фурье. Пусть, например, f(t) удовлетворяет условиям Дирихле в интервале 0 ≤ t < ∞, причем f(t) ≡ 0 при t< 0. Как известно, преобразование Фурье может быть применено к функциям f(t), для которых интеграл Для того чтобы иметь возможность подобную функцию f(t) преобразовать по Фурье, предварительно ее надо умножить на e-ct где вещественное число С>C0 выбрано таким образом, чтобы интеграл Значение С0 для каждой функции f(t) является вполне определенным. Используя формулу прямого одностороннего преобразования Фурье, будем преобразовывать по Фурье не f(t), а f(t)e-ct, удовлетворяющую условиям применения этого преобразования.
Введя новую комплексную переменную S=c+jω, получим Это выражение представляет собой формулу прямого преобразования Лапласа. Таким образом, преобразование Лапласа является результатом распространения преобразования Фурье на функции, которые, удовлетворяя условиям Дирехле в интервале 0<t< ∞, не удовлетворяют в этом интервале условию абсолютной интегрируемости. Если F(jω) спектральная х – тика f(t), то функция F(S) комплексной переменой S является спектральной характеристикой затухающей функции времени f(t)e-ct. Рассмотрим формулу обратного преобразования Фурье:
Заменим в правой и левой частях этого равенства f(t) на f(t)e-ct, получим:
Учитывая, что S=e + jω, dω=dS/j, найдём
Это равенство является формулой обратного преобразования Лапласа, т.е. обратное преобразование Лапласа может рассматриваться как развитие обратного преобразования Фурье. Ранее отмечалось, что представление функции в виде интеграла Фурье соответствует представлению функции в виде суммы бесконечно большого числа гармоник с бесконечно малыми амплитудами, причем частоты гармоник отличаются друг от друга бесконечно мало. Аналогично этому представлению f(t) в виде (*) соответствует представлению этой функции в виде бесконечно большого числа бесконечно малых составляющих, являющихся колебаниями с бесконечно малыми амплитудами, затухающих по экспоненциальному закону. Свойства преобразования Фурье аналогичны свойствам преобразования Лапласа. Пусть воздействие g(t) = A1sin ω1t, Типовые динамические звенья И их характеристики Типовыми динамическими звеньями называются звенья, описываемые дифференциальными уравнениями не выше второго порядка. Такие звенья классифицируются в зависимости от вида левой и правой частей их дифференциальных уравнений. Их можно разделить на три группы: - позиционные; - интегрирующие; - дифференцирующие. Каждая из этих групп, в свою очередь содержит несколько типовых звеньев. Рассмотрим наиболее часто встречающиеся на практике типовые динамические звенья и определим для каждого из них основные характеристики: - дифференциальное уравнение; - передаточную функцию; - переходную функцию: - импульсную переходную функцию (функцию веса); - амплитудно-фазовую частотную характеристику; - амплитудную частотную характеристику; - фазовую частотную характеристику; - логарифмические частотные характеристики (ЛАЧХ, ЛФЧХ). 1. Позиционные звенья – такие звенья, для которых в установившемся режиме характерна линейная зависимость между входной и выходной величинами. Эти звенья описываются линейным диф. уравнением вида: D(p)x(t)=b0g(t) (1) где D(p) – многочлен не выше второго порядка. При постоянном входном сигнале выходная величина устойчивых позиционных звеньев с течением времени стремится к постоянному значению. а) Безинерционное (идеальное) усилительное звено. Звено, как в установившемся, так и в переходном режиме описывается уравнением вида:
где k – коэффициент передачи (усиления). Передаточная функция звена Переходная функция Весовая функция Частотные характеристики: АФХ
АЧХ
ФЧХ
ЛАЧХ и ЛФЧХ
б) Апериодическое звено Любое устройство, описываемое дифференциальным уравнением вида (a0p+ a1)x(t)=b0g(t) Деля на a1, получим (Tp+1)x(t)=kg(t), где
Передаточная функция звена
Определим переходную характеристику с помощью преобразования Лапласа. Т.к.
Теоретически переходной процесс длится бесконечно долго. Практически для этого звена под временем переходного процесса понимается наименьший промежуток времени, по истечении которого выполняется неравенство:
где [обычно Учитывая, что
АФХ Построим АФХ в координатах Re и Im функции
Умножим числитель и знаменатель на сопряженный множитель
Обозначим
Исключим из них
Добавляя и вычитая из правой части
АЧХ

ФЧХ
Логарифмическая частотная характеристика ЛАЧХ апериодического звена
При При Характеристики Заметим, что при
Частота, на которой сопрягаются эти характеристики, называется сопрягающей частотой. Ломаная линия с уравнением
Если построить реальную ЛАЧХ по точкам, можно убедится, что максимальное отличие от асимптотической имеет место на сопрягающей частоте. Оно не велико (меньше 3 дб). Практически можно считать, что реальная и асимптотическая ЛАЧХ совпадают и ограничиваться построением асимптотических характеристик. Фазовая логарифмическая характеристика ЛФЧХ
строится по точкам.
в) Колебательное звено Звено любой физической природы (маятник, колебательный контур и т.д.), описываемое диф. уравнением вида: (a0p2+ a1p+a2)x(t)=b0g(t) при определенных соотношениях параметров a1 называется колебательным звеном. Разделив на a2, получим: (Т2p2+2 где
Передаточная функция колебательного звена
Характеристическое уравнение
имеет комплексные корни:
где Выражение для переходной функции найдем используя обратное преобразование Лапласа:
Разложив на простые дроби, в соответствии с таблицей оригиналов и изображений, получим
где
Продифференцировав полученное выражение, определим функцию веса:
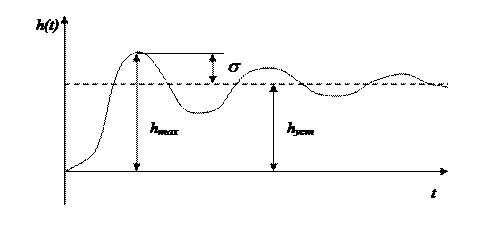
Переходной процесс рассматриваемого звена носит характер затухающих по экспоненте колебаний.
Практически важно определить время затухания переходного процесса tп – начальный промежуток времени, по истечении которого выполняется неравенство
где Иногда полезно знать максимальное отклонение
Как видно величина перерегулирования зависит только от относительного коэффициента затухания (коэффициента демпфирования) Амплитудно - фазовая характеристика, соответствующая передаточной функции будет
Имея такую характеристику, легко определить значения амплитуды и начальной фазы вынужденных колебаний х(t) на выходе системы при наличии на ее входе гармонического управляющего воздействия Амплитудно-частотная характеристика имеет вид:
а фазовая частотная характеристика
Найдем
Следовательно, экстремум будет существовать на частоте
При
Подставив
Чем меньше значение
Выражение для логарифмической АЧХ имеет вид:
Асимптотическая ЛАЧХ будет состоять из двух участков:
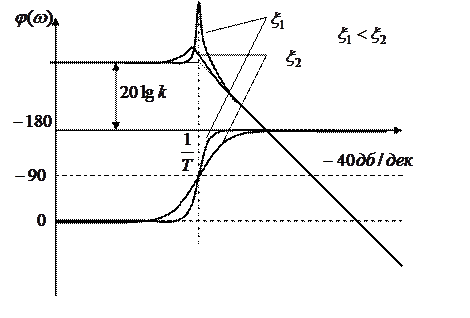
При
Все его характеристики могут быть получены из характеристик колебательного звена при Интегрирующие звенья Интегрирующими называются звенья, работа которых описывается диф. уравнением вида
В них имеет место в установившемся режиме линейная зависимость между входной величиной и производной выходной величины или другими словами выходная величина пропорциональна интегралу по времени от входной величины. а) Идеальное интегрирующее звено. Диф. уравнение
Передаточная функция
Временные характеристики определяются: - переходная функция - весовая функция Амплитудно-фазовая характеристика
ЛАЧХ
Если если
б) Интерпретирующее звено с замедлением (реальное инт. звено) описывается уравнением Передаточная функция в) Изодромное звено. Описывается диф. уравнением Передаточная функция 3. Дифференцирующие звенья – называются такие, у которых в установившемся режиме выходная величина пропорциональна производной по времени от входной. а) Идеальное дифференцирующее звено. Диф. уравнение Передаточная функция Переходная функция Весовая функция Амплитудно-фазовая характеристика АЧХ АФХ ЛАЧХ

Если б) Дифференцирующее звено с замедлением описывается диф. уравнением Передаточная функция
Структурные схемы Правила преобразования структурных схем
1. Последовательное соединение звеньев
Для n звеньев
2. Параллельное соединение звеньев
Для n звеньев
4. Соединение звеньев с обратной связью.
Если 4. Перемещение элементов суммирования а) на вход звена (против хода сигнала)
б) на выход звена (по ходу сигнала)
5. Перемещение точек съема а) на выход звена (по ходу сигнала)
б) на вход звена (против хода сигнала)
6. Перестановка а) элементо
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.68.167 (0.015 с.) |













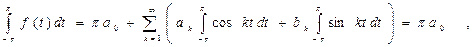

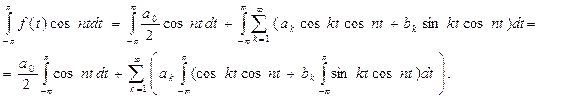

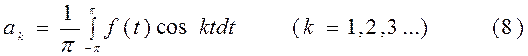









 и переходя к старой)
и переходя к старой)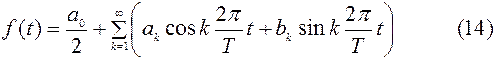










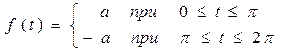



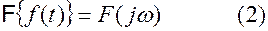



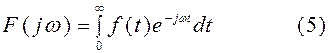
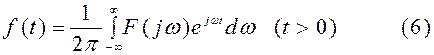
 ;
;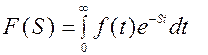
 существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе процессов в автоматических системах, например 1(t), Asin(ω t), Acos(ω t), eαt при α >0, t и др.
существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе процессов в автоматических системах, например 1(t), Asin(ω t), Acos(ω t), eαt при α >0, t и др. был бы сходящимся.
был бы сходящимся.
 .
.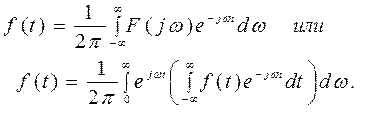
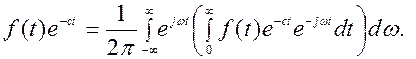

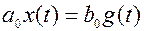 или
или  ,
, .
.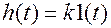 ;
;




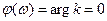



 - постоянная времени звена,
- постоянная времени звена, - коэффициент передачи звена.
- коэффициент передачи звена. .
. ,
, ,
, или
или .
.
 ,
, - наперед заданное положительное число
- наперед заданное положительное число (0,01 – 0,05) k. ], или tп= (3 – 5)T.
(0,01 – 0,05) k. ], или tп= (3 – 5)T. , найдем, что
, найдем, что - функция веса.
- функция веса.
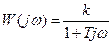 .
. . Для этого представим
. Для этого представим  .
. .
. ;
;  .
. :
: , подставив в
, подставив в 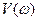 , получим:
, получим: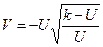 , или возводя в квадрат
, или возводя в квадрат .
. , получим
, получим , или
, или - окружность с центром, смещенным на
- окружность с центром, смещенным на 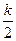 по действительной оси и радиусом
по действительной оси и радиусом 

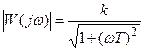
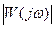
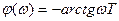

 .
. ,
, 
 .
. и
и  называют низкочастотной и высокочастотной асимптотами.
называют низкочастотной и высокочастотной асимптотами.
 .
. при
при  и
и при
при 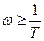 называется асимптотической ЛАЧХ апериодического звена.
называется асимптотической ЛАЧХ апериодического звена.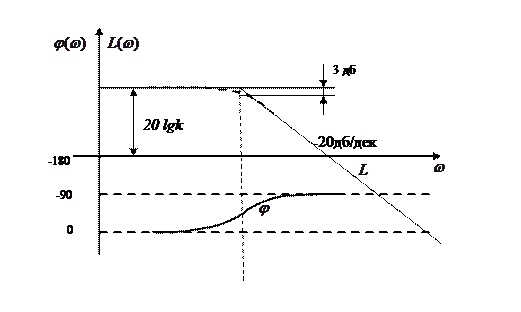

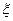 Тp+1)x(t)=kg(t),
Тp+1)x(t)=kg(t), постоянная времени,
постоянная времени, ;
; ;
;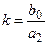 .
.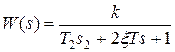 .
. =0
=0 ,
,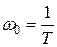 .
. .
. ,
, ;
; .
. .
.
 ,
, - наперед заданное положительное число. Более грубо можно считать, что процесс закончится тогда, когда затухли «сжимающие» его экспоненты.
- наперед заданное положительное число. Более грубо можно считать, что процесс закончится тогда, когда затухли «сжимающие» его экспоненты. или величину перерегулирования
или величину перерегулирования  . Их можно вычислить по формуле
. Их можно вычислить по формуле :
: .
. .
. .
.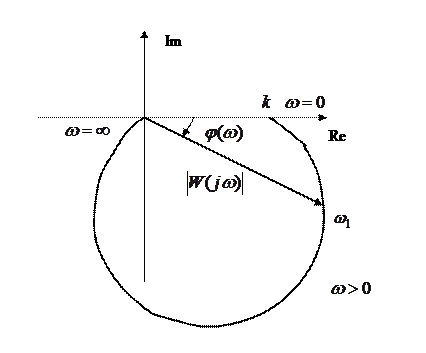
 .
. ,
, .
. , для чего определим минимум подкоренного выражения в знаменателе и, приравняв его к нулю, получим
, для чего определим минимум подкоренного выражения в знаменателе и, приравняв его к нулю, получим .
. - резонансная частота.
- резонансная частота. частота
частота  совпадает с собственной частотой
совпадает с собственной частотой  колебаний системы.
колебаний системы. .
. .
.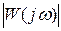 max. При
max. При  ,
, 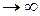 .
.

 .
. при
при  ;
;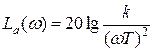 при
при 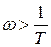 ;
;
 .
. .
.






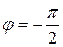
 - прямая линия.
- прямая линия. , то
, то 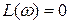 ;
; , то
, то 


 может рассматриваться как последовательное соединение идеального интегрирующего и апериодического звеньев.
может рассматриваться как последовательное соединение идеального интегрирующего и апериодического звеньев. .
.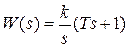 , где
, где  может рассматриваться как параллельное соединение интегрирующего и пропорционального звеньев
может рассматриваться как параллельное соединение интегрирующего и пропорционального звеньев 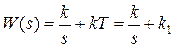 .
.


 .
.


 - прямая линия.
- прямая линия.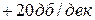


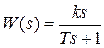 может рассматриваться как последовательное соединение идеального дифференцирующего и апериодического звеньев
может рассматриваться как последовательное соединение идеального дифференцирующего и апериодического звеньев 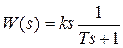 .
.
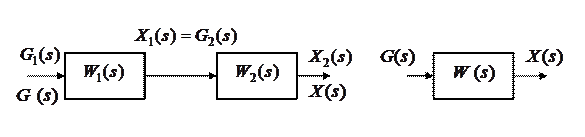


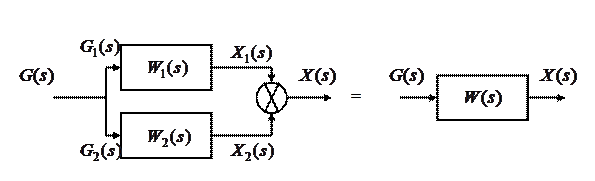

 .
.
 ;
;
 - передаточная функция прямой цепи;
- передаточная функция прямой цепи;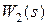 - передаточная функция обратной связи.
- передаточная функция обратной связи. ;
; ;
;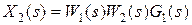 ;
;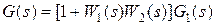 ;
;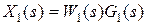 ;
;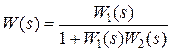 .
.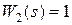 , то говорят, что в системе существует единичная обратная связь.
, то говорят, что в системе существует единичная обратная связь.