
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между частотными и временными характеристиками линейной системы.Содержание книги
Поиск на нашем сайте
Пусть имеется предварительно невозбужденная (с нулевыми начальными условиями) линейная автоматическая система, причем ее амплитудно-фазовая частотная характеристика по отношению к управляющему воздействию есть Ф(jw).
Предположим, что в момент времени t=0 на вход системы подано управляющее воздействие в виде дельта-фуекции, т.е. g(t)=d(t). Реакция системы на дельта-функцию называется импульсной переходной функцией и обычно обозначается k(t). Импульсная переходная функция является одной из временных характеристик автоматической системы. Т.к.
или учитывая, что
Следовательно, амплитудно-фазовая частотная характеристика системы является спектральной характеристикой импульсной переходной функции. Справедлива также формула обратного преобразования Фурье.
Реакция x(t) системы на воздействие в виде единичной ступенчатой функции 1(t) называется переходной функцией системы и обозначается h(t). Учитывая, что
Найдем спектральную характеристику переходной функции
или т.к. h(t)=0 при t<0. Переходная функция является временной характеристикой системы. Она может быть определена с помощью обратного преобразования Фурье.
Т.к. умножению на jw соответствует операция дифференцирования во временной области, можно записать
Используя фильтрующие свойства дельта-функций второе слагаемое при Ф(j0) ¹¥ равно нулю
Откуда
Т.е.
Пусть теперь на вход автоматической системы в момент времени t=0 поступает управляющее воздействие g(t) общего вида найдем реакцию x(t) системы на это воздействие. Для этого воспользуемся теоремой о свертывании функций в вещественной области.
и равенство
Формула (8) является временным аналогом формулы (*), характеризующей спектральные (частотные) соотношения в автоматической системе. Интеграл в правой части называется интегралом Дюамеля. Рассмотрим детальнее роль импульсной переходной функции k(t-t). Управляющее воздействие g(t), поступающее в автоматическую систему, можно аппроксимировать ступенчатой ломаной с бесконечно большим числом ступеней и бесконечно малым шагом каждой ступени.
Тогда возбуждение системы воздействием g(t) сводится к возбуждению системы непрерывной серией импульсов величиной g(t)dt. Реакция системы на единичный импульс в виде дельта-функции, приложенный к системе в момент времени t=t, известна и равна k(t-t). Очевидно, что реакция системы на импульс величиной g(t)dt, приложенный в тот же момент t=t есть k(t-t)g(t)dt. Реакция системы на всю совокупность импульсов, т.е. на g(t) определяется равенством
т.е. состоит из суммы реакций на каждый импульс в отдельности. Пусть t является моментом наблюдения за реакцией системы x(t), t-t - интервал времени между приложением к системе импульса g(t)dt и рассматриваемым (текущим) моментом t>t. Функция k(t-t) будет определять степень участия импульсов, приложенных к системе до рассматриваемого момента времени в образовании значения x(t) реакции системы в текущий момент времени t. Оно (влияние) зависит от характера импульсной переходной функции k(t-t) (см. реакции k1(t-t) и k2(t-t)). Следовательно, импульсная переходная функция как бы «взвешивает» роль каждого импульса, приложенного к системе в момент t=t, в образовании реакции системы в рассматриваемый момент времени t>t. По этой причине часто импульсную переходную функцию называют также весовой функцией. Кроме того, на основании свойств преобразования Фурье можно установить еще одно соответствие между импульсной переходной функцией k(t) и амплитудно-фазовой частотной характеристикой, а именно:
где а – положительная постоянная, независящая от t и Отсюда следует, что если k(t) растягивать (сжимать) вдоль оси времени t, то соответствующая ей амплитудно-частотная характеристика Пример. Определить АФХ и АЧХ линейной системы, если весовая функция этой системы
По (1) имеем
Весовой функции в виде бесконечно короткого импульса соответствует бесконечно широкая частотная характеристика.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.29 (0.006 с.) |


 ,
, ,
, при t<0, получим
при t<0, получим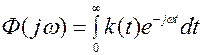 . (1)
. (1) (t>0). (2)
(t>0). (2)
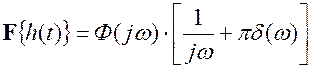 (3)
(3) , (4)
, (4) (t>0) (5)
(t>0) (5)
 ,
, (6)
(6) (7)
(7)
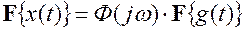 (*)
(*) (8)
(8)

 (9)
(9) .
. будет сжиматься (растягиваться) вдоль оси частот
будет сжиматься (растягиваться) вдоль оси частот  .
.
 .
.


