
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическая модель дискретного и интегрального полупроводникового диодаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основой полупроводникового диода является переход на границе двух слоев полупроводникового материала с различными типами проводимости. В качестве модели диода можно использовать модель Эберса-Молла для одиночного перехода:
С Д– сумма барьерной и диффузионной емкостей перехода, R Д– сопротивление утечки, r – объемное сопротивление тела базы, зависящее от геометрических размеров и степени легирования полупроводника, I Д– управляемый напряжением на переходе источник тока Ток источника подчиняется закону:
где I 0 – ток насыщения перехода, обусловленный тепловой генерацией неосновных носителей в слоях полупроводника, А и М – эмпирические коэффициенты, Т – абсолютная температура В электрической модели дискретного диода необходимо учесть наличие индуктивностей выводов анода L А и катода L К, емкости корпуса и контактов C К и C П. Интегральный диод обычно представляет собой полную структуру биполярного транзистора, изолированную от подложки и используемую в диодном включении.При этом рабочим является лишь один из переходов. Варианты представления интегрального диода через полную структуру биполярного транзистора Электрическая модель МДП-транзистора МДП-транзистор в отличие от биполярного является четырехполюсным прибором(выводы – исток, сток, затвор, подложка).
Структура электрической модели МДП-транзистора аналогична модели линейных приращений биполярного транзистора.
Элементы С К, R К учитывают инерционные свойства носителей в канале; межэлектродные емкости C’ ЗИи C’ ЗС обусловлены перекрытием областей стока и истока областью затвора, а C” ЗИ, C ЗС– влиянием частей канала, находящихся под управляющим воздействием затвора; r ЗИ и r ЗС– сопротивления утечек; r С и r И– объемные сопротивления областей стока и истока; R СП, R ИП– сопротивление р-области между подложкой, стоком и истоком.
Электрическая модель операционного усилителя. Операционный усилитель (ОУ) – интегральный элемент, предназначенный для реализации математических функций над аналоговыми сигналами. Для него характерны: наличие двух входов («дифференциальный» вход), большой коэффициент усиления (30... 120 дБ), зависимость коэффициента усиления от частоты, небольшое смещение выходного напряжения относительно нуля при нулевом напряжении на дифференциальном входе усилителя, высокие значения входных сопротивлений, низкие значения выходного сопротивления, наличие небольших входных токов смещения. В локальной модели (идеального ОУ) не учитываются частотная зависимость коэффициента передачи, смещение выходного напряжения, входные токи смещения
Здесь резистор R 1 отражает конечное входное сопротивление между двумя дифференциальными входами и 1и и 2;управляемый источник напряжения Ui=k(u 1 -u 2 ) – усилительные свойства; резистор R2 –конечную нагрузочную способность операционного усилителя (зависимость выходного сигнала от сопротивления нагрузки усилителя). Возможный вариант глобальной макромодели ОУ для линейного режима работы в диапазоне частот показан ниже: U см – источник, моделирующий напряжение смещения, I 1 и I 2 – источники тока, моделирующие входные токи смещения. Управляемый источник тока I 3 = sU c комплексным сопротивлением нагрузки R 3 –C 3 моделирует частотную зависимость коэффициента передачи ОУ. Усложнением этого сопротивления можно обеспечить практически любую частотную характеристику коэффициента передачи. Если это сопротивление нагрузки будет нелинейным, то можно будет учесть и нелинейность амплитудной передаточной характеристики ОУ. Источник напряжения Ui=kU 3, управляемый напряжением U 3, характеризует усилительные свойства, а резистор R 4 и конденсатор C 4–нагрузочную способность ОУ. Математические модели во временной и частотной области. Целесообразность проведения анализа во временной и частотной областях. Связь между выходными параметрами при моделировании во временной и в частотной области В зависимости от того, являются ли фазовые переменные функциями времени t или комплексной частоты p=j ω, различают математические модели во временной и в частотной областях. При моделировании во временной области компонентные уравнения математической модели связывают мгновенные значения напряжений и токов, действующих на базовом элементе. Данные модели наиболее удобны для анализа переходных процессов, при моделировании статического режима, моделировании нелинейных устройств. При моделировании в частотной области компонентные уравнения связывают комплексные амплитуды напряжений и токов, действующих на базовом элементе. Суть метода заключается в том, что в установившемся режиме в любой электрической цепи при синусоидальном воздействии напряжения и токи могут быть представлены в виде суммы синусоидальных составляющих основной (ω) и высших (2ω, 3ω, …) гармонических составляющих. Наиболее часто такой подход (спектральный анализ) применяется при анализе радиочастотных трактов, в которых протекают такие периодические синусоидальные токи. При формировании системы уравнений математической модели обычно используют операторную форму записи компонентных уравнений для базовых элементов электрических моделей. Рассмотрим связь между некоторыми выходными параметрами при моделировании во временной и в частотной области. Если k (j ω)– комплексный коэффициент передачи цепи, то частотная k (j ω)и импульсная g (t)характеристики цепи связаны между собой парой преобразований Фурье (ПФ):
Если используются не аналоговые, а дискретные сигналы, то данные соотношения применяются не в виде интегралов, а в виде дискретных сумм (дискретные преобразования Фурье, ДПФ). При подаче на вход устройства произвольного входного сигнала x вх (t) выходной сигнал х вых (t) во временной области можно найти с помощью интеграла свертки (Дюамеля):
Свертке сигналов во временной области соответствует перемножение спектров в частотной области:
где X ВХ(j ω) и X ВЫХ(j ω) – спектры входного и выходного сигналов. Достоинство частотных методов анализа по сравнению с временными – высокое быстродействие, возможность анализа устойчивости по совокупному анализу амплитудно- и фазочастотных характеристик.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.239 (0.01 с.) |


 ,
,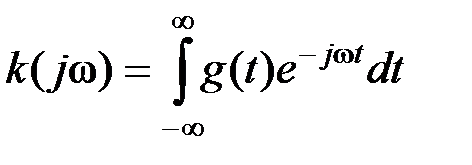

 .
. ,
,


