
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пакеты программ автоматизированного проектирования РЭС.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Системы программ, предназначенные для автоматизированного проектирования РЭС, часто принято называть EDA-приложениями. Их можно разделить на две основные группы: системы схемотехнического проектирования и конструкторского проектирования РЭС. Кроме основных групп пакетов программ, в САПР РЭС широко используются различные вспомогательные пакеты: математические пакеты, базы данных, графические и текстовые редакторы, электронные таблицы. Для моделирования электрических схем используются различные языки описания схем. Наиболее распространенными являются алгоритмические языки Spice и VHDL. Пакет программ Spice (PSpice) описывает встроенные математические модели типовых компонентов: биполярные транзисторы, МДП-транзисторы, полевые транзисторы с управляющим p-n – переходом, арсенид-галлиевые полевые транзисторы, диоды, резисторы, конденсаторы, индуктивности, независимые источники напряжения и тока, линии задержки, ключи, управляемые источники, операционные усилители, компараторы. Язык VHDL Описывает алгоритмы через последовательность операторов присваивания и принятия решений. Используется для проектирования цифровых устройств. Наиболее распространенные системы программ, предназначенные для автоматизированного проектирования устройств промышленной электроники и их характеристики приведены в таблице.
20.Классификация частотно-избирательных фильтров. Передаточная функция реализуемого фильтра. АЧХ идеального и реального ФНЧ. Групповое время задержки фильтра и его связь с ФЧХ. ФЧХ идеального и реального ФНЧ. Основные требования при проектировании фильтров. Электрический фильтр – это частотно-избирательное устройство, изменяющее амплитудный или фазовый спектр сигнала. Характеристику частотно-избирательного фильтра в частотной области принято описывать при помощи передаточной функции W(p).
АЧХ фильтра – это модуль передаточной функции | W (j w)|, а фазочастотная характеристика (ФЧХ) – это аргумент передаточной функции j (w). АЧХ определяет фильтрующие свойства по амплитуде: составляющие сигнала, имеющие различные частоты, будут ослабляться фильтром в разной степени. ФЧХ характеризует фильтрующие свойства по фазе: составляющие сигнала, имеющие различные частоты, будут сдвигаться фильтром по фазе в разной степени. По виду амплитудно-частотной характеристики (АЧХ) различают 4 основных вида фильтров - фильтр нижних частот (ФНЧ) – пропускает НЧ от 0 Гц и задерживает ВЧ; - фильтр верхних частот (ФВЧ) – пропускает ВЧ и задерживает НЧ; - полосно-пропускающий фильтр (ППФ) – пропускает полосу частот и подавляет частоты выше и ниже этой полосы; - полосно-заграждающий фильтр (ПЗФ) – подавляет определенную полосу частот и пропускает частоты выше и ниже этой полосы. Для возможности анализа формы АЧХ в широких диапазонах изменения коэффициентов передачи и частот, АЧХ, как правило, представляют в логарифмическом масштабе
Также возможно представление АЧХ в виде затухания для нормированной АЧХ (имеющей единичный коэффициент передачи в полосе пропускания):
ЛАЧХ фильтра нижних частот: 1. 0¸wс – полоса пропускания; 2.wс¸ w1 – переходная область; 3.w1¸ ¥ – полоса задерживания Групповое время задержки (время замедления)
характеризует фазовые искажения, вносимые фильтром на разных частотах (время задержки фильтром максимума передаваемой энергии). С точки зрения ФЧХ идеальным считается фильтр, имеющий постоянное групповое время задержки в полосе пропускания, и, следовательно, линейную ФЧХ (этому условию удовлетворяют ФНЧ Бесселя). Такие фильтры не вносят в сигнал линейных искажений ФЧХ идеального и реального фильтров нижних частот
Проектирование фильтра производится с учетом одного или нескольких из следующих требований: 1) форма АЧХ должна обеспечивать частотную избирательность (требуемое отношение «сигнал/помеха» на выходе фильтра); 2) в случае, сигнал широкополосный (т.е. содержит набор гармоник), форма ФЧХ в полосе пропускания должна быть близка к линейной; 3) время установления выходного сигнала фильтра должно быть минимальным, а переходный процесс – иметь малую амплитуду перерегулирований; 4) аппаратные затраты на реализацию схемы фильтра должны быть минимальны. При проектировании фильтров, в зависимости от задачи, стремятся к наилучшему приближению (аппроксимации) идеальных частотных характеристик (АЧХ либо ФЧХ). Следует отметить, что одновременная аппроксимация и АЧХ, и ФЧХ невозможно.
ФНЧ Баттерворта Фильтр нижних частот Баттерворта обладает монотонной АЧХ, никогда не возрастающей с увеличением частоты, наиболее близкой к идеальной горизонтали на низких частотах (рис. 5.6). Частота среза ωс фильтра Баттерворта определяется по относительному уровню A 1= –3дБ (т.е. по уровню затухания 3дБ) Рис. 5.6. ЛАЧХ ФНЧ Баттерворта: n – порядок фильтра; Для нормированного фильтра, т.е. при значении wc, равном 1 рад/cек, передаточную функцию ФНЧ Баттерворта можно записать в виде произведения сомножителей для n = 2, 4, 6...
или для n = 1, 3, 5... В обоих случаях коэффициенты задаются при b 0 = 1 и для
АЧХ ФНЧ Баттерворта описывается следующим выражением: где k – коэффициент усиления; n – порядок фильтра. Увеличение порядка n ФНЧ приближает АЧХ к идеальной. Для низкочастотного диапазона АЧХ фильтра Баттерворта наилучшим образом аппроксимирует идеальную АЧХ ФНЧ. ЛАЧХ ФНЧ Баттерворта описывается функцией:
Для нормированной АЧХ k = 1, отсюда:
Найдем порядок n тр ФНЧ Баттерворта, требуемый для реализации заданной АЧХ. Для этого необходимо выразить значение n из логарифмической частотной характеристики:
где А.ч.х. фильтра Баттерворта наиболее плоская в районе частоты w=0, по сравнению с а.ч.х. любого другого полиномиального фильтра. Вследствие этого ее называют максимально плоской. Следовательно, для диапазона низких частот (полосы пропускания) данный фильтр наилучшим образом отображает идеальную характеристику. Однако в полосе частот, находящихся около wс и в полосе задержания, а.ч.х. фильтра Баттерворта заметно уступает характеристике фильтра Чебышева.
ФНЧ Чебышева ФНЧ Чебышева представляет собой оптимальный полиномиальный фильтр. он обеспечивает минимальную ширину переходной области АЧХ и превосходит в этом отношении фильтр Баттерворта. Фильтр Чебышева содержит колебания (пульсации) передаточной функции в полосе пропускания и обладает монотонной характеристикой в полосе задержания. Рис. 5.7. ЛАЧХ ФНЧ Чебышева АЧХ ФНЧ Чебышева описывается следующим выражением: где ε и k – постоянные числа, Сn(x) – полином Величиной ε определяется неравномерность коэффициента передачи вполосе пропускания (см. рис. 5.8):
Рис. 5.8. ЛАЧХ ФНЧ Чебышева: а) – нечетного порядка; б) – четного порядка. Для нечетного n частота среза ωсопределяется по уровню затухания АЧХ α 1 дБ (или Dk раз), а для четного n – по уровню 0 дБ(или 1 раз) относительно коэффициента усиления на постоянном токе k. ЛАЧХ ФНЧ Чебышева описывается функцией:
Для нормированной АЧХ (k = 1):
Для нахождения требуемого порядка n тр ФНЧ Чебышева запишем:
Разделив второе уравнение системы на первое, извлекаем квадратный корень из правой и левой частей:
А.ч.х. достигает своего наибольшего значения, равного К в тех точках, в которых Сn = 0. Поскольку эти точки распределены в полосе пропускания, то характеристика фильтра Чебышева содержит пульсации в полосе пропускания и монотонна в полосе задержания. Размах этих пульсаций определяет параметр e, а их число - порядок фильтра n. Коэффициент усиления фильтра Чебышева определяется значением К. Фильтр Чебышева часто называют равноволновым фильтром. Для К=1 размах пульсаций Rw составляет:
Размах пульсаций, или неравномерность в полосе пропускания выражается в децибелах (дБ) следующим образом:
Значение a используют как характеристику фильтра Чебышева.
Характеристики ФНЧ Бесселя Фильтр нижних частот Бесселя отличается от других фильтров тем, что имеет оптимальную фазочастотную характеристику с точки зрения неискаженной передачи сигнала в полосе пропускания. Проходящий через фильтр сигнал не изменит своей формы, если все гармоники сигнала будут задерживаться в фильтре на одно и то же время, т.е. ФЧХ фильтра будет иметь линейный характер. Фильтр Бесселя обеспечивает наилучшее приближение реальной ФЧХ к идеальной линейной зависимости, но имеет меньший наклон АЧХ в полосе подавления и переходной области, чем фильтры Баттерворта и Чебышева. Частота среза фильтра Бесселя определяется не по АЧХ, а по излому характеристики группового времени задержки τ(ω), пример которой изображен на рис. 5.9. Рис. 5.9. Характеристика группового времени задержки Передаточная функция фильтра Бесселя n -го порядка имеет вид: где k – коэффициент усиления фильтра на постоянном токе; Bn(p) – полином Бесселя:
где bm – числовые коэффициенты полинома Бесселя; n – порядок фильтра, определяемый числом реактивных элементов; ωc – частота среза ФНЧ Бесселя – предельная частота, на которой сохраняется постоянное время замедления, вносимое фильтром. Частотная характеристика времени замедления фильтра Бесселя τ(ω) в диапазоне частот от 0 до ωcмонотонно спадает от значения на частоте ω = 0, равного τ(0) ≈ 1/ωc, до значения на частоте ω = ωс при увеличении порядка фильтра время замедления приближается к постоянному значению. При этом обеспечиваются условия неискаженной передачи сигнала сложной формы. АЧХ фильтра Бесселя уступает характеристикам фильтров Баттерворта и Чебышева, т.к. имеет меньшую крутизну спада в переходной частотной области. Для заданного времени замедления τ(0)в полосе пропускания можно приблизительно найти частоту среза ωcФНЧ и частоту по уровню затухания АЧХ 3 дБ (для n ≥ 3):
Инверсный ФНЧ Чебышева Инверсный и эллиптический ФНЧ Чебышева относятся к классу неполиномиальных фильтров, т.е. тех, которые описываются передаточной функцией общего вида:
при ненулевых коэффициентах не только знаменателя, но и числителя. Инверсный фильтр Чебышева имеет АЧХ, которая монотонна в полосе пропускания и содержит пульсации в полосе задерживания. На рис. 5.11 показана ЛАЧХ инверсного фильтра Чебышева 4-го порядка. Рис. 5.11 ЛАЧХ инверсного фильтра Чебышева 4-го порядка АЧХ инверсного ФНЧ Чебышева описывается выражением: где ε – постоянное число, Сn(x) – полином Чебышева первого рода степени n:
Величиной εопределяется неравномерность коэффициента передачи вполосе задерживания (ω ≥ ω1):
Размах пульсаций составляет
Отсюда можно определить величину ε:
Частота среза ωсдля инверсного фильтра Чебышева любого порядкаопределяется по уровню затухания 3 дБ. Для определения требуемого порядка n тр инверсного ФНЧ Чебышева
С учетом ɛ получим: Анализ последнего выражения показывает,что требуемый порядок инверсного ФНЧ Чебышева примерно требуемому порядку ФНЧ Чебышева, имеющего допустимое затухание в полосе пропускания α1 = 3 дБ. Эллиптический фильтр Чебышева имеет АЧХ, содержащую пульсации как в полосе пропускания, так и в полосе задерживания. АЧХ эллиптического ФНЧ Чебышева имеет самый крутой наклон на частотах выше ωс.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.243 (0.012 с.) |

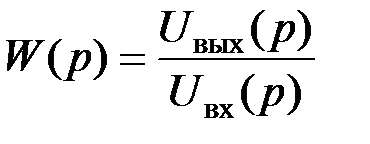
 , дБ.
, дБ. , дБ.
, дБ. .
. ,
, .
.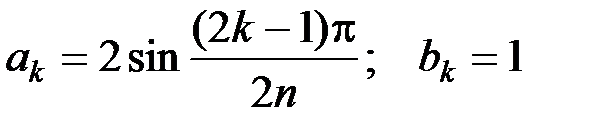 .
. ,
, .
.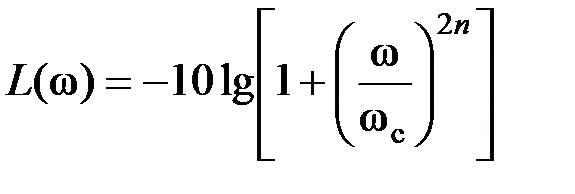 ,
, 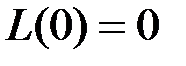 ,
,  .
. ;
;  ;
; ;
;  ;
;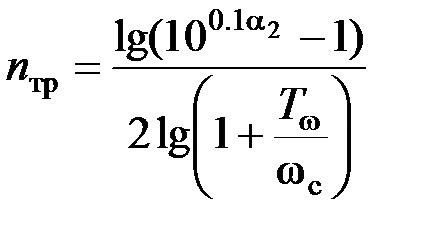 ,
, – нормированная ширина переходной области АЧХ.
– нормированная ширина переходной области АЧХ. ,
, .
. .
. .
. .
. .
. ;
; 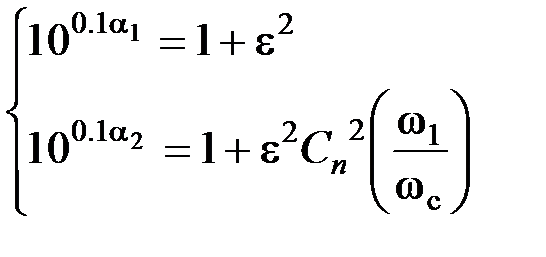
 .
. ;
; 
 .
. .
. ,
,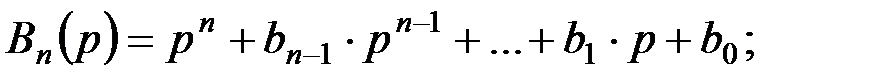
 ,
,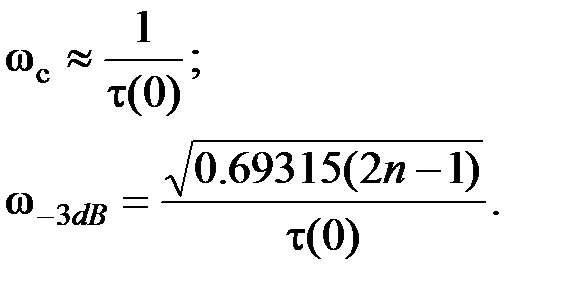

 ,
,
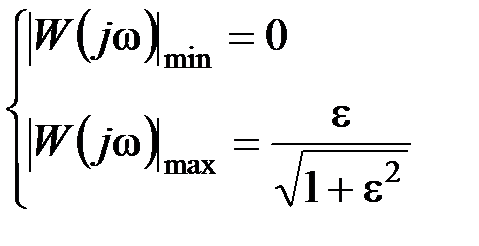 .
.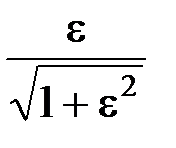 , или в логарифмическом масштабе для затухания:
, или в логарифмическом масштабе для затухания:


 .
.


