
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схемная реализация активных фильтровСодержание книги
Поиск на нашем сайте
Схема активного фильтра 1-го порядка показана на рис. 5.26. Здесь и далее каждый пассивный элемент (резистор либо конденсатор), входящий в схему активного фильтра, условно обозначается комплексным сопротивлением z i. Путем замены данных сопротивлений на активные либо емкостные сопротивления, при сохранении топологии схемы, можно получить на ее основе различные типы фильтров. Рис. 5.26. Активный фильтр 1-го порядка ФНЧ: ФВЧ:
Рис. 5.27. Схемы фильтров 1-го порядка: а) – ФНЧ; б) – ФВЧ Передаточная функция схемы рис. 5.26 имеет вид:
С учетом (5.13) передаточная функция ФНЧ имеет вид:
Коэффициенты передаточной функции ФНЧ:
Схемные элементы выбираются из условий:
Регулировки схемы: коэффициент усиления задается изменением соотношения резисторов R 3 и R 2 (k → R 3/ R 2); частота среза задается изменением сопротивления R 1 (f c → R 1). В случае k =1 R 3 выбирается равным R 1, а R 2 – размыкается. С учетом (5.14) передаточная функция ФВЧ имеет вид:
Коэффициенты передаточной функции ФВЧ:
Схемные элементы выбираются из условий:
Регулировки схемы: частота среза задается изменением сопротивления R 1 (f c → R 1); коэффициент усиления задается изменением соотношения резисторов R 3 и R 2 (k → R 3/ R 2). В случае k =1 R 3 выбирается равным R 1, а R 2 – размыкается.
Схема Рауха (с МОС) Рис. 5.28. Схема Рауха Достоинство схемы – минимальное количество элементов
ФНЧ: ФВЧ: ППФ:
ФНЧ 2-го порядка:
Коэффициенты передаточной функции ФНЧ:
Схемные элементы выбираются из условий:
Регулировки схемы: f c → R 3; ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом:
Коэффициенты передаточной функции ФВЧ:
Схемные элементы выбираются из условий:
Регулировки схемы: f c → изменение R 1 и R 2 в равном процентном соотношении; Q → R 1 или R 2; k → С 1/ С 2. ППФ 2-го порядка с полиномиальным ФНЧ-прототипом:
Коэффициенты передаточной функции ППФ:
Схемные элементы выбираются из условий:
Регулировки схемы: f 0 → R 2 и R 3 (в равном процентном соотношении);
31. Схема Саллен-Ки (схема источника напряжения, управляемого напряжением): достоинства и недостатки. Реализация ФНЧ, ФВЧ, ППФ 2-го порядка.
Схема Саллен-Ки Достоинство схемы – высокое входное сопротивление. Недостаток – ограничения по добротности и коэффициенту усиления: Фильтры 2-го порядка на основе схемы Саллен-Ки
Передаточная функция ФНЧ 2-го порядка: .
Коэффициенты передаточной функции ФHЧ:
Учитывая условие симметрирования ОУ:
Передаточной функции ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом:
Коэффициенты передаточной функции ФВЧ:
Учитывая условие симметрирования ОУ:
Регулировки схемы: f c → R 1 и R 2 (в равном процентном соотношении); Передаточной функции ППФ 2-го порядка с полиномиальным ФНЧ-прототипом:
Принимая обозначение
Для удобства примем μ=2.Учитывая условие симметрирования, дополнение к системе имеет вид:
Схемные элементы выбираются из условий:
Регулировки схемы: f 0 → R 3;
32. Биквадратная схема: достоинства и недостатки. Реализация ФНЧ, ФВЧ, ППФ 2-го порядка.
Биквадратная схема Достоинства схемы: 1)высокая возможная добротность: 2) возможность построения звеньев, реализующих как полиномиальные (Баттерворта, Чебышева, Бесселя), так и неполиномиальные аппроксимации ЧХ (инверсный Чебышева, Кауэра). Недостатки: 1) высокие аппаратные затраты; 2) сложность настройки с учетом обеспечения точных соотношений номиналов резисторов.
а)
б)
в)
Передаточной функции полиномиального ФНЧ 2-го порядка:
Коэффициенты передаточной функции ФHЧ:
Схемные элементы выбираются из условий:
Регулировки схемы: f c → R 3; После подстановки в передаточную функцию (5.29) биквадратной схемы значений (5.26), при соблюдении в схеме рис. 5.35, б условия: Передаточная функция ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом:
Схемные элементы выбираются из условий:
Регулировки схемы: f c → R 3; Передаточной функции ППФ 2-го порядка с полиномиальным ФНЧ-прототипом:
Коэффициенты передаточной функции ППФ:
Схемные элементы выбираются из условий:
Регулировки схемы: f 0 → R 3;
33. Биквадратная схема: достоинства и недостатки. Реализация неполиномиального ФНЧ (инверсного Чебышева и Кауэра); ФВЧ, ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом.
Биквадратная схема Достоинства схемы: 1)высокая возможная добротность: 2) возможность построения звеньев, реализующих как полиномиальные (Баттерворта, Чебышева, Бесселя), так и неполиномиальные аппроксимации ЧХ (инверсный Чебышева, Кауэра). Недостатки: 1) высокие аппаратные затраты; 2) сложность настройки с учетом обеспечения точных соотношений номиналов резисторов.
.
Емкость C 1 выбирается из условия: Остальные схемные элементы выбираются из условий:
Регулировки схемы: максимальное подавление в полосе задерживания → R 4; f c → R 3;
Остальные схемные элементы выбираются из условий:
Регулировки схемы: максимальное подавление в полосе задерживания → R 4; f c → R 3;
Остальные схемные элементы выбираются из условий:
Если добротность Q и (или) коэффициент усиления k имеют значения более 10, то C 2 и R 7 должны выбираться таким образом, чтобы сохранился небольшой разброс значений сопротивлений схемы. Регулировки схемы: максимальное подавление в полосе задерживания → R 4; f 0 → R 3; Реализованные на биквадратной схеме неполиномиальный ФНЧ (инверсный Чебышева и Кауэра); ФВЧ, ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом имеют одну и ту же схемную реализацию, и один и тот же вид передаточной функции. Разница в их частотных характеристиках обусловлена различными соотношениями 4-х коэффициентов, входящих в передаточную функцию.
34. Требования к элементам активных фильтров. Порядок анализа схем активных фильтров в системе Micro-CAP(порядка нет, возможно ответ на стр 139) При проектировании схем активных фильтров необходимо учесть следующие особенности и требования: 1) При невысокой добротности (Q< 10) используются относительно простые схемы звеньев (Рауха, Саллен-Ки). При более высоких значениях Q применяются более сложные звенья (например, биквадратное звено). 2) Частотная характеристика фильтра не изменится, если значение всех сопротивлений умножить, а значение всех емкостей – поделить любое рациональное число > 0. 3) Для минимизации погрешностей от входных токов каждого ОУ, примененного в инвертирующем включении, между их неинвертирующими входами и земляной шиной необходимо включить резисторы (выполнить симметрирование ОУ). 4) Коэффициент усиления каждого примененного в схеме фильтра ОУ (с разомкнутой обратной связью) должен как минимум в 50 раз превышать коэффициент усиления фильтра в полосе пропускания. 5) Скорость нарастания выходного напряжения ОУ VU вых должна обеспечивать полный размах выходного напряжения в полосе пропускания: VU вых ≥ 2πfaUm, где Um – амплитуда выходного сигнала на частоте fa (наибольшей частоте, пропускаемой фильтром). 6) Чем выше порядок фильтра, тем выше требования к качеству применяемых резисторов и конденсаторов – требуется минимальный разброс номиналов и минимальный температурный коэффициент сопротивления (емкости). Ориентировочно для фильтров 4-го – 8-го порядков полагают, что наибольшее допустимое отклонение от номинала не должно превышать 1%. Не следует применять конденсаторы с номиналом менее 10 пФ, так как они имеют низкую точность.
35. Первичные преобразователи неэлектрических величин. Классификация параметрических и генераторных преобразователей неэлектрических величин. Первичные преобразователи неэлектрических величин делятся на два основных класса: параметрические и генераторные. В параметрических преобразователях выходной величиной является приращение параметров электрической цепи (R, L, M, C) и поэтому при их использовании всегда необходим дополнительный источник питания. В генераторных преобразователях выходной величиной являются ЭДС, ток или заряд, функционально связанные с измеряемой величиной. Классификация параметрических преобразователей неэлектрических величин показана на рис. 4.1, а классификация генераторных преобразователей неэлектрических величин – на рис. 4.2.
Рис. Классификация генераторных преобразователей неэлектрических величин
36. Термопреобразователи сопротивления: свойства, характеристики, способы моделирования в Micro-Cap. Термометром сопротивления (терморезистором) называется измерительный преобразователь, активное сопротивление которого изменяется с изменением температуры. Датчики температуры с терморезистором называются термометрами сопротивления, или термопреобразователями сопротивления (ТПС). В качестве материала для термометра сопротивления пригодны только те, физические и химические свойства которых не изменяются с течением времени в измеряемом диапазоне температур. Сопротивление такого материала должно хорошо воспроизводиться и с изменением температуры монотонно повышаться. Кроме того, такие внешние воздействия, как давление, влажность, коррозия, деформация, не должны влиять на сопротивление термометра. Сопротивление металлов в общем случае повышается с температурой. Показателем изменения сопротивления от температуры служит температурный коэффициент сопротивления (ТКС): где R 100 – сопротивление при t = 100 °С; R 0 – сопротивление при t = 0 °С; Δ t o = 100 °С, или характеристическое отношение сопротивлений:
а) б) Конструкции чувствительных элементов ТПС: а) – платинового; б) – медного Основные технические характеристики ТПС регламентируются ГОСТ 6651–94, в котором изменение сопротивления в функции температуры описывается номинальными статическими характеристиками (НСХ). При этом сопротивление ТПС определяется по формуле: Rt = Wt ∙ R 0. Аналитически каждая НСХ на определенных температурных отрезках может быть описана интерполяционным уравнением. Вид интерполяционного уравнения и его коэффициенты зависят от материала ТПС и характеристического отношения сопротивлений W 100.
Рис НСХ платинового ТПС c R 0 = 100 Ом, W 100 = 1,385 В обозначении ТПС указываются тип используемого материала Измерительный ток, вызывающий изменение сопротивления при 0 °С не более 0,1 % его номинального значения, в промышленных приборах, выбирается из ряда: 0,1; 0,2; 0,5; 1,0; 2,0; 3,0; 5,0; 10,0; 15,0; 20,0; 50,0 мА.
Разновидности конструктивного исполнения выводов ТПС: а – двухпроводная схема; б – трехпроводная схема; в – четырехпроводная схема Первый способ моделирования – при помощи линейного и квадратичного температурных коэффициентов модели резистора В текстовом окне MicroCAP при этом будет добавлена следующая строка: .MODEL R_PT_1 RES (R=1 LOT=0.05% TC1=3.9692E-3 TC2=-5.829E-7 T_ABS=400) Здесь LOT – допустимый разброс номинала ТПС класса допуска А, а T_ABS – абсолютная физическая температура компонента. При температуре анализа схемы, равной 27 0С, температура анализа данного компонента (ТПС) составит 400 0С. По указанному способу можно задавать модели ТПС не более чем с двумя температурными коэффициентами в интерполяционном уравнении. Второй способ моделирования – при помощи масштабного множителя сопротивления модели резистора (параметр «R»). Данным способом целесообразно задавать модель ТПС, если интерполяционное уравнение содержит более двух температурных коэффициентов. В текстовом окне MicroCAP при этом будет добавлена следующая строка: .MODEL R_Pt RES (R=1+400*(3.9692E-3 – 400*5.829E-7)LOT=0.05%) Здесь 400 – измеряемая температура.
37. Термисторы, моделирование в Micro-Cap. Тензорезисторы, моделирование в MicroCap. Емкостные преобразователи, моделирование в Micro-Cap. 1)Полупроводниковые термометры сопротивления (термисторы) изготавливаются из окислов меди, кобальта, магния, марганца и т. д. Заготовка размельчается, размалывается и испекается в виде столбика, шайбы или шарика и заливается стеклом. Термисторы отличаются от металлических термометров сопротивления гораздо меньшими габаритами и гораздо большими значениями ТКС. ТКС полупроводниковых терморезисторов, как правило, отрицателен.
,где А – постоянная, зависящая от материала и технологии, а также от формы термистора; В – коэффициент температурной чувствительности, имеющий размерность температуры. Номинальное сопротивление термисторов имеет широкий диапазон – ( 102…106) Ом. Кроме нелинейности, недостатком термисторов являются плохая воспроизводимость характеристик, что практически исключает взаимозаменяемость без подгонки. Пределы измерения для обычных термисторов составляют –100…+450 ºС. Благодаря малым размерам чувствительного элемента обеспечиваются хорошие динамические свойства при измерениях температуры. Основные области применения – химия, биология, медицина, системы температурной сигнализации.
Примеры характеристик термисторов
В Micro-CAP7 имеются модели термисторов, которые можно вставить в схему следующим путём: Component – Analog Library – Passive – Thermistor Эти модели, например С619, S861, заданы не параметрами, а в виде макромоделей (Subckts), поэтому перед их моделированием нужно ознакомиться с соответствующей технической документацией.Следует отметить, что в настоящее время довольно широко также распространены интегральные микросхемы температурных датчиков общего назначения с аналоговым выходом (AD590, AD592, AD22100, TMP35). Моделей данных ИМС в базовой версии Micro-CAP7 нет. Однако следует учитывать, что фирмы-производители наряду с новым изделием, как правило, выпускают и его программное макроописание (Spice text file), которое конвертируется средствами Micro-Cap в бинарную библиотеку, доступную для использования при моделировании. 2)Емкостный преобразователь представляет собой конденсатор, электрические параметры которого изменяются под действием входной величины. Конденсатор состоит из двух электродов, к которым подключены выводы. Пространство между электродами заполнено диэлектриком. При изменении взаимного положения электродов или при изменении диэлектрической проницаемости среды, заполняющей межэлектродное пространство, изменяется емкость конденсатора. В качестве емкостного преобразователя широко используется плоский конденсатор. Его емкость определяется выражением: Изменение любого из параметров δ, Q, ε r изменяет емкость конденсатора. Основным недостатком емкостных преобразователей является их малая емкость и высокое сопротивление. Для уменьшения последнего преобразователи питаются напряжением высокой частоты. Однако это обусловливает другой недостаток – сложность вторичных преобразователей. Недостатком также является и то, что результат измерения зависит от изменения параметров кабеля. Для уменьшения погрешности измерительную цепь и вторичный прибор располагают вблизи датчика. В Micro-CAP7 модель емкостного датчика задаётся как модель конденсатора. Если емкостной датчик может быть описан моделью плоского конденсатора, необходимо при вставке компонента задать величину номинала, равную 1 Ф (VALUE = 1), а в текстовом описании его модели в разделе <scale> записать формулу В емкостном преобразователе переменными величинами могут быть δ, Q (измерение перемещений), либо ε (измерение уровня). Соответственно одна из этих величин должна изменяться перед проведением анализа для пересчета текущего значения емкости преобразователя по формуле (1). Пример:.MODEL MOV_SEN CAP (C=1.00025*8.85e-12*0.01/5e-3 LOT=5%) Здесь ε r = 1,00025 (среда между обкладками – воздух); ε0 = 8,85·10-12 Ф/м; Q = 0,01м2 (пластины размером 0,1 x 0,1 м); δ = 5 мм, разброс значения емкости датчика = 5%. При моделировании изменения расстояния между пластинами от δ1 = 5 мм до δ2 = 20 мм, емкость датчика будет изменяться 17,7 пФ до 4,43 пФ. Тангенс угла потерь и электрическое сопротивление изоляции как параметры модели конденсатора Micro-Cap7 заданы быть не могут, но могут быть промоделированы посредством подключения внешних резисторов. 3)В основе принципа работы тензорезисторов лежит явление тензоэффекта, заключающееся в изменении сопротивления проводников и полупроводников при их механической деформации. Основной характеристикой чувствительности материала к механической деформации является коэффициент относительной тензочувствительности K Т (иногда в литературе обозначается как s):
где Δρ – изменение удельного сопротивления тензорезистора; Δ l – изменение длины проводника; Δ S – изменение сечения проводника. Как правило, для расчета сопротивления тензорезистора применяется следующая формула: Коэффициент тензочувствительности полупроводниковых тензорезисторов определяется в основном изменением электрического удельного сопротивления, в отличие от металлических тензорезисторов в значительной степени зависит от деформации, а также от температуры и достигает 150…200.
По конструкции тензорезисторы делятся на проволочные, фольговые и пленочные
Рис. 4.11. Конструкции тензорезисторов: а – проволочного; б – фольгового В Micro-CAP модель тензорезистора задаётся как модель резистора, имеющего номинальное сопротивление и ТКС того материала, из которого изготовлен тензорезистор. При этом необходимо при вставке компонента задать величину номинала, равную 1 Ом (VALUE = 1). Изменение эффективной длины моделируется соответствующим изменением масштабного множителя сопротивления (scale), рассчитываемого по формуле Пример:.MODEL R_PR RES (R=1+2*(0.15/6) LOT=5% TC1=5E-6) Здесь K Т= 2; Δ l = 0.15 мм; l = 6 мм, разброс номинала тензорезистора=5%, ТКС константана = 0,5·10-5 0С-1.
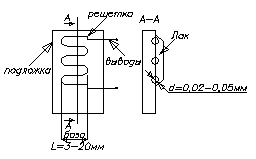
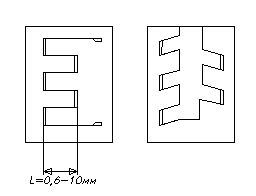
38. Индуктивные и трансф-е преобразователи, моделирование в Micro-Cap. Индуктивные преобразователи неэлектрических величин изменяют свою индуктивность или взаимную индуктивность в зависимости от положения, геометрических размеров и магн-го сопротивления элементов магн-ой цепи. Индуктивность обмоток, расположенных на магнитопроводе, наиболее сильно зависит от длины воздушного зазора d и площади поперечного сечения воздуш-го участка магнитопровода S: Рис.. Варианты индуктивных преобразователей: x – перемещение; S - площадь поперечного сечения воздушного участка магнитопровода; d – длина воздушного зазора магнитопровода
Рис. 4.18. а)Принцип работы дифференциального трансформаторного датчика перемещений, б)характеристика дифференциального трансформаторного датчика перемещений Вторичные обмотки включены встречно. При нейтральном (симметричном положении) сердечника напряжение на выходе равно нулю: Смещение сердечника относительно нейтрального положения приводит к появлению выходного напряжения, причём его фаза при переходе через нейтральное положение меняется на 1800. В MicroCAP7 модель индуктивности включена в раздел пассивных компонентов:
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 763; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.250 (0.012 с.) |

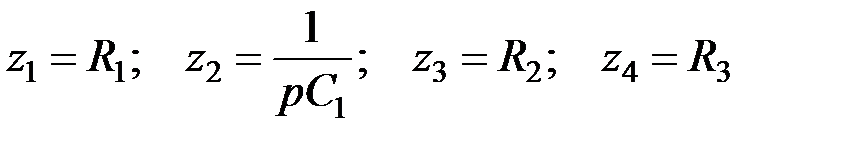 ; (5.13)
; (5.13)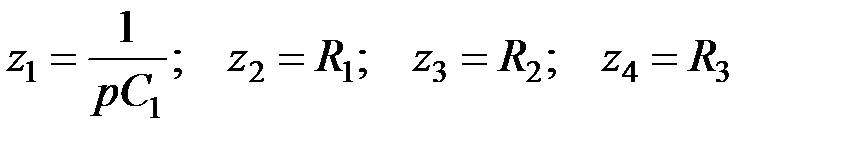 . (5.14)
. (5.14)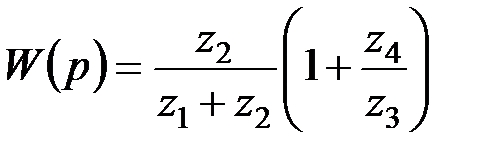 . (5.15)
. (5.15)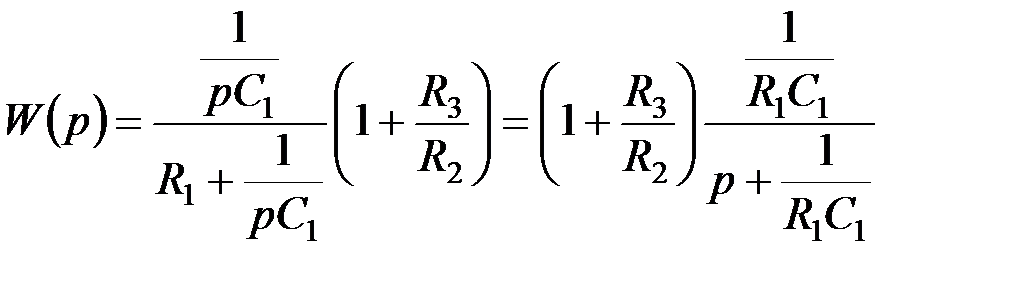 .
.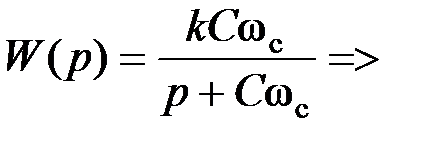
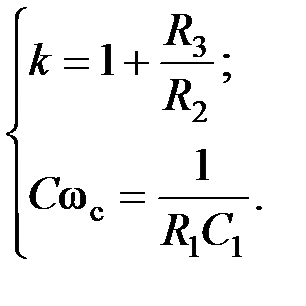
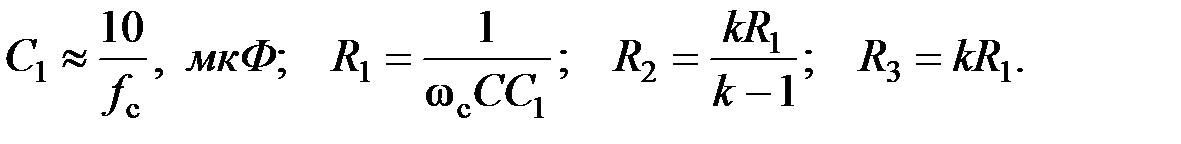
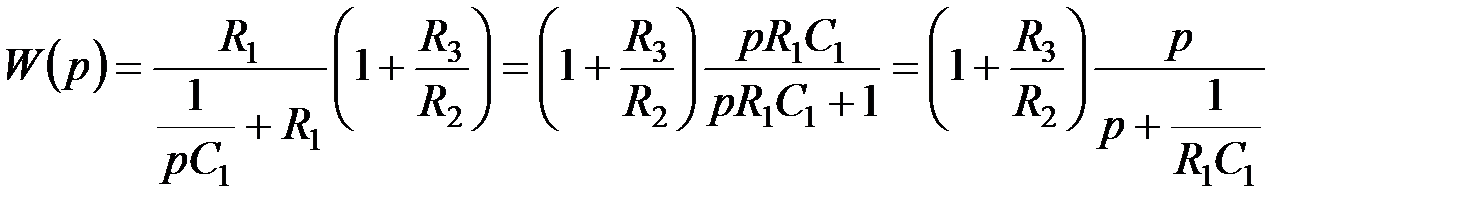 .
.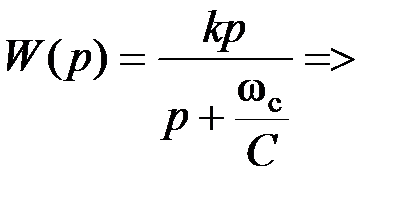
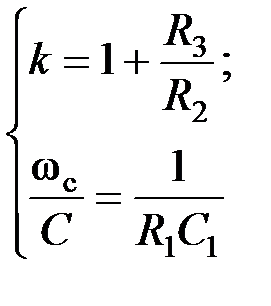
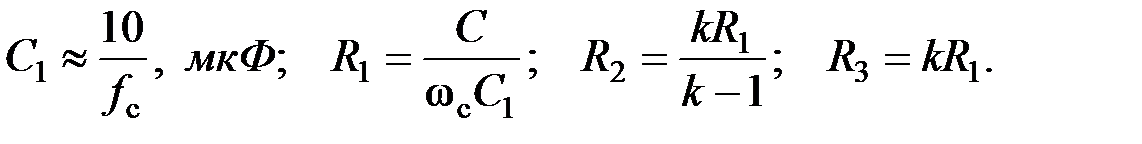
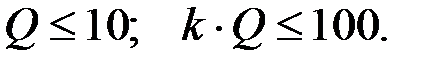
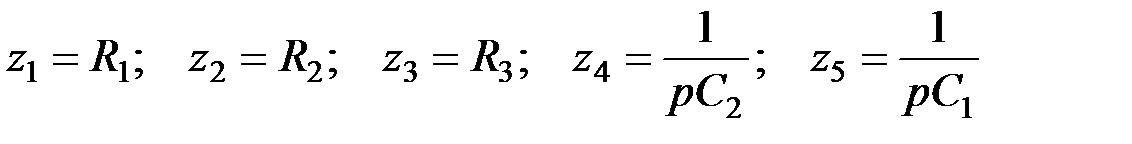 ; (5.16)
; (5.16)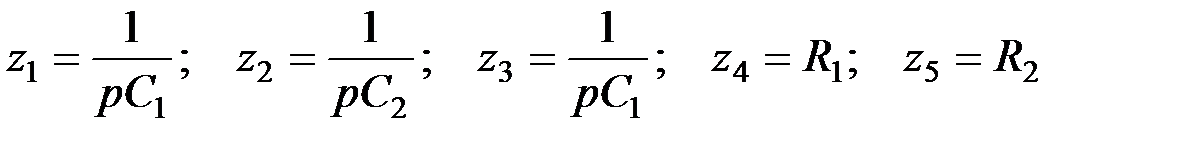 ; (5.17)
; (5.17)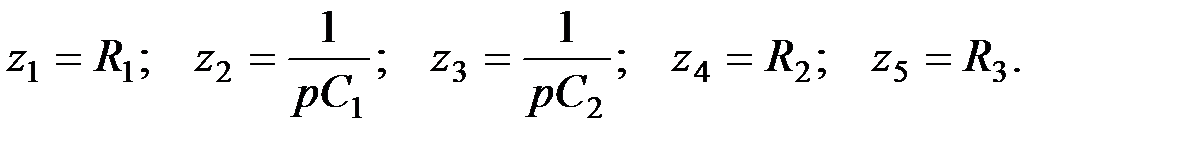 (5.18)
(5.18)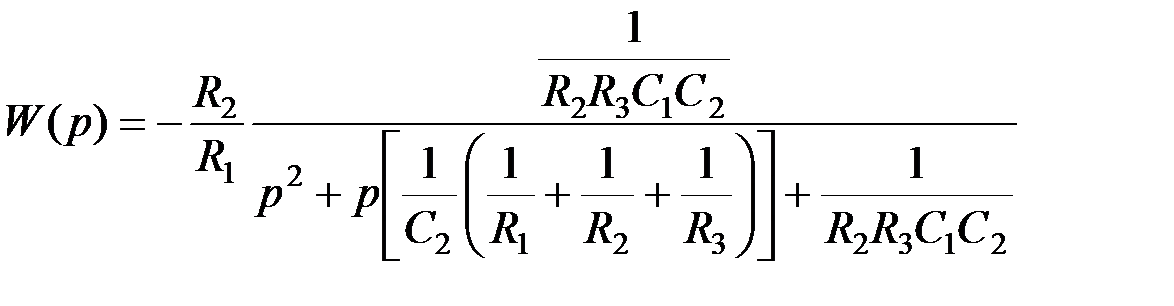 .
.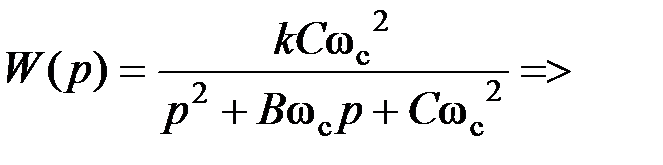
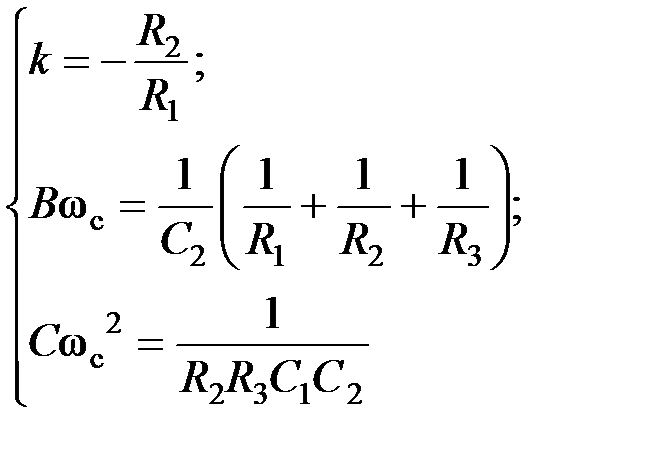
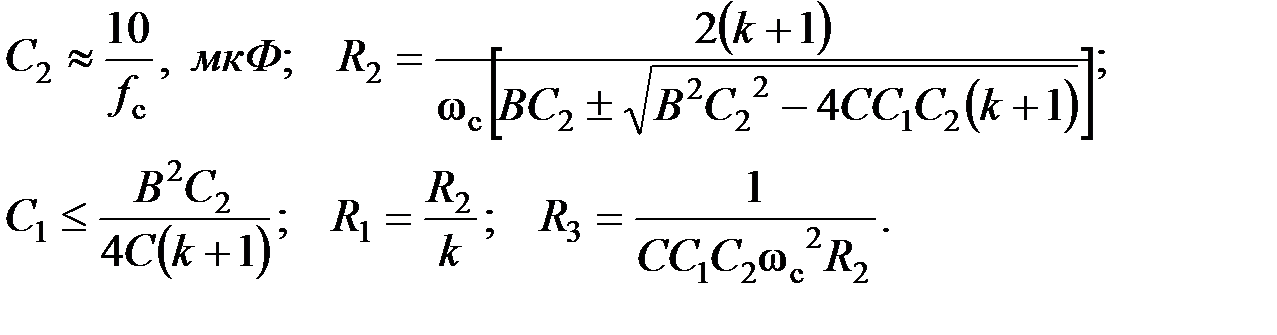
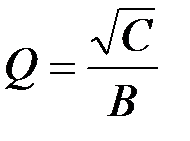 → R 1 или R 2; k → R 2/ R 1.
→ R 1 или R 2; k → R 2/ R 1.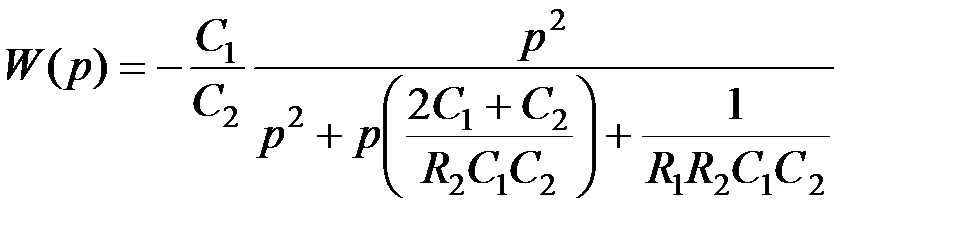 .
.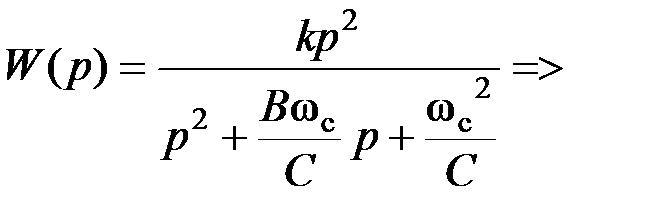
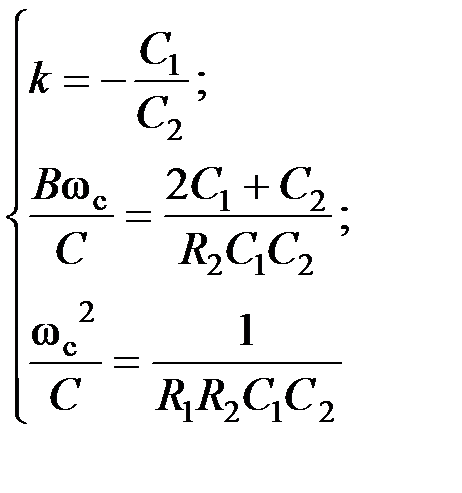
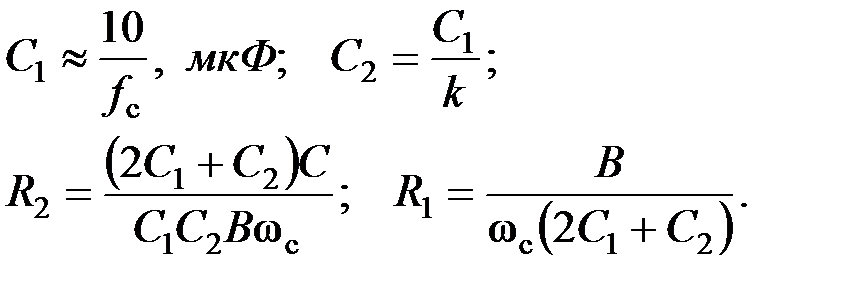
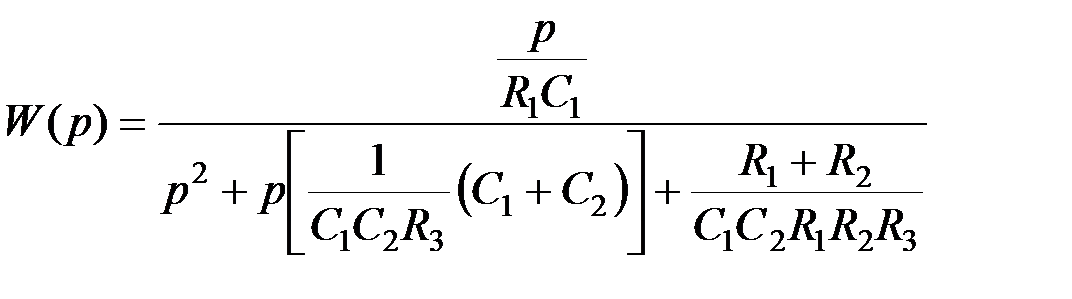 . (5.20)
. (5.20)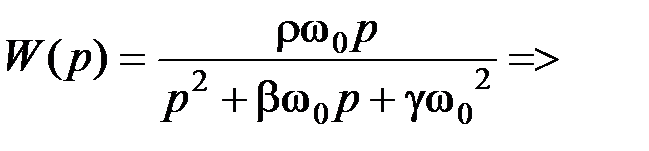
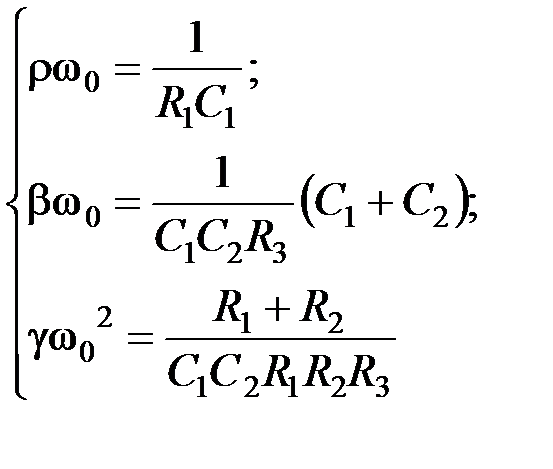
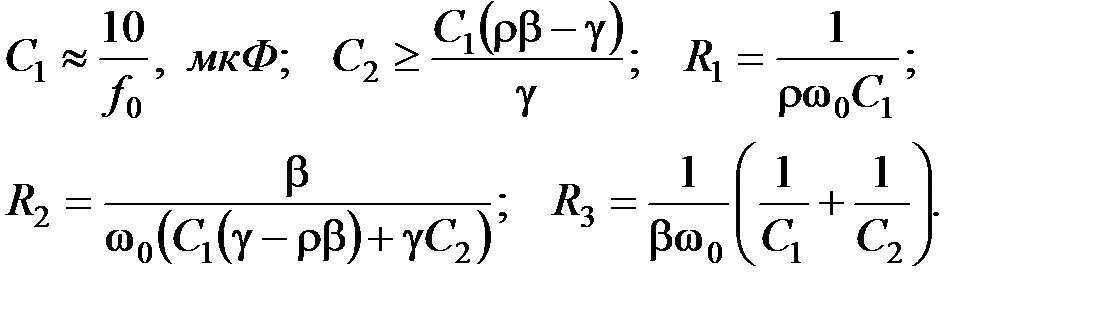
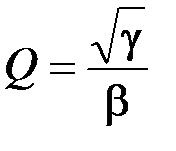 → R 2; k → R 1.
→ R 2; k → R 1.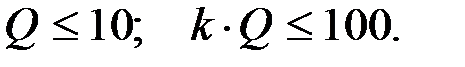
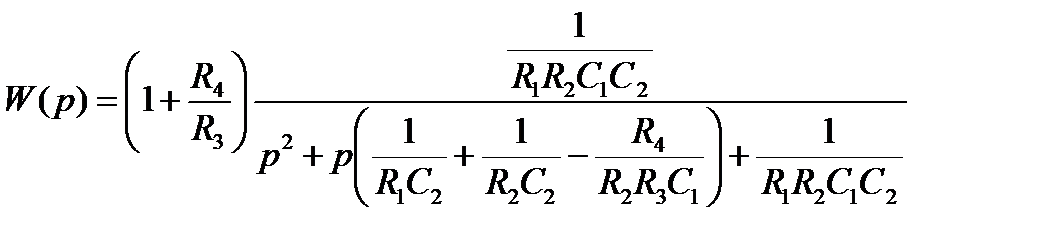
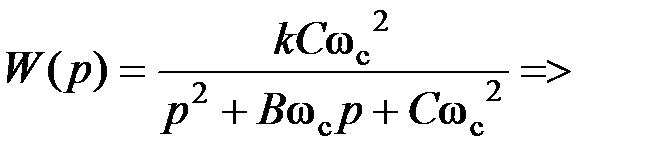
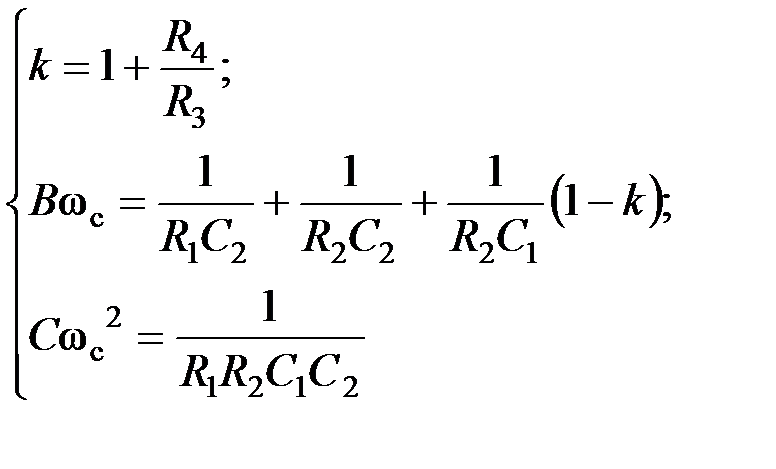
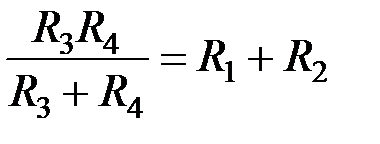 , получаем расчетные соотношения для элементов схемы:
, получаем расчетные соотношения для элементов схемы: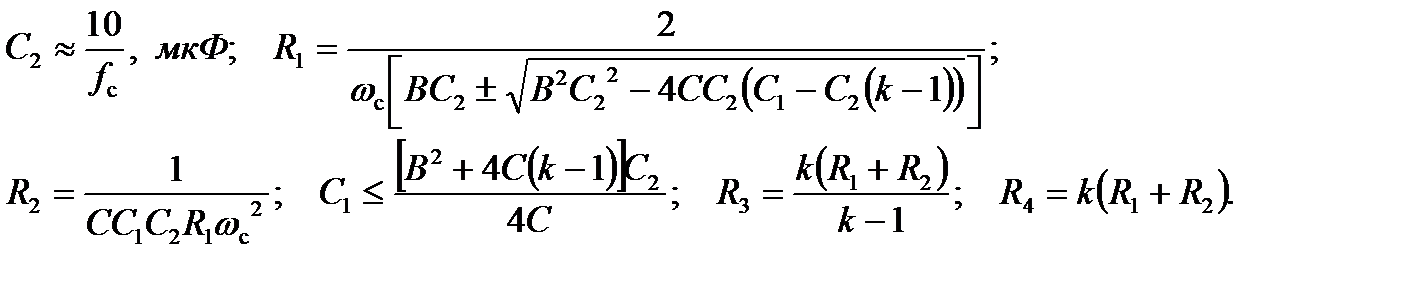 Регулировки схемы: f c → R 1 и R 2 (в равном процентном соотношении);
Регулировки схемы: f c → R 1 и R 2 (в равном процентном соотношении); 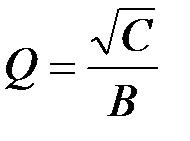 → R 1 или R 2; k → R 4/ R 3.
→ R 1 или R 2; k → R 4/ R 3.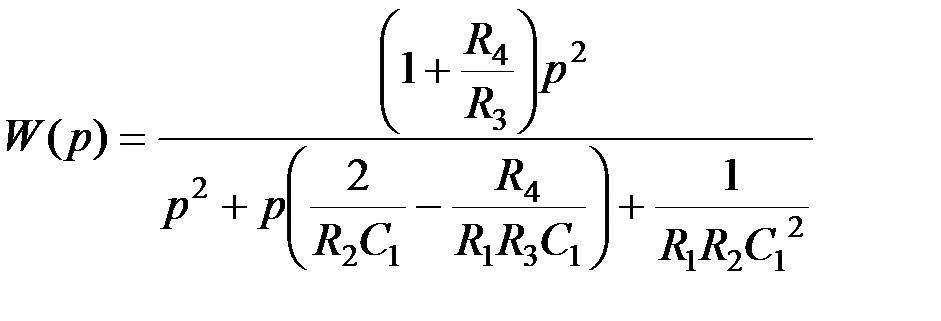 .
.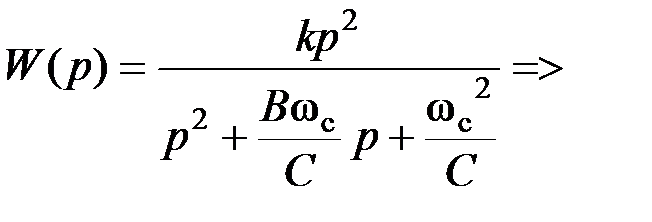
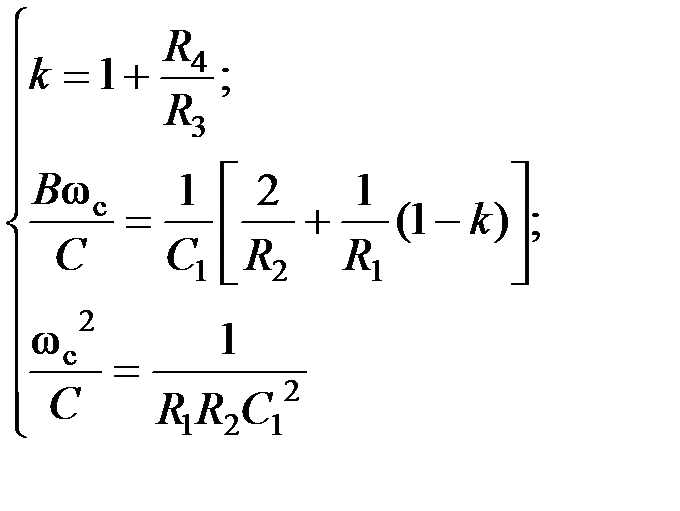
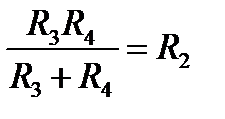 , получаем расчетные соотношения для элементов схемы:
, получаем расчетные соотношения для элементов схемы: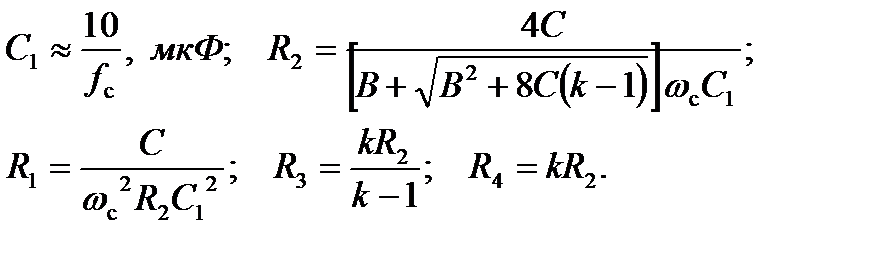
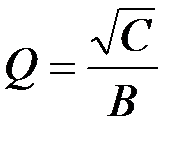 → R 1 или R 2; k → R 4/ R 3.
→ R 1 или R 2; k → R 4/ R 3.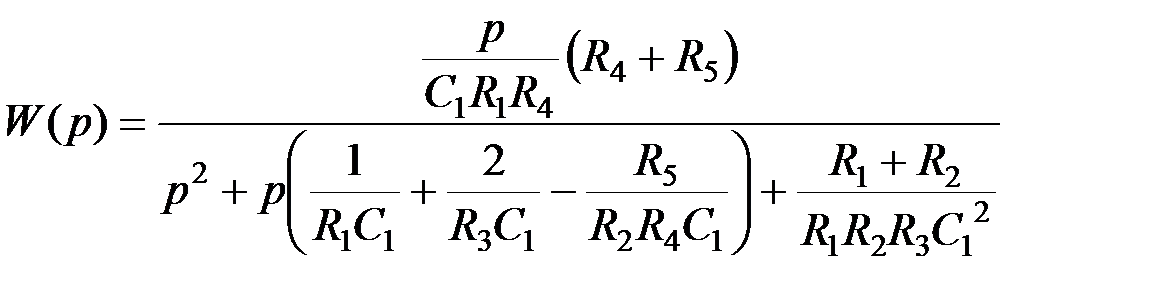 .
.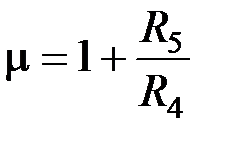 , запишем коэфф-ты передаточной функции ППФ:
, запишем коэфф-ты передаточной функции ППФ: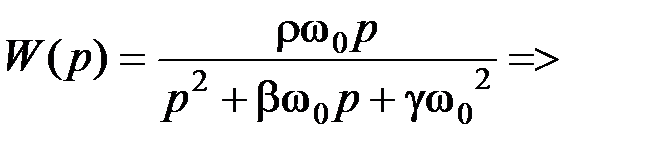
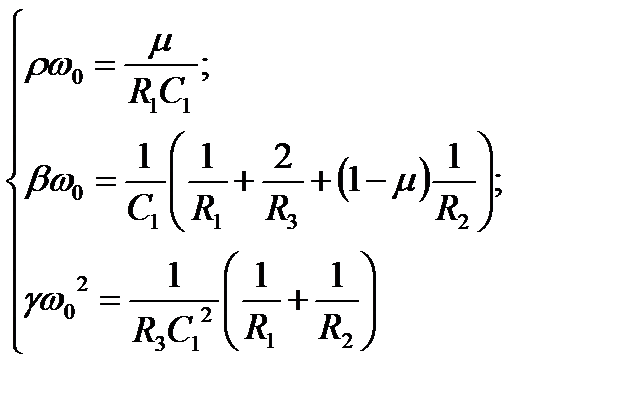
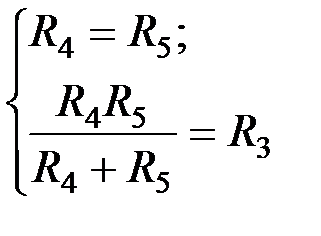
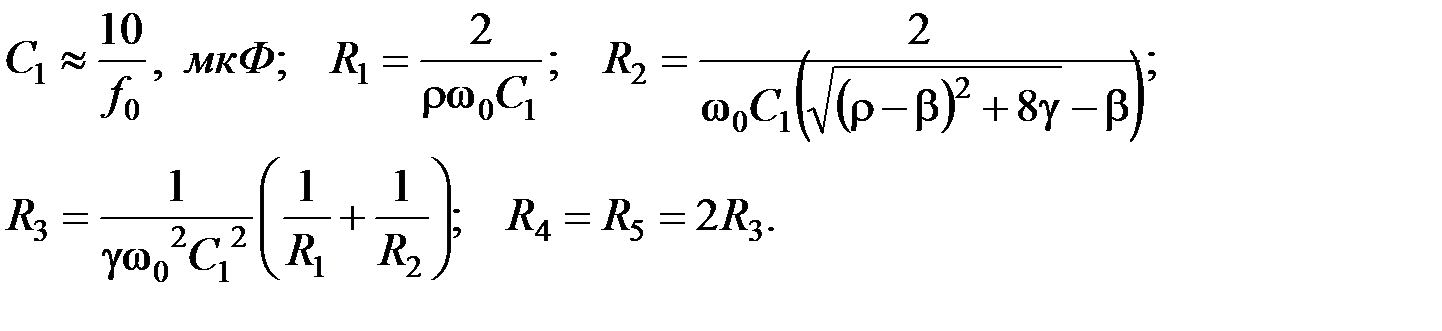
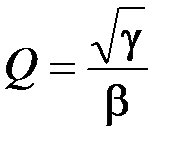 → R 2 или R 3; k → R 1.
→ R 2 или R 3; k → R 1.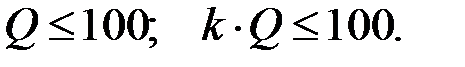
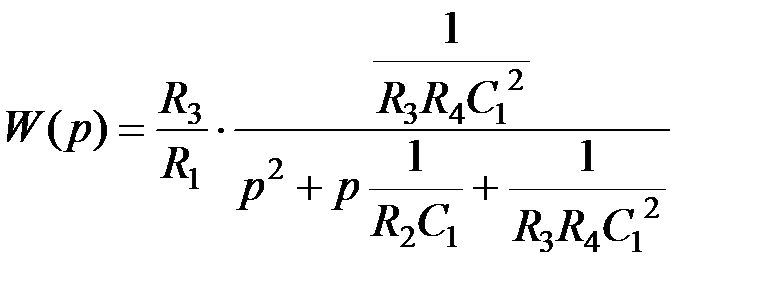 .
.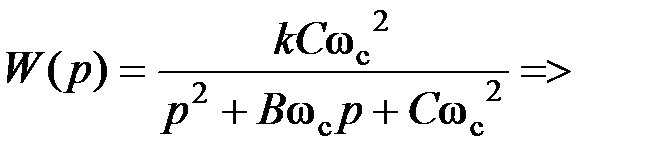
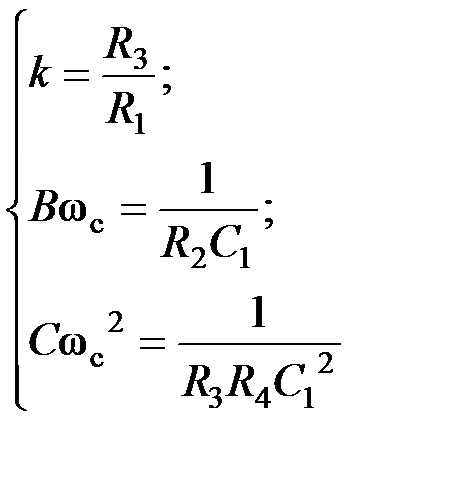
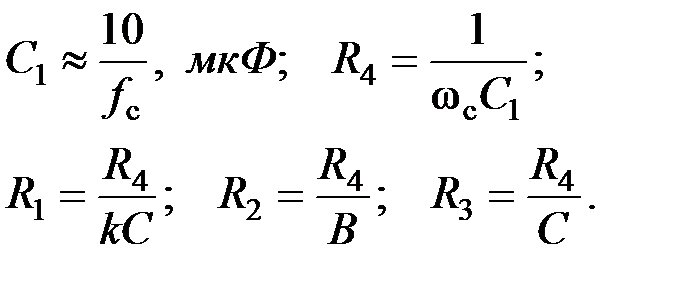
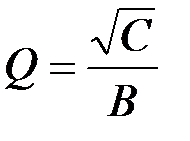 → R 2; k → R 1.
→ R 2; k → R 1.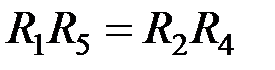 (*),
(*),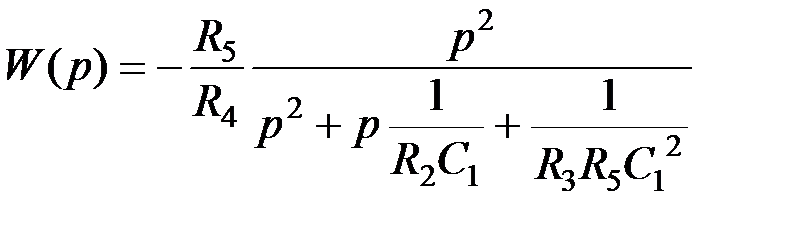 .
.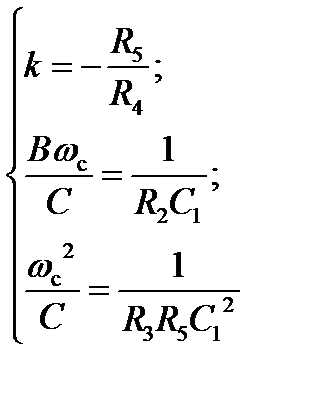 Коэффициенты передаточной функции ФВЧ:
Коэффициенты передаточной функции ФВЧ: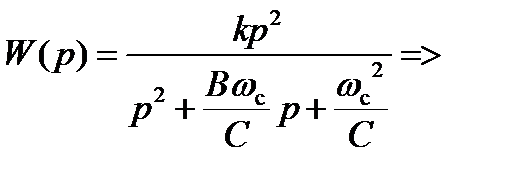
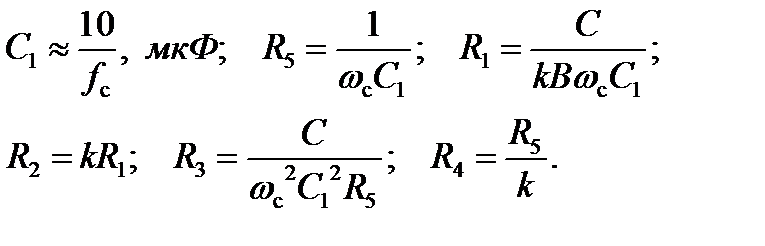
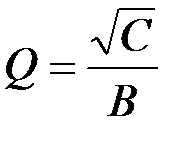 → R 2; k → R 1.
→ R 2; k → R 1.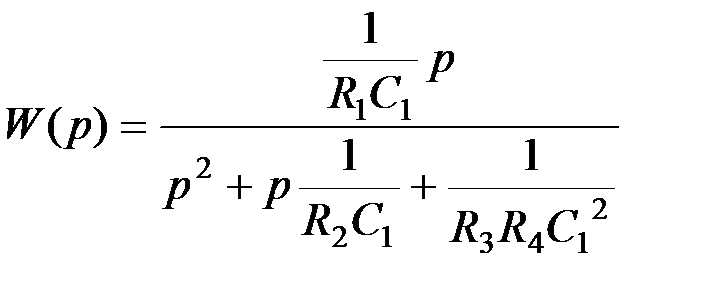 .
.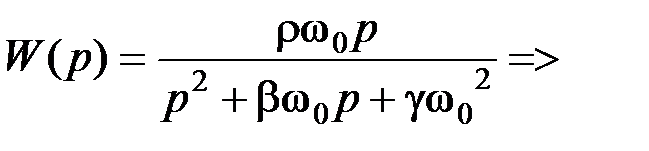
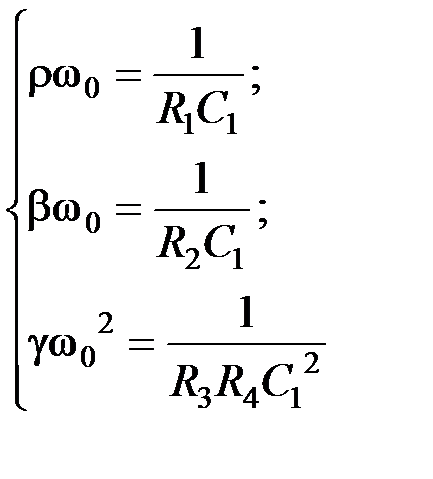
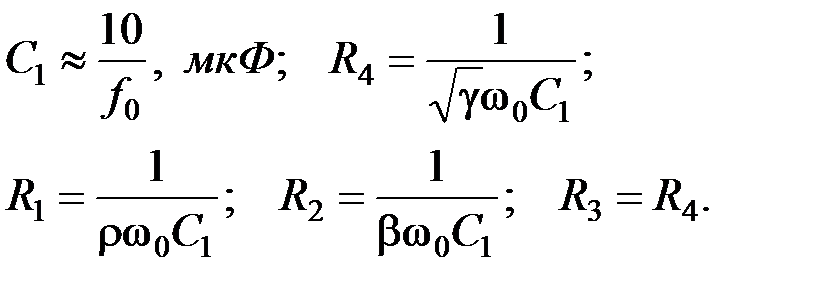
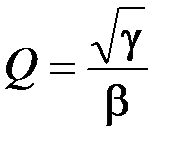 → R 2; k → R 1.
→ R 2; k → R 1.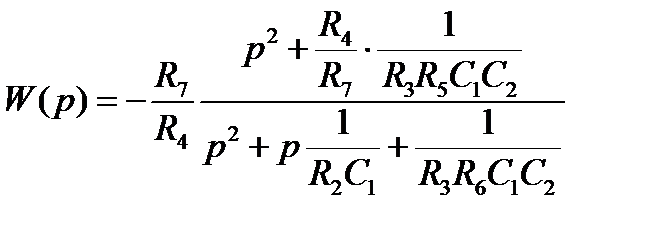 Передаточная функция, соответствующая общему виду передаточной функции неполиномиального звена 2-го порядка:
Передаточная функция, соответствующая общему виду передаточной функции неполиномиального звена 2-го порядка: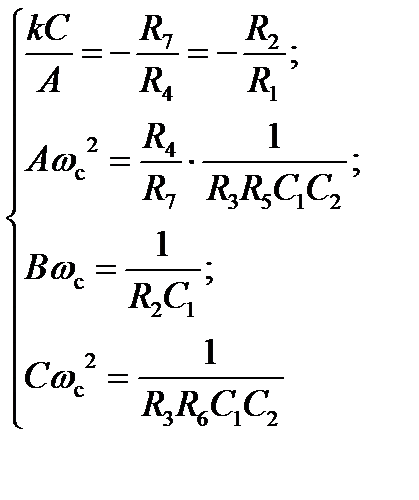 Коэффициенты передаточной функции неполиномиального ФHЧ:
Коэффициенты передаточной функции неполиномиального ФHЧ: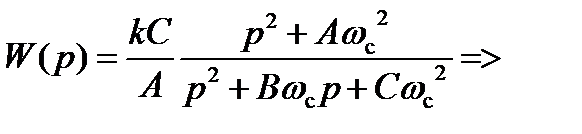
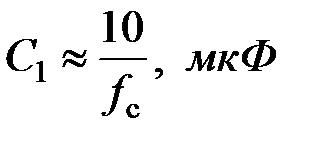 (для всех передаточных функций) При реализации фильтров, имеющих невысокую добротность, емкость C 2 может быть выбрана равной емкости С 1, но в общем случае они могут быть не равны между собой. Значение R 7 выбирается из условия:
(для всех передаточных функций) При реализации фильтров, имеющих невысокую добротность, емкость C 2 может быть выбрана равной емкости С 1, но в общем случае они могут быть не равны между собой. Значение R 7 выбирается из условия: 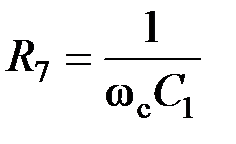 .(для всех передаточных функций)
.(для всех передаточных функций)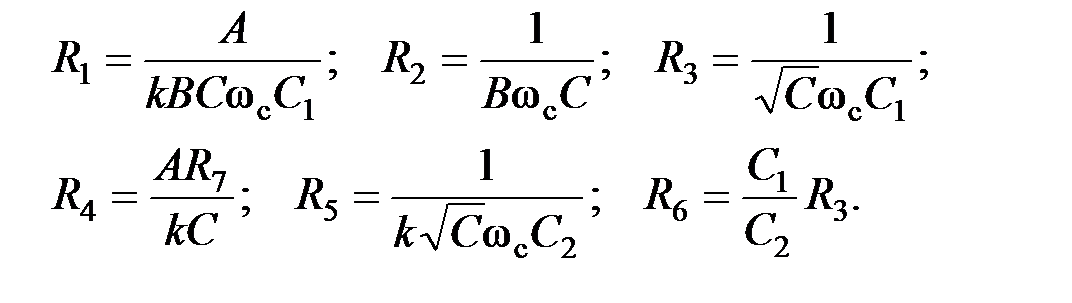
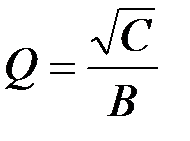 → R 2; k → R 1 или R 5.
→ R 2; k → R 1 или R 5.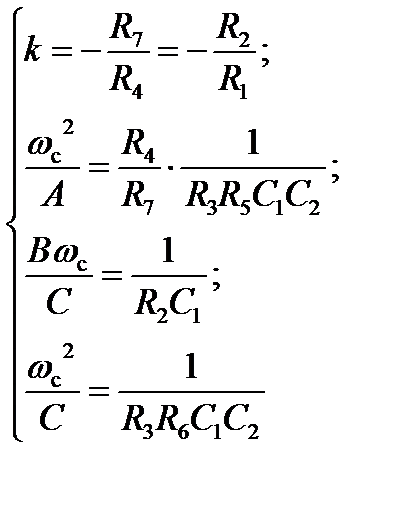 Коэффициенты передаточной функции ФВЧ с неполиномиальным ФНЧ-прототипом:
Коэффициенты передаточной функции ФВЧ с неполиномиальным ФНЧ-прототипом: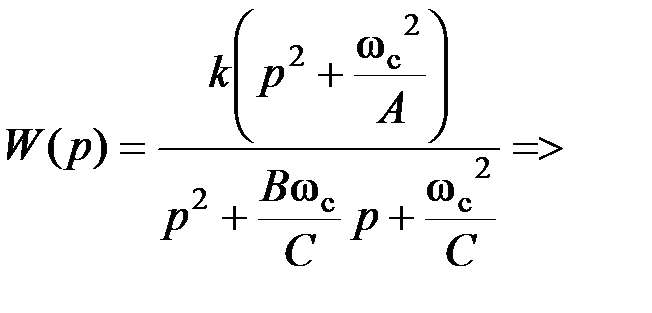
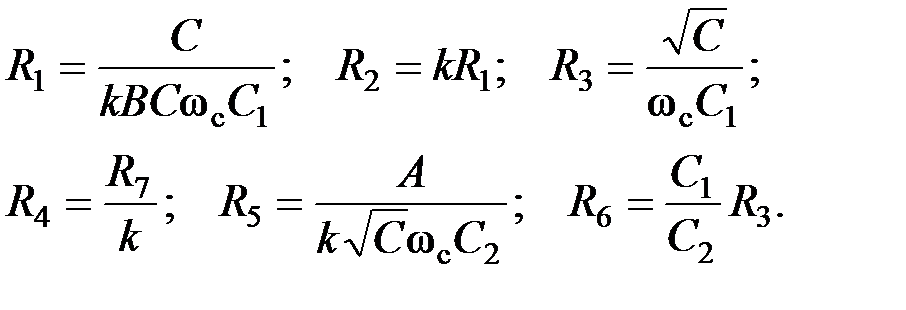
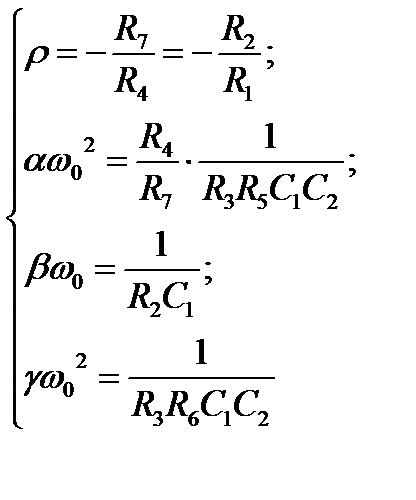 Коэффициенты передаточной функции ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом:
Коэффициенты передаточной функции ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом: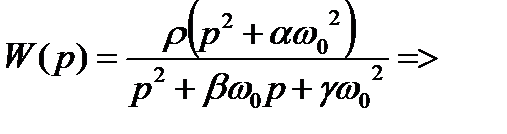
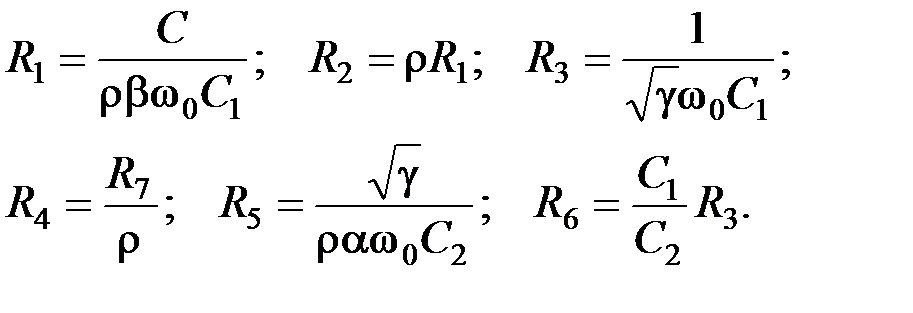
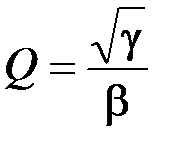 → R 2; r → R 1 или R 5.
→ R 2; r → R 1 или R 5.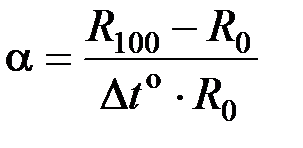 ,
, .
.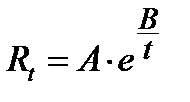 Температурная зависимость сопротивления термометра описывается выражением:
Температурная зависимость сопротивления термометра описывается выражением: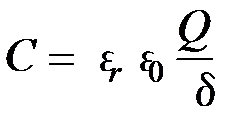 , где ε0 = 8,85 · 10–12 Ф/м – диэлектрическая постоянная; ε r – относительная диэлектр-кая проницаемость среды м/у обкладками; Q – активная площадь обкладок; δ – расстояние м/у обкладками.
, где ε0 = 8,85 · 10–12 Ф/м – диэлектрическая постоянная; ε r – относительная диэлектр-кая проницаемость среды м/у обкладками; Q – активная площадь обкладок; δ – расстояние м/у обкладками.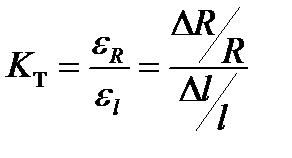 ,где ε R – относительное изменение сопротивления тензорезистора;
,где ε R – относительное изменение сопротивления тензорезистора; 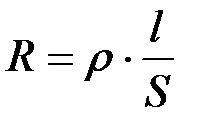 ;
; 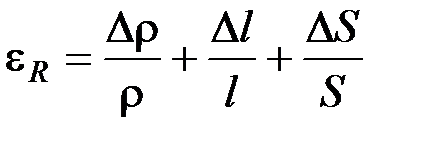 ,
,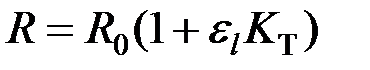 , где R 0 – сопротивление ненагруженного тензорезистора.
, где R 0 – сопротивление ненагруженного тензорезистора.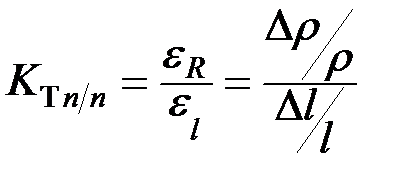 .
. а)
а)
 б)
б)
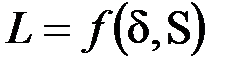 .Индуктивность обмоток, намотанных на каркас вокруг подвижного сердечника, зависит от эффективной длины сердечника l c:
.Индуктивность обмоток, намотанных на каркас вокруг подвижного сердечника, зависит от эффективной длины сердечника l c: 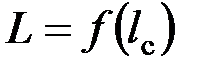 .
.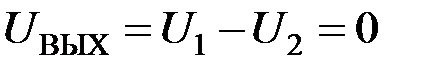 .
.


