
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия устойчивости электронных схемСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Электронная схема является устойчивой если при подаче на вход единичного ступенчатого сигнала, то она возвращается в исходное состояние. Устойчивые схемы имеют переходную характеристику в виду затухающей экспоненты или в виде ступенчатого сигнала. В (таблице 6.1.) приведены переходные характеристики устойчивых электронных схем (первые 4 случая) и неустойчивых схем (нижние 3 случая). Система является устойчивой если корни знаменателя схемной функции будут действительные и отрицательные либо равны нулю либо комплексно-сопряжённые, у которых действительная часть меньше нуля.
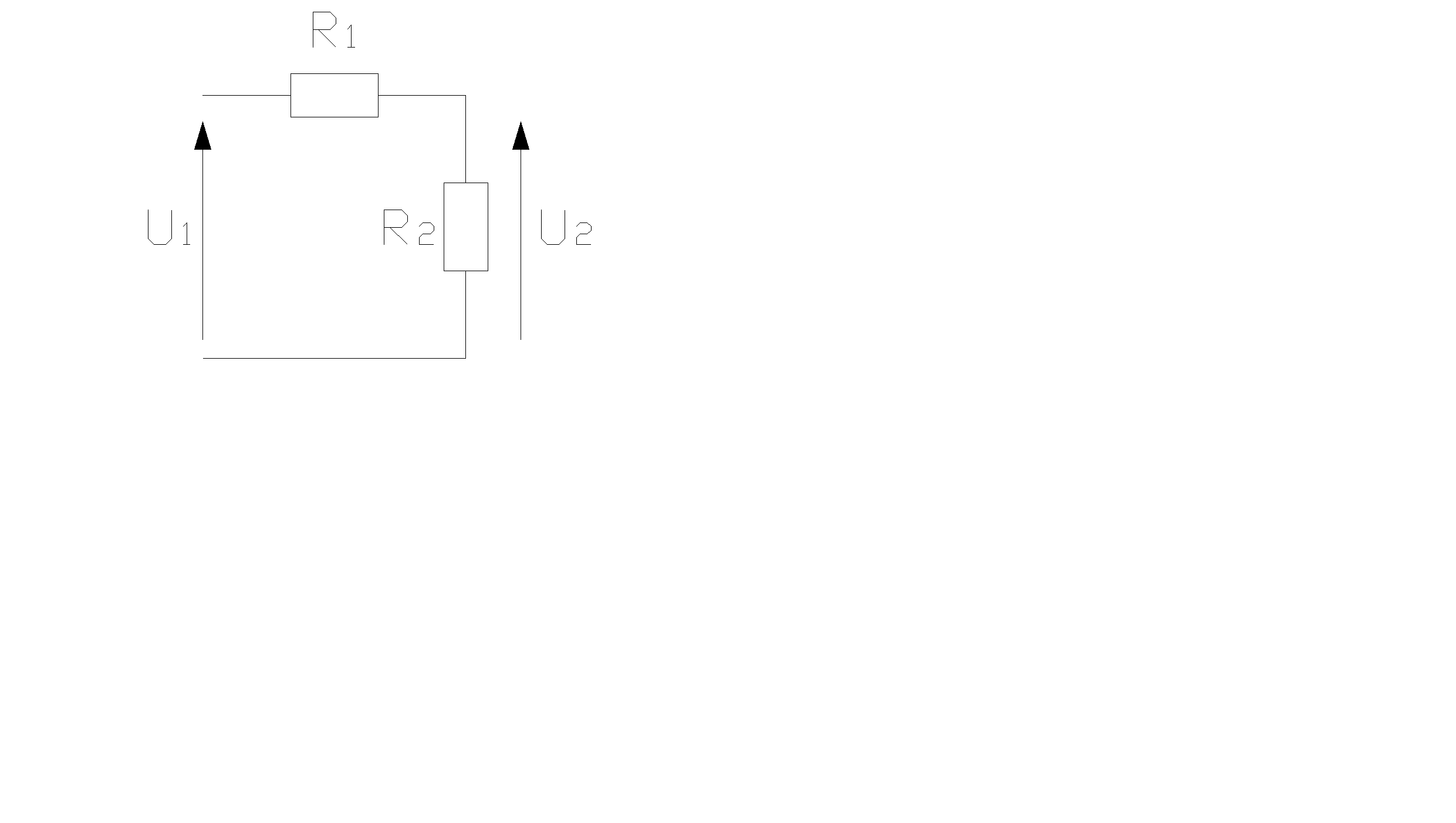
Система будет устойчивой, если полюсы схемной функции расположены либо в левой полуплоскости или в начале координат в плоскости комплексной частоты Система будет неустойчивой, если корни знаменателя будут действительными и положительными либо комплексно-сопряжёнными, у которых Система будет неустойчивой, если полюсы расположены в правой полуплоскости оси Пример: Рис. 2
Электронная схема теряет устойчивость, если Определить устойчивость схем просто, если
Алгебраический критерий устойчивости Рауса-Гурвица Для оценки устойчивости схемы с характеристическим уравнением:
Система устойчива, если: Все коэффициенты ( Все коэффициенты первого столбца таблицы Рауса (6.2.2).
Пример: Определить устойчивость трёх схем с уравнениями:
Частотный критерий устойчивости Михайлова Для оценки устойчивости схемы с характеристическим уравнением (6.3.1) и учётом
Затем задаваясь значением частоты
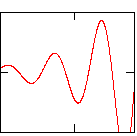
Годограф Михайлова
На рисунке показаны частотные годографы Михайлова устойчивых систем при разных значениях
А) Рис 6.3.1 На практике трудно выбрать частоты 0
Где
Система будет устойчивой, если соблюдается неравенство:
Пример: Определить устойчивость схемы:
Определяем частоты, соответствующие пересечению ГМ с мнимой осью:
Определяем частоты, соответствующие пересечению ГМ с действительной осью:
Учитывая, что
Построим ГМ:
Частотный критерий Найквиста
Данный критерий позволяет судить об устойчивости схем с замкнутой обратной связью по АФХ разомкнутых схем, которую можно получить как аналитически так и экспериментально. Схема устойчивая в разомкнутом состоянии будет устойчива в зависимости, если ГМ при изменении частоты от нуля до
1) 2)
Устойчивые – (1); Не устойчивые – (2) (рис.6.4.1).
Пример: Определить устойчивость замкнутой системы, если возвратное отношение имеет вид:
В разомкнутом состоянии система устойчива. Запишем
Имитансный критерий устойчивости Составляем матрицу проводимостей схемы и определяем входное сопротивление:
Система устойчива, если
Тема 7. Влияние обратных связей на показатели работы электронной схемы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.83 (0.01 с.) |











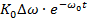




















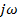 комплексной плоскости. Расположение нулей на этой плоскости не влияет на устойчивость.
комплексной плоскости. Расположение нулей на этой плоскости не влияет на устойчивость.
 – возвратное отношение;
– возвратное отношение;
 . Или
. Или 
 порядка. Можно определить устойчивость не решая (6.1.2) с помощью критерия устойчивости.
порядка. Можно определить устойчивость не решая (6.1.2) с помощью критерия устойчивости.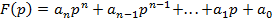 , необходимо составить таблицу Рауса:
, необходимо составить таблицу Рауса:






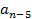


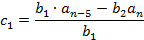
 не равны нулю и имеют одинаковый алгебраический знак;
не равны нулю и имеют одинаковый алгебраический знак;




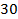

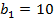





 (0
(0  построим АФХ возвратной разницы (частотный годограф Михайлова). При этом система устойчива, если частотный годограф Михайлова
построим АФХ возвратной разницы (частотный годограф Михайлова). При этом система устойчива, если частотный годограф Михайлова 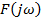 при 0
при 0  последовательно обходит против часовой стрелки
последовательно обходит против часовой стрелки  число квадрантов, начиная при
число квадрантов, начиная при  на действительной оси (
на действительной оси (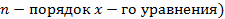 .
.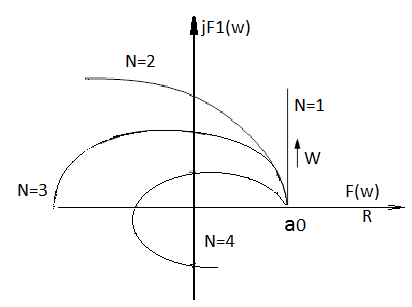


 - частоты, соответствующие пересечению годографа Михайлова с действительной осью, приравнивая мнимую часть к нулю.
- частоты, соответствующие пересечению годографа Михайлова с действительной осью, приравнивая мнимую часть к нулю.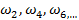 - частоты, соответствующие пересечению годографа Михайлова с мнимой осью, приравнивая действительную часть к нулю.
- частоты, соответствующие пересечению годографа Михайлова с мнимой осью, приравнивая действительную часть к нулю. .
.



 , сделаем вывод – система устойчива.
, сделаем вывод – система устойчива.

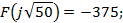


 не охватывает на комплексной плоскости функции
не охватывает на комплексной плоскости функции  , критические точки по пересечению которой являются:
, критические точки по пересечению которой являются:  (рис. 6.4.1.)
(рис. 6.4.1.)





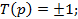 Определяем
Определяем  , при которой частотный годограф пересекает действительную ось, приравняв мнимую составляющую к нулю. После этого найдём
, при которой частотный годограф пересекает действительную ось, приравняв мнимую составляющую к нулю. После этого найдём  . Система будет устойчива, если
. Система будет устойчива, если 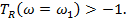

 .
.


