Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Графоаналитический метод анализа электронных схемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 1. Графоаналитический метод анализа электронных схем Общая характеристика и сущность метода Применение метода к анализу электронных схем
Определить статический и динамический режимы работы каскадного усилителя (рис.1.1) в области средних частот, если известно:
В статическом режиме (режиме покоя) определить координаты рабочих точек полевого Для статического режима: Определить все токи, напряжения и мощности рассеивания на всех компонентах схемы, а также максимальную (общую) мощность усилителя. Для динамического режима: Определить токи и напряжения на компонентах схемы, а также все вторичные параметры: коэффициенты усиления по напряжению Статический режим Поставим направления токов и напряжений. Стрелка эмиттера показывает направление тока; ток в затворе несколько нА и им можно пренебречь; Запишем уравнения входных и выходных характеристик цепи транзисторов Уравнение выходной цепи:
Данное уравнение есть уравнением нагрузки по постоянному току. Выразим ток базы через ток стока:
Итак:
Если ток делителя напряжения много больше тока базы, то выражением:
Уравнение входной цепи:
Уравнение (1.2.) есть уравнением линии смещения по постоянному току. Для транзистора
Для входной цепи биполярного транзистора уравнение можно не записывать.
В плоскости выходных характеристик транзистора
Иногда удобней строить линию нагрузки как прямую через точку
По точкам пересечения (а,б,в,г,д) линии нагрузки По
В плоскости выходных характеристик транзистора
Через точки
Учитывая, что
Определим параметры рабочей точки полевого транзистора
Крутизна характеристики (рис. 1.2., в) при
Проводимость при
Определим h-параметры биполярного транзистора исходя из уравнения:
Входное сопротивление при
Коэффициент обратной связи при
Коэффициент усиления по току при
Коэффициент усиления по току при
Определяем мощности рассеивания:
Определим суммарную мощность:
Динамический режим
В динамическом режиме все источники постоянного напряжения закорачиваются, поэтому составляем эквивалентную схему по переменному току. Для полевого транзистора справедливы следующие выражения:
Для биполярного:
Условимся обозначать постоянные токи и напряжения с индексом «0», переменные – с « Запишем уравнения входных и выходных характеристик цепи транзисторов
Запишем уравнения входной цепи транзистора Т1:
Запишем уравнения выходной цепи транзистора Т2:
Запишем уравнения входной цепи транзистора Т2:
В плоскости выходных характеристик транзистора Т2 (рис. 1.2, e) строим линию нагрузки по переменному току ЛН2~ согласно уравнению (1.1.6):
Т.М2~: Т.N2~ : Проводим через М2~ и N2~ ЛН2~ (рис. 1.2, е). Иногда также удобней строить линию нагрузки как прямую через точку Зададимся изменением тока базы:
Строим эпюры токов и напряжений на компонентах схемы. Определяем вторичные параметры усилителя:
Рис. 1.2. Тема 2. Узловой метод анализа электронных схем Тема 3. Метод ориентированных графов Передача графа Можно избежать преобразований графа и записать его передачу по формуле Мезона.
Где n – количество сквозных путей;
r – количество контуров;
Пример: Определить передачу графа (
Пример 2. Определить передачу графа усилителя (рис. 2.), работающего в области средних частот, используя эквивалентные преобразования и формулу Мезона; Запишем уравнения схемной функции
Составим граф схемной функции:
Устраняем вершины:
Устраняем вершину
Устраняем петлю при вершине
Устраняем вершину
Устраняем петлю при вершине
Складываем параллельные ветви и получаем окончательное выражение:
Найдём передачу графа по формуле Мезона: Количество сквозных путей:
Запишем выражения для выходного сопротивления и уравнения причины:
Имея данную систему уравнений, составите соответствующий граф и решаете задачу так, как описано выше.
Тема 4. Определение частотных характеристик и параметров электронной схемы Логарифмический масштаб АЧХ
Декада – это изменение частоты в 10 раз.
Пример 1: Построить АЧХ и ФЧХ схемы с функцией
Графики имеют вид:
Вывод: в АЧХ функции
Пример 2: Построить АЧХ и ФЧХ схемы с функцией
Графики имеют вид:
Пример 3: Построить АЧХ и ФЧХ схемы с функцией
Графики имеют вид:
Пример 4: Построить АЧХ и ФЧХ схемы с функцией
Графики имеют вид:
Пример 5: Построить АЧХ и ФЧХ схемы с функцией
Графики имеют вид:
Пример 6: Построить АЧХ и ФЧХ схемы с функцией
В АЧХ функция Пример 7: Построить АЧХ и ФЧХ схемы с функцией
Графики имеют вид:
Каждый нуль функции даёт положительный наклон 20 дб\дек и максимальный фазовый сдвиг равен
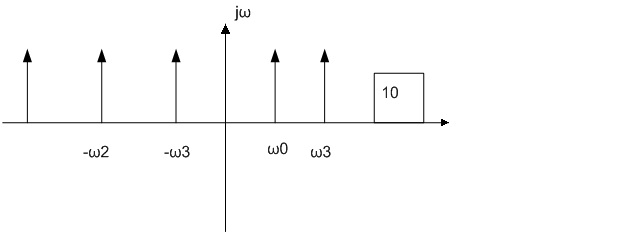
Пример 8: Построить АЧХ схемы с передаточной функцией заданной КОТ:
Годограф Михайлова
На рисунке показаны частотные годографы Михайлова устойчивых систем при разных значениях
А) Рис 6.3.1 На практике трудно выбрать частоты 0
Где
Система будет устойчивой, если соблюдается неравенство:
Пример: Определить устойчивость схемы:
Определяем частоты, соответствующие пересечению ГМ с мнимой осью:
Определяем частоты, соответствующие пересечению ГМ с действительной осью:
Учитывая, что
Построим ГМ:
Метод простых итераций Любую электронную схему в области средних частот можно представить макромоделью (рис. 8.1).
Запишем уравнения
Запишем уравнения
Рис 8.1.1
Алгоритм решения уравнения методом простых итераций:
Выбираем начальное приближение
Вычисляем
Вычисляем
Продолжаем выполнять эти действия пока не выполнится условие в п.3.
Пример: Определить токи и напряжения, статическое и динамическое сопротивление на нелинейном элементе методом простых итераций в схеме (рис.8.1, а) если известно:
Составим таблицу:
Найденный ток
Определяем напряжения на компонентах схемы:
Определим статическое и динамическое сопротивление:
Данный метод имеет недостатки:
Относительно большое количество итераций;
Иногда низкая сходимость результатов.
Метод Ньютона – Рапсона
Запишем функцию
Алгоритм аналогичен методу простых итераций.
Тема 1. Графоаналитический метод анализа электронных схем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.013 с.) |




 и биполярного транзисторов
и биполярного транзисторов  . Параметры рабочей точки
. Параметры рабочей точки  : Крутизна характеристики
: Крутизна характеристики  , Проводимость канала
, Проводимость канала  ; Параметры рабочей точки
; Параметры рабочей точки  : Входное сопротивление
: Входное сопротивление  , обратный коэффициент передачи по напряжению
, обратный коэффициент передачи по напряжению  , коэффициент усиления по току
, коэффициент усиления по току 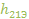 , выходная проводимость
, выходная проводимость  .
. , по току
, по току  и по мощности
и по мощности  , входное
, входное  и выходное
и выходное  сопротивления.
сопротивления. усилителя (
усилителя ( 
 . Для транзистора
. Для транзистора  в схеме (рис.1.1.):
в схеме (рис.1.1.):


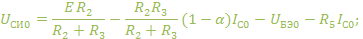
 можно пренебречь. Получим окончательное уравнение:
можно пренебречь. Получим окончательное уравнение:

 уравнение выходной цепи:
уравнение выходной цепи:



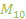 под углом
под углом  .
. с выходными характеристиками транзистора
с выходными характеристиками транзистора 

 согласно уравнению (1.1.3.) по точкам:
согласно уравнению (1.1.3.) по точкам:

 и
и  проводим
проводим  .
.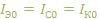 , запишем координаты рабочих точек транзисторов:
, запишем координаты рабочих точек транзисторов:
 .
.
 :
:
 :
:
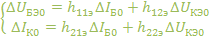
 :
:
 :
:






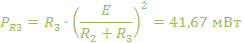







 » или с «
» или с « », а мгновенные значения – с «’».
», а мгновенные значения – с «’». (1.1.4)
(1.1.4)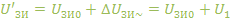 (1.1.5)
(1.1.5) (1.1.6)
(1.1.6)



 под углом
под углом  ;
;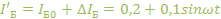







 – передача
– передача  – го сквозного пути;
– го сквозного пути;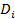 – дополнение
– дополнение 



 ) системы (рис. 1):
) системы (рис. 1):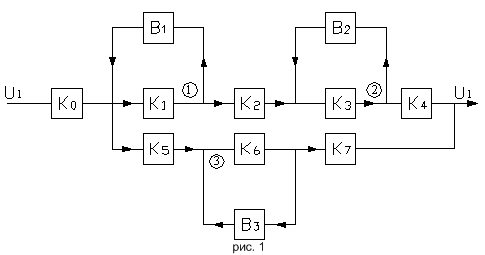




 .
. :
:





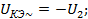

 :
:








 Количество контуров:
Количество контуров:  ;
;







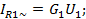









 представляют собой прямую, пересекающую ось частот (уровень 0 дБ) и имеющую положительный наклон – 20
представляют собой прямую, пересекающую ось частот (уровень 0 дБ) и имеющую положительный наклон – 20  .
.





















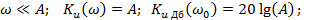
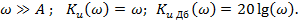
 аппроксимируют 2-мя отрезками на частотах меньше
аппроксимируют 2-мя отрезками на частотах меньше  в линии с нулевыми значениями, а при частотах больше
в линии с нулевыми значениями, а при частотах больше 




 , а каждый корень знаменателя даёт отрицательный наклон АЧХ -20 дб\дек и максимальный фазовый сдвиг
, а каждый корень знаменателя даёт отрицательный наклон АЧХ -20 дб\дек и максимальный фазовый сдвиг 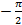 .
.


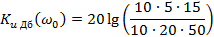
 . (6.3.1, а,б)
. (6.3.1, а,б)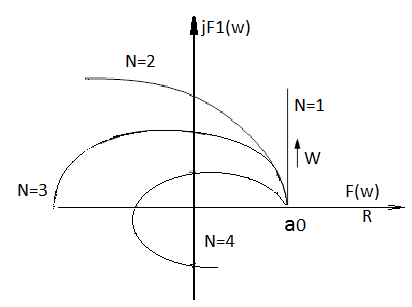

 . (Рис. 6.3.2)
. (Рис. 6.3.2)
 - частоты, соответствующие пересечению годографа Михайлова с действительной осью, приравнивая мнимую часть к нулю.
- частоты, соответствующие пересечению годографа Михайлова с действительной осью, приравнивая мнимую часть к нулю.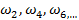 - частоты, соответствующие пересечению годографа Михайлова с мнимой осью, приравнивая действительную часть к нулю.
- частоты, соответствующие пересечению годографа Михайлова с мнимой осью, приравнивая действительную часть к нулю. .
.



 , сделаем вывод – система устойчива.
, сделаем вывод – система устойчива.

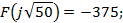

 го закона Кирхгофа для схемы а):
го закона Кирхгофа для схемы а):

 го закона Кирхгофа для схемы б):
го закона Кирхгофа для схемы б):


 ;
; и проверяем разность;
и проверяем разность; ;
; и проверяем разность;
и проверяем разность;
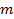



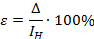
















 равен:
равен:  .
.
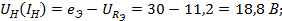



 в окрестности точки
в окрестности точки  . Разложим в ряд Тейлора
. Разложим в ряд Тейлора